Cube Roots
Basics on the topic Cube Roots
What is a Cube Root?
Think of cube roots as a math adventure where you're exploring the world of numbers in 3D, just like how video games have 3D worlds. Cube roots pop up in subjects like algebra and geometry, and you'll even see them in real life, like when figuring out how much soil you need for a garden box or how much space there is inside a large box.
A cube root of a number is a value that, when multiplied by itself three times (cubed), gives that original number.
For example, the cube root of $27$ is $3$ because $(3)(3)(3) = 27$. Cube roots are denoted as $\sqrt[3]{x}$, where $x$ is the number you find the cube root of.
A cubed number means that the exponent is $3$, and another way to say it is to the third power. To review this concept, check out this video: Exponents.
Understanding Cube Roots – Explanation
There are two main ways of finding cube roots.
- Prime Factorization Method: This involves breaking down a number into its prime factors and grouping them into sets of three. The product of these sets is equal to the cube root.
- Estimated Guess and Check Method: In the Estimated Guess and Check Method, start by guessing a number that could be the cube root of your target number. Then, cube your guess (n3) and see if it matches the original number. If it doesn't, adjust your guess based on whether it was too high or too low, and try again. Keep refining your guess until you find the right cube root.
Perfect Cubes
Perfect cubes are integers that can be obtained by cubing another integer. For example, $8$ is a perfect cube because it's 23.
Perfect Cube Examples
| Number (n) | Cube (n3) |
|---|---|
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
| 4 | 64 |
| 5 | 125 |
Here is a cube with side lengths that are each 5 units, and since 53 is 125, that is the total volume. Therefore, the cube root of 125 is 5.
Cube Roots – Guided Practice
To get a better understanding of exponents, this video can teach you all you need to know about Exponential Notation.
Cube Roots – Exercises
Find the solution on your own!
If you are interested in learning more about a different type of roots, square roots, this video is helpful: Simplifying Radical Expressions.
Cube Roots – Summary
Cube roots are an essential concept in mathematics, representing the inverse operation of cubing a number.
- Cube roots are the inverse of cubing a number.
- They can be found using prime factorization or guess and check.
- Perfect cubes are numbers that are the cube of an integer.
- Exponential notation is helpful in calculating cube roots.
Cube Roots – Frequently Asked Questions
Transcript Cube Roots
Imagine you need to find the dimensions of a cube that contains three thousand three hundred seventy-five cubes. One way to answer the question is to find a number's cube root. A cube root is a number that, when multiplied by itself three times, equals a given number. You can find the cube root of any number, but only a perfect cube root will have a solution that is an integer. The cube root symbol is similar to the square root symbol, but it has a three here. Before we answer the opening question, let's learn how to find the cube root of some smaller numbers, such as twenty-seven. One strategy is to use trial and error to find out what number multiplied by itself three times would equal twenty-seven. But, there is a more efficient strategy to calculate a cube root, and it's something you probably already know how to do prime factorization! We know that nine times three is twenty-seven. Three times three is nine, which is where we stop since we only have prime factors. Looking at our prime factors, we notice that we have three threes. Three to the third power is equal to twenty-seven. The cube root of twenty-seven is three. Now, find the cube root of one hundred twenty-five by using prime factorization to find a group of three matching prime numbers. The prime factors of one hundred twenty-five are shown here. There are three fives which are the prime factors, therefore five is the solution. Let's take a look at a more challenging example, find the cube root of one thousand seven hundred twenty-eight. When we prime factorize this number, we end up with a group of three twos, three more twos, and three threes. Here we have a different way of writing this value, but the prime factors are grouped together in grouping symbols, and then cubed. The product of these prime factors is twelve, which is then the cube root of one thousand seven hundred twenty-eight. Pause the video to find the cube root of two hundred sixteen on your own. Let's take a look a look at the prime factors of two hundred sixteen. The prime factors are three twos and three threes. Two cubed multiplied by three cubed is equal to two hundred sixteen. One value from each group of three will represent that prime factor, and then the product of those can be found. The product of two and three is six, which is the cube root of two hundred sixteen. Let's summarize. All numbers have a cube root, which is a number that, when multiplied by itself three times, equals a given number. One strategy to find the cube root of a perfect cube is to use prime factorization, and then create groups of three matching prime numbers. To find the cube root, we will find the product of one representative from each group of prime numbers. Finding the cube root is an important skill when it comes to problem-solving with volume, like finding the dimensions of a cube. And speaking of finding the dimensions of a cube, let's get back to that cube we started with! Three thousand three hundred seventy-three, three thousand three hundred seventy-four, three thousand three hundred seventy-five! See if you can find the cube root of this number and share it in the comments!
Cube Roots exercise
-
Complete the description of cube roots.
HintsWhen finding the cube root, do we look for a number that adds to or multiplies by itself? How many times?
This is the square root symbol ${\sqrt{}}$. What do we add to make it the cube root symbol?
Look at the image, we use this method to help us find the cube root. What is the method called?
SolutionA cube root is a number that, when multiplied by itself three times, equals a given number.
The mathematical symbol for the cube root of a number looks like the mathematical symbol for the square root of a number with an additional 3. It looks like this, ${\bf{\sqrt[3]{ }}}$.
We use prime factorization to help us find the cube root of a number.
-
Identify the cube root of a number
HintsA cube root is a number that, when multiplied by itself three times, equals a given number.
We can use prime factorization to find the cube root. In the image we can see how that is used to find the cube root of $125$.
Cubes and cube roots are inverse operations (opposites). $5$ cubed is equal to $125$, therefore the cube root of $125$ is ...
Solution$27 = 3 \times 3 \times 3$ so the cube root of $\bf{27}$ is $\bf{3}$.
$125 = 5 \times 5 \times 5$ so the cube root of $\bf{125}$ is $\bf{5}$.
$8 = 2 \times 2 \times 2$ so the cube root of $\bf{8}$ is $\bf{2}$.
$1 = 1 \times 1 \times 1$ so the cube root of $\bf{1}$ is $\bf{1}$. -
Identify the cube roots
HintsWe can use prime factorization to find the cube root of a number. For example, if we were finding the cube root of $27$ then $27 = 3 \times 3 \times 3$.
Cubes and cube roots are inverse operations (opposites) if you know that $3^3=27$ then you know that the cube root of $27$ is $3$.
Solution- $1000 = 2 \times 2 \times 2 \times 5 \times 5 \times 5 = (2 \times 5)(2 \times 5)(2 \times 5) = 10 \times 10 \times 10 = 10^3$ so, $\bf{\sqrt[3]{1,000} =10}$.
- $343= 7 \times 7 \times 7 = 7^3$ so, $\bf{\sqrt[3]{343} =7}$.
- $216 = 2 \times 2 \times 2 \times 3 \times 3 \times 3 = (2 \times 3) \times (2 \times 3) \times (2 \times 3) = 6 \times 6 \times 6 = 6^3$ so, $\bf{\sqrt[3]{216} =6}$.
- $729 = 9 \times 9 \times 9 = 9^3$ so, $\bf{\sqrt[3]{729} =9}$.
-
Use prime factorization to find the cube root of a larger number.
HintsFind the prime factorization - this is a large number so you will want to notice that even numbers can be divided by $2$ first.
Do you know your divisibility rules? For example if a number can be divided by $3$ the sum of the digits is divisible by $3$.
$2 + 7 + 4 + 4 = 17$, $17$ is not divisible by $3$ so $2{,}744$ is not divisible by $3$ either.
$2{,}744 = 2 \times 2 \times 2 \times 7 \times 7 \times 7$
Solution$2{,}744 = 2 \times 2 \times 2 \times 7 \times 7 \times 7 = 2 \times 7 \times 2 \times 7 \times 2 \times 7 = (2 \times 7) \times (2 \times 7) \times (2 \times 7) = 14 \times 14 \times 14 = 14^3$
Therefore $\bf{\sqrt[3]{2{,}744}}$ = $14$.
-
What is the $\sqrt[3]{64}$?
HintsWhat is the prime factorization of $64$?
$64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2$
We need three groups of numbers so we can rearrange this to show
$64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = (2 \times 2) \times (2 \times 2) \times (2 \times 2) = 4 \times 4 \times 4$Solution$64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2$
$2 \times 2 \times 2 \times 2 \times 2 \times 2 = (2 \times 2) \times (2 \times 2) \times (2 \times 2) = 4 \times 4 \times 4$
$4 \times 4 \times 4 = 4^3$
The $\sqrt[\bf{3}]{\bf{64}}$ is $\bf{4}$. -
Identify numbers that are a perfect cube.
HintsA perfect cube root will have a solution that is an integer (whole number).
$300 = 2 \times 2 \times 3 \times 5 \times 5$, this cannot be rearranged into three identical groups so $\bf{300}$ does not have a perfect cube root.
Another way we know that $300$ does not have a perfect cube root is by looking at the perfect cubes either side of it.
$6 \times 6 \times 6 = 216$
$7 \times 7 \times 7 = 343$
$300$ is between $216$ and $343$ so the cube root of $\bf{300}$ is greater than $\bf{6}$ but less than $\bf{7}$ . It cannot be an integer answer and therefore does not have a perfect cube root.Solution$\bf{343}$, $\bf{1{,}331}$, and $\bf{3{,}375}$ are perfect cubes.
- $343 = 7 \times 7 \times 7$ so $343$ has a perfect cube root.
- $1{,}331 = 11 \times 11 \times 11$ so $1{,}331$ has a perfect cube root.
- $3{,}375 = 15 \times 15 \times 15$ so $3{,}375$ has a perfect cube root.
$\bf{3{,}00}$, $\bf{3{,}000}$ and $\bf{3{,}300}$ are not perfect cubes.
- $300 = 2 \times 2 \times 3 \times 5 \times 5$ so $300$ does not have a perfect cube root.
- $3{,}300 = 33 \times 100 = 2 \times 2 \times 3 \times 5 \times 5 \times 11$ so $3{,}300$ does not have a perfect cube root.
- $3{,}000 = 2 \times 2 \times 2 \times 3 \times 5 \times 5 \times 5$ so $3{,}000$ does not have a perfect cube root.

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
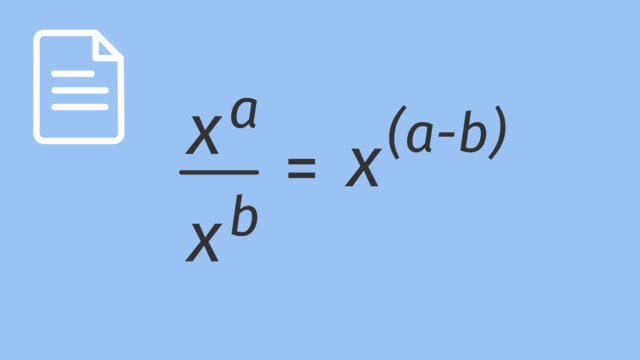
Division with Exponents
How to Convert Decimals Expansions
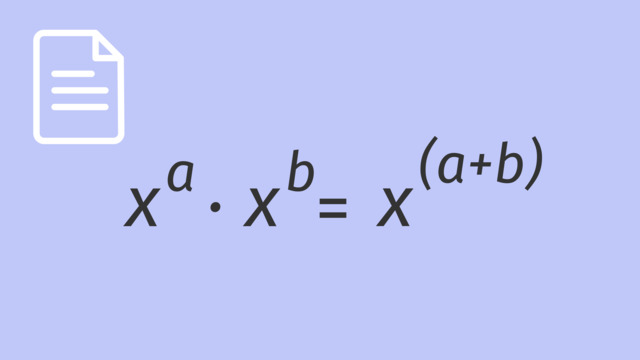
Multiplication with Exponents
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems













