Simplifying Fractions
Learning text on the topic Simplifying Fractions
Simplifying Fractions
Simplifying fractions is a fundamental skill in mathematics. This concept helps in understanding fractions better and preparing you for more advanced mathematical operations involving fractions, such as when adding and subtracting fractions with unlike denominators.
Fraction simplification is when we reduce fractions into their simplest form.
Let’s learn how to create simplified fractions!
Simplifying Fractions – Rules
Simplifying fractions involves reducing them to their simplest form. This process makes fractions easier to understand and work with. We can refer to these fractions as simplest form fractions. Below, you will find the fraction simplification rules.
| Rule | Description |
|---|---|
| Identify the GCF | Find the greatest common factor of the numerator and denominator. |
| Divide by GCF | Divide both the numerator and the denominator by the GCF. |
| Write Simplified Fraction | Write the new values as the simplified fraction. |
| Check if Already Simplest Form | If there are no common factors, the fraction is already in its simplest form. |
Definition: Simplifying Fractions is the process of reducing the numerator and denominator of a fraction to their smallest possible values while keeping the fraction equivalent to the original.
Simplifying Fractions – Example
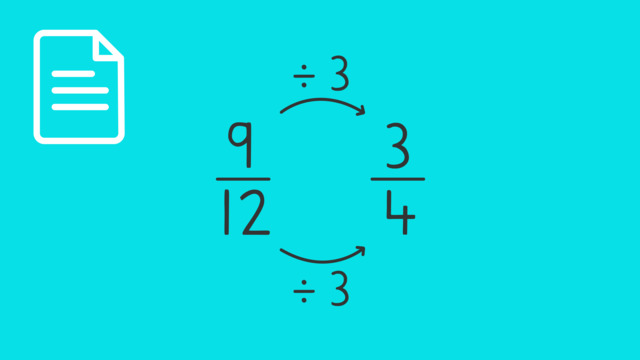
Let's simplify the fraction $\frac{9}{12}$.
First, list the factors of both the numerator, 9, and the denominator, 12.
The factors of 9 are 1, 3, and 9. The factors of 12 are 1, 2, 3, 4, 6, and 12.
Then find the greatest common factor (GCF) they both share. In this case, it is 3.
Divide both the numerator and the denominator by 3.
This means that $\frac{9}{12}$ simplifies to $\frac{3}{4}$.
Before moving ahead, check your understanding of the learning so far by using the following questions:
Simplifying Fractions – Guided Practice
Let’s work through the following question together. Let’s simplify $\frac{16}{24}$.
Simplifying Fractions – Exercises
Here are some simplifying fractions practice questions for you to have a go at yourself. Review the steps in the rules table if you need to!
Simplifying Fractions – Summary
- Simplifying fractions makes them easier to understand and work with.
- The process involves finding the greatest common factor of the numerator and denominator and dividing both by this number.
- Simplified fractions are equivalent to the original fraction but in their simplest form.
Explore more about fractions and other math concepts through our interactive tools, videos, and printable worksheets to enhance your learning journey!
If you need some extra support with this topic, why not check out the learning text on Equivalent Fractions.
If you’re feeling confident and ready for some practicing using you new fraction skills, then check out the learning text on Comparing Fractions.
Frequently Asked Questions – Simplifying Fractions
Simplifying Fractions exercise
-
How do we simplify a fraction?
HintsWhen simplifying a fraction we can only divide the numerator and denominator by the same number, or it will not have the same value. For example:
When the fraction is simplified we should check if there are no more common factors.
If there are not then the fraction is fully simplified.
Solution- Find the highest common factor of the numerator and denominator.
- Divide both the numerator and the denominator by the HCF.
- Write the new values as the simplified fraction.
- If there are no more common factors, the fraction is finally in its simplest form.
-
Simplify the fractions.
HintsFind the HCF of the numerator and the denominator.
Divide them by the HCF.
Check there are no more factors which are common.
When simplifying $\frac{3}{9}$ we would find the factors of $3$ and $9$.
Factors of $3$ are $1$ and $3$.
Factors of $9$ are $1$, $3$, $9$.
HCF is $3$ so we divide numerator and denominator by $3$.
Solution- $\mathbf{\dfrac{3}{9}}$ = $\mathbf{\dfrac{1}{3}}$
- $\mathbf{\dfrac{4}{16}}$ = $\mathbf{\dfrac{1}{4}}$
- $\mathbf{\dfrac{6}{9}}$ = $\mathbf{\dfrac{2}{3}}$
- $\mathbf{\dfrac{13}{26}}$ = $\mathbf{\dfrac{1}{2}}$
The method for each fraction:
- Find the factors of the numerator and the denominator.
- Choose the HCF (the highest common factor).
- Divide them by the HCF.
- Check there are no more factors that are common.
-
Find the percentage of watermelon in a fruit salad.
HintsThe fraction of melon is $\frac{150}{300}$.
How can we simplify this?
Find all the factors of $150$ and all the factors of $300$.
Find the HCF and divide by this.
The HCF of $150$ and $300$ is $150$.
Divide the numerator and the denominator by $150$.
Solution$\mathbf{\frac{1}{2}}$
Here are some of the factors of $150$
$1$, $5$, $25$, $150$,.......
Here are some of the factors of $300$.
$1$, $2$, $3$, $5$, $25$, $100$, $150$,.....
We can see that $150$ is the HCF.
Divide the numerator and denominator by $150$.
-
Fraction Match!
HintsWe do these the same way although the numbers are bigger.
The factors of $12$ are $1$, $2$, $3$, $4$, $6$ and $12$
Some of the factors of $72$ are $1$, $2$, $6$ and $12$ .....
The HCF is $12$.
Divide by this.
The HCF is $24$.
We divide the numerator and denominator by this.
Solution$\mathbf{\frac{22}{44}}$ = $\mathbf{\frac{1}{2}}$ (divided by $22$)
$\mathbf{\frac{15}{45}}$ = $\mathbf{\frac{1}{3}}$ (divided by $15$)
$\mathbf{\frac{24}{96}}$ = $\mathbf{\frac{1}{4}}$ (divided by $24$)
$\mathbf{\frac{12}{72}}$ = $\mathbf{\frac{1}{6}}$ (divided by $12$)
We find the HCF of each and divide the numerator and denominator by this.
-
Simplify the fraction.
HintsList the factors of the numerator and the denominator. This will make spotting the HCF easier.
For example, factors of $12$ are $1$, $2$, $3$, $4$, $6$, $12$.
Find the HCF of the numerator and the denominator and divide by this number. For example:
Solution$\mathbf{\frac{4}{5}}$
List the factors of $12$ ($1$, $2$, $3$, $4$, $6$, $12$)
List the factors of $15$ ($1$, $3$, $5$, $15$)
HCF is $3$
Divide the numerator and denominator by $3$.
-
Simplify a fraction to solve the problem.
HintsWe are looking for the amount of money Luke has left!
We must subtract first.
$56$ - $14$ spent = $42$.
Once we have subtracted the money spent at the cinema, it leaves the fraction $\frac{42}{56}$.
We can now find the HCF and divide the numerator and denominator by it to simplify the fraction.
SolutionThe correct answer is $\mathbf{\frac{3}{4}}$
$56$ - $14$ = $42$
Fraction is $\frac{42}{56}$
Factors of $42$ are $1$, $2$, $3$, $7$, $14$.
Factors of $56$ are $1$, $2$, $4$, $7$, $8$, $14$, $28$, $56$.
HCF = $14$
We divide the numerator and the denominator by $14$.

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
Division with Exponents
How to Convert Decimals Expansions
Multiplication with Exponents
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems










