Equivalent Fractions
Learning text on the topic Equivalent Fractions
Equivalent Fractions
Equivalent fractions are a fundamental concept in mathematics. They are fractions that, though they might look different, actually represent the same value. Understanding equivalent fractions is essential for working with trickier math problems, such as adding and subtracting fractions, where fractions need to have the same denominators. Let’s explore what equivalent fractions are, and how we can find equivalent fractions!
Understanding Equivalent Fractions
Equivalent fractions are pairs or groups of fractions with different numerators and denominators that represent the same part of a whole. For example, $\frac{1}{2}$ and $\frac{2}{4}$ are equivalent fractions.
There are two ways to find equivalent fractions:
One way of finding equivalent fractions, as we see above, is to create visual representations of the fractions and compare them. When you do this, you must use the same size bar or circle to ensure your models are accurate. Then, you can compare them together to see if they are equivalent or not.
Another way to find equivalent fractions, is to multiply or divide the numerator and denominator of a fraction by the same non-zero number.
For example, if we multiply the numerator and denominator of $\frac{3}{6}$ by three, we get an equivalent fraction of $\frac{9}{18}$.
Remember, the numerator is the top number of a fraction, indicating how many parts are taken, and the denominator is the bottom number, showing the total number of parts in a whole.
Let’s check your understanding so far with some quick questions!
Equivalent Fractions – Guided Practice
Let’s practice finding equivalent fractions together using $\frac{3}{5}$. For this example, let’s find an equivalent fraction with a denominator of 15. In this instance, we know we need to multiply the denominator, 5, by 3 to get 15. We would also need to do the same to the numerator.
Equivalent Fractions – Exercises
Equivalent Fractions – Summary
Equivalent fractions are different fractions that represent the same value. There are two ways you can find equivalent fractions:
- To find an equivalent fraction, multiply or divide both the numerator and denominator by the same number.
- Create visual models of given fractions and then compare them to see if they are equivalent.
Knowing how to calculate or find equivalent fractions is helpful when adding or subtracting fractions with different denominators.
Explore more about fractions, such as how to Generate Equivalent Fractions and other fraction topics through interactive practice problems, engaging videos, and printable worksheets on our educational platform. Enhance your learning journey with these resources!
If you feel like you need extra practice, then review Equivalent Fractions. After, come back and have another go at the problems on this page.
Equivalent Fractions – Frequently Asked Questions
Equivalent Fractions exercise
-
What is the correct notation?
HintsThe number on the top of the fraction indicates how many parts are taken.
The number on the bottom of the fraction shows the number of total parts in the whole.
For example, $\frac{1}{2}$ means $1$ part out of $2$ total parts.
The fraction notation words are Numerator and Denominator. One of them is the number of parts and belongs at the top and one is the total parts and belongs on the bottom.
As an example we can see the shaded parts out of the total parts.
Solution$\mathbf{\frac{Numerator}{Denominator}}$
Numerator indicates how many parts are taken.
Denominator shows the number of total parts in the whole.
-
Find equivalent fractions.
HintsFor equivalent fractions they should both have the same value.
We multiply the numerator and denominator by the same number. For example,
If we were given both denominators $\frac{1}{2}$ and $\frac{?}{6}$ we would multiply by $3$ to get from $2$ to $6$.
Therefore, we multiply $1$ by $3$ also, to get the equivalent numerator.
Answer is $\frac{1}{2}$ = $\frac{3}{6}$.
Solution$\mathbf{\frac{1}{6}}$ = $\mathbf{\frac{3}{18}}$
$\mathbf{\frac{2}{7}}$ = $\mathbf{\frac{6}{21}}$
$\mathbf{\frac{4}{11}}$ = $\mathbf{\frac{28}{77}}$
$\mathbf{\frac{6}{13}}$ = $\mathbf{\frac{24}{52}}$
For example, If we were given both denominators $\frac{1}{6}$ and $\frac{?}{18}$ we would multiply by $3$ to get from $6$ to $18$.
Therefore, we multiply $1$ by $3$ also, to get the equivalent numerator.
-
Which ones are equivalent?
HintsA fraction is equivalent when you have multiplied the numerator and denominator by the same multiplier.
For example,
An example of an equivalent fraction is:
$\frac{1}{5}$ = $\frac{3}{15}$ (we have multiplied by $3$)
There are $3$ correct answers here!
SolutionCorrect answers are:
- $\mathbf{\frac{6}{9}}$ ($\frac{2}{3}$ multiplied by $3$)
- $\mathbf{\frac{14}{21}}$ ($\frac{2}{3}$ multiplied by $7$)
- $\mathbf{\frac{10}{15}}$ ($\frac{2}{3}$ multiplied by $5$)
-
Find the equivalent numbers of red apples.
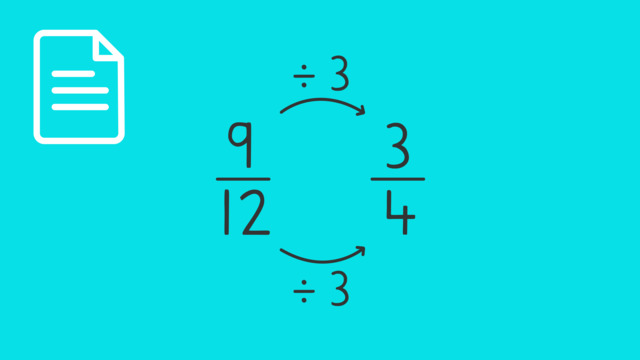
HintsThe fraction of red apples is $\frac{9}{12}$.
We are looking for equivalent fractions to this.
Equivalent is when we multiply the numerator and denominator by the same number.
Example of an equivalent fraction to $\frac{9}{12}$.
Multiply the numerator and denominator by $10$.
9$\times$10 = $90$
12$\times$10 = $120$
An equivalent fraction is $\frac{90}{120}$.
There are $2$ correct answers.
The fraction could be smaller also!
For example, $\frac{6}{8}$ can be divided by $2$
This gives $\frac{3}{4}$, which is equivalent to $\frac{9}{12}$ when multiplied by $3$.
Solution$\mathbf{\frac{45}{60}}$ and $\mathbf{\frac{6}{8}}$ are correct!
We want fractions which are equivalent to $\frac{9}{12}$.
If we multiply by $5$ we get the answer $\frac{45}{60}$.
If we divide by $3$ then multiply by $2$ we get the answer $\frac{6}{8}$.
-
What is the equivalent fraction?
HintsEquivalent fractions represent the same value.
Therefore, we multiply or divide both the numerator and denominator by the same number to make this true.
For example:
What do we need to multiply $4$ by to get to $20$?
We then multiply the numerator by this number too.
$20\div4 = 5$.
Therefore, we multiply the numerator by $5$.
$3\times5 = 15$
Solution15
We notice that the denominators are $4$ and $20$.
We multiply $4$ by $5$ to get to $20$.
Therefore, we must multiply the numerator by $5$ also.
$3 \times 5 = 15$
-
Evaluate expressions to find equivalent fractions.
HintsWhen n = $3$.
n + $1$ = $3$ + $1$ = $4$
Replace n by $3$ into each fraction to find its equivalent fraction.
When we have substituted n = $3$ into each fraction we look to find its equivalent.
For example, if we got $\frac{3}{n+5}$ we substitute n = $3$ into it.
n = $3$ and n + $5$ = $3$ + $5$ = $8$.
The equivalent fraction would be $\frac{3}{8}$
SolutionSolution is illustrated above.

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
Division with Exponents
How to Convert Decimals Expansions
Multiplication with Exponents
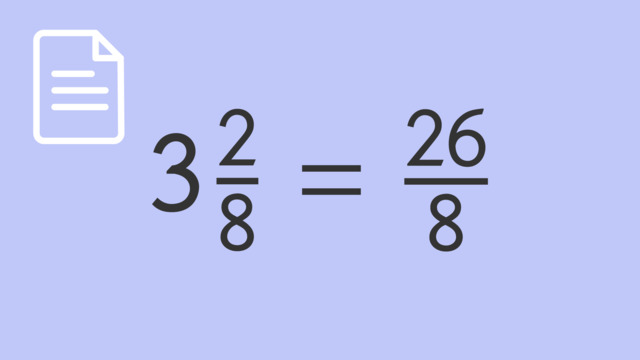
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems











