Comparing Fractions
- Comparing Fractions
- Understanding Comparing Fractions
- Comparing Fractions – Strategies
- Same Denominator Comparison
- Same Numerator Comparison
- Comparing Fractions with Different Numerators and Denominators
Learning text on the topic Comparing Fractions
Comparing Fractions
Welcome to our exploration of comparing fractions! Fractions are fundamental in mathematics and are frequently encountered in daily life, from dividing a pizza to sharing a cake. Understanding how to compare fractions is crucial in determining which fraction represents a larger or smaller part of a whole. This guide will delve into the methods and rules for comparing fractions, enhancing your mathematical skills and practical understanding.
Understanding Comparing Fractions
It is important to remember the parts of a fraction in this topic. Consider the fraction $\frac{3}{4}$: here, the numerator is 3, and the denominator is 4, meaning we have 3 parts out of a total of 4 equal parts. You can refresh your understanding of fractions by checking out What are Fractions?.
As you may already know, fractions represent parts of a whole. The process of comparing fractions involves determining which fraction is larger or smaller, or if they are equal. This skill is essential for solving real-world problems and mathematical reasoning.
To express the relationship between two fractions that are being compared, we use the symbols $>$ (greater than), $<$ (less than), and $=$ (equal to).
Comparing fractions means examining two or more fractions to decide which is larger or smaller, or if they are equal.
Before we move on, let’s check your understanding so far.
Comparing Fractions – Strategies
There are three ways you can compare fractions and these depend on whether the fractions have:
- The same denominator
- The same numerator
- Different numerator and denominator
Let’s dive into each strategy and see fraction comparison examples for each one.
Same Denominator Comparison
For fractions with the same denominator, the focus is on the numerator. In this case, the fraction with the greatest numerator is larger. This is because the same denominator means that each part is of the same size.
Let's compare $\frac{2}{5}$ and $\frac{3}{5}$. Both have the denominator 5, so we look at the numerators. Since 3 is greater than 2, this means that $\frac{2}{5}$ $<$ $\frac{3}{5}$.
Same Numerator Comparison
For fractions with identical numerators, the focus shifts to the denominators. In this case, the fraction with the smaller denominator is larger. This is because a smaller denominator means that the whole has been shared into less equal parts.
Consider comparing $\frac{1}{3}$ and $\frac{1}{5}$. Both have the numerator 1. Here, 5 (the denominator of $\frac{1}{5}$) is larger than 3 (the denominator of $\frac{1}{3}$). This means that $\frac{1}{3}$ $>$ $\frac{1}{5}$.
Comparing Fractions with Different Numerators and Denominators
Comparing fractions with different numerators and denominators requires finding a common denominator, typically the least common multiple (LCM) of the denominators.
To compare $\frac{2}{3}$ and $\frac{1}{4}$, first determine the LCM of 3 and 4, which is 12. Rewrite each fraction with the common denominator of 12: $\frac{2}{3}$ becomes $\frac{8}{12}$, and $\frac{1}{4}$ becomes $\frac{3}{12}$. Now, compare these new fractions: $\frac{8}{12}$ is greater than $\frac{3}{12}$. This means that $\frac{2}{3}$ $>$ $\frac{1}{4}$.
Below is a simplified version of the above comparison strategies for you to reference, or make a copy of!
| Situation | Comparison Method | Example | Result |
|---|---|---|---|
| Same Denominator | Compare Numerators | $\frac{2}{5}$ vs $\frac{3}{5}$ | $\frac{2}{5}$ $<$ $\frac{3}{5}$ |
| Same Numerator | Compare Denominators | $\frac{1}{3}$ vs $\frac{1}{5}$ | $\frac{1}{3}$ $>$ $\frac{1}{5}$ |
| Different Numerators and Denominators | Find Common Denominator | $\frac{2}{3}$ vs $\frac{1}{4}$ | $\frac{2}{3}$ $>$ $\frac{1}{4}$ |
Fraction Comparison Examples – Guided Practice
Let’s compare the fractions $\frac{1}{4}$ and $\frac{1}{3}$, which both have the same numerator.
Comparing Fractions – Application
Below are some problems for you to try and solve, using the different strategies that have been covered in this text.
Comparing Fractions – Summary
- Comparing fractions involves determining which fraction is larger, smaller, or if they are equal.
- When comparing fractions with the same numerator, we look at the denominator. The fraction with the smaller denominator is the greater one.
- When comparing fractions with the same denominators, we look at the numerators. The fraction with the greater numerator is the greater one.
- When comparing fractions with different numerators and denominators, we need to find equivalent fractions with the same denominators.
- To express the relationship between two fractions that are being compared, we use the symbols $>$ (greater than), $<$ (less than), and $=$ (equal to).
Continue exploring fraction comparison with our interactive problems, videos, and worksheets on our platform. If you are ready to challenge yourself, check out Comparing Fractions Using Cross Multiplication. Mastering fractions will not only boost your math skills but also enhance your problem-solving abilities in everyday life!
Comparing Fractions – Frequently Asked Questions
Comparing Fractions exercise
-
Compare the fractions with the same denominator.
HintsWhen we compare fractions with the same denominator, we need to look at the numerator.
Remember,
- < means less than
- > means greater than.
There are two correct choices.
For example, $\dfrac{2}{5}$ is less than $\dfrac{3}{5}$ because $2 < 3$.
SolutionThe two correct comparisons are:
- $\frac{1}{4}$ < $\frac{3}{4}$
- $\frac{7}{9}$ > $\frac{4}{9}$
To compare fractions with the same denominator, we look at the numerator.
Here, 1 < 4 therefore, $\frac{1}{4}$ < $\frac{3}{4}$ and 7 > 4 therefore, $\frac{7}{9}$ > $\frac{4}{9}$.
_____________________________________________________
These two choices are incorrect:
- $\frac{2}{7}$ > $\frac{5}{7}$ 2 is actually less than 5 so it should read $\frac{2}{7}$ < $\frac{5}{7}$.
- $\frac{8}{11}$ < $\frac{3}{11}$ 8 is actually greater than 3 so it should read $\frac{8}{11}$ > $\frac{3}{11}$.
-
Compare the fractions with the same numerator.
HintsRemember, for fractions with the same numerators, we need to look at the denominators. In this case, the fraction with the smaller denominator is larger. This is because a smaller denominator means that the whole has been shared into fewer equal parts.
In this example, we can see that $\frac{1}{3}$ is greater than $\frac{1}{5}$ because the whole has been shared into fewer parts so one of those parts is larger.
You could draw fraction bars to help you compare the fractions above.
Solution1.$\frac{1}{3}$ > $\frac{1}{6}$
2.$\frac{2}{7}$ < $\frac{2}{3}$
3.$\frac{5}{8}$ < $\frac{5}{6}$
4.$\frac{1}{5}$ = $\frac{1}{5}$
5.$\frac{9}{10}$ > $\frac{9}{14}$
-
How do we compare fractions with different denominators and numerators?
HintsTo compare fractions with different numerators and denominators, we make the bottom number of each fraction the same.
When converting $\frac{1}{3}$ to a fraction with a denominator of 12, we multiply the denominator of 3 by 4. We then also need the multiply the numerator by 4 too.
To compare $\frac{4}{12}$ and $\frac{9}{12}$, imagine a pie split into 12 pieces. One has 4 pieces left and one has 9 pieces left.
Which one has more pieces left?
SolutionWhen we compare fractions with different denominators and numerators, we must find a common denominator This could be the lowest common multiple or LCM.
If we were comparing $\frac{1}{3}$ and $\frac{3}{4}$, we would need to find a common denominator of 3 and 4. To do this, we can multiply 3 x 4 to get 12.
Next, rewrite each fraction with a denominator of 12.
$\frac{1}{3}$ = $\mathbf{\frac{4}{12}}$ and $\frac{3}{4}$ = $\mathbf{\frac{9}{12}}$.
Now we can compare these fractions. $\frac{4}{12}$ is less than $\frac{9}{12}$ therefore
$\frac{1}{3}$ is less than $\frac{3}{4}$.
-
Can you order the fractions?
HintsCan you find a common denominator for all of the fractions?
A common denominator for all of the fractions is 24.
Convert all of the fractions so they have 24 as a denominator and then compare.
Draw visual representations of each fraction if this helps you.
SolutionThe correct order of the fractions from smallest to greatest is:
1.$\frac{1}{12}$ = $\frac{2}{24}$
2.$\frac{1}{6}$ = $\frac{4}{24}$
3.$\frac{6}{24}$
4.$\frac{5}{12}$ = $\frac{10}{24}$
5.$\frac{1}{2}$ = $\frac{12}{24}$
6.$\frac{2}{3}$ = $\frac{16}{24}$
7.$\frac{22}{24}$
${}$
When we give all of the fractions a denominator of 24, we can compare and sort them more easily.
-
Compare the fractions.
HintsLook at the two fractions. Are the denominators or the numerators the same?
Remember, the numerator is the top number and the denominator is the bottom number.
In the fractions above, the denominators are the same so we can compare the numerators.
Use the drawings to help too, which circle has more parts shaded?
Solution$\frac{1}{5}$ < $\frac{4}{5}$
In these two fractions, the denominators are the same so we compare the numerators. 1 < 4, therefore $\frac{1}{5}$ < $\frac{4}{5}$.
We can also use the drawings and see that fewer parts are shaded in the circle representing $\frac{1}{5}$.
-
Can you compare these fractions?
HintsWhen comparing two fractions with the same denominators, compare the numerators.
If the fractions have different numerators and denominators, find a common denominator and compare.
You can also make the numerators the same and compare.
For example, we could make $\frac{1}{3}$ have a numerator of 4 by multiplying the numerator and denominator by 4 which equals $\frac{4}{12}$.
We can now see that $\frac{4}{10}$ is greater than $\frac{1}{3}$ as $\frac{4}{10}$ is greater than $\frac{4}{12}$.
Remember, for fractions with the same numerators, we need to look at the denominators. In this case, the fraction with the smaller denominator is larger. This is because a smaller denominator means that the whole has been shared into fewer equal parts.
You can draw visual representations of each fraction to help you compare.
For example, we can use these drawings to compare $\frac{1}{7}$ to $\frac{1}{4}$.
SolutionHere we can see the fractions sorted into the correct groups.

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
Division with Exponents
How to Convert Decimals Expansions
Multiplication with Exponents
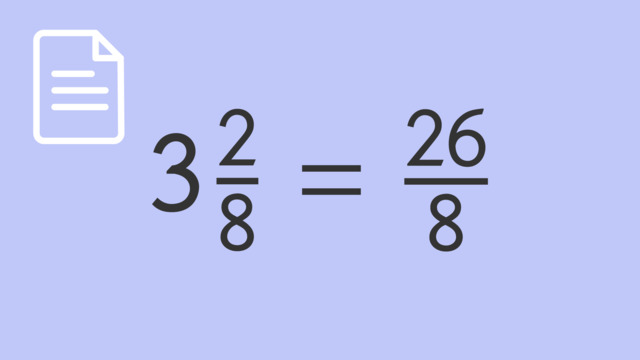
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems














