Decimal Expansions
- Decimal Expansions – Introduction
- Understanding Decimal Expansion
- How to Convert Fractions to Decimal Expansions? – Method
- Rounding and Truncating Decimal Expansions – Guided Practice
- Decimal Expansion in Real-Life Applications – Application
- Decimals Expansions – Summary
- Decimals Expansions – Frequently Asked Questions
Learning text on the topic Decimal Expansions
Decimal Expansions – Introduction
Whenever we deal with numbers in mathematics or in daily life, we often encounter figures that aren't whole numbers. These numbers may have parts or pieces that are less than one whole, and representing these parts accurately is essential for precision and clarity. This is the role of decimal expansion, a concept that is fundamental in various fields, including finance, science, engineering, and everyday commerce.
Understanding Decimal Expansion
Decimal expansion is the process of expressing numbers using a decimal point to separate the whole number part from the fractional part. It allows us to precisely represent numbers less than one, as well as numbers with fractional parts that are not whole numbers.
For instance, in the decimal expansion of 3.14, the number 3 represents the whole number part, while the digits 1 and 4 after the decimal point represent the fractional parts, specifically the tenths and hundredths respectively.
To fully grasp decimal expansions, one must become familiar with place value, such as tenths, hundredths, and thousandths, which indicate the size of the fractional part that each digit represents.
How to Convert Fractions to Decimal Expansions? – Method
To better understand how to work with decimal expansions, let's convert fractions to decimals:
Fraction to Decimal Conversion: Take the fraction $\frac{1}{2}$. To convert this to a decimal, divide the numerator (1) by the denominator (2) to get 0.5. This is the decimal expansion of $\frac{1}{2}$.
Repeating Decimals: Now, take the fraction $\frac{1}{3}$. When you divide 1 by 3, the decimal goes on forever as 0.3333..., which we represent with a repeating symbol over the 3 (0.\overline{3}).
Rounding and Truncating Decimal Expansions – Guided Practice
Rounding and truncating numbers are two techniques used to simplify decimal expansions:
Rounding: Consider the number 0.6579. To round this to the nearest hundredth, look at the third decimal place (which is 7). Since 7 is greater than 5, we round up the second decimal place to 66. So, 0.6579 rounded to the nearest hundredth is 0.66.
Truncating: To truncate the number 5.987 to the nearest tenth, simply remove the digits beyond the first decimal place without rounding. The result is 5.9.
Decimal Expansion in Real-Life Applications – Application
Decimals are not just theoretical constructs; they have practical implications in daily life:
- Money: Prices, such as $\$$3.99, are expressed in decimals.
- Measurement: Precise measurements in construction or DIY projects often require decimal representation.
- Science: Researchers use decimals for accurate data representation.
Understanding how to use decimals correctly can help you in budgeting, measuring, calculating, and analyzing data more effectively.
Decimals Expansions – Summary
Key Learnings from this Text:
- Decimal expansion allows for the precise representation of fractional parts of numbers.
- Understanding place values is crucial for interpreting and working with decimals.
- Rounding and truncating are methods used to simplify decimals.
- Decimals are widely used in real-world contexts like finance, measurement, and scientific data.
- Practicing decimal conversions and calculations can make these concepts more familiar and easier to use.
Continue to explore and practice these concepts with our interactive tools and resources designed to strengthen your numerical literacy and proficiency.
Decimals Expansions – Frequently Asked Questions
Decimal Expansions exercise
-
What is the place value of the digit $4$ in each of the numbers?
HintsPlace value charts are helpful when deciding the value of a digit.
For example, $162.57$ has $1$ hundred, $6$ tens, $2$ ones, $5$ tenths and $7$ hundredths.
There are three numbers in each group.
Solution$4$ ones
- $4.8$
- $4.93$
- $24.7$
- $0.421$
- $5.47$
- $8.4$
- $0.84$
- $8.04$
- $22.142$
-
Round each number to the given accuracy.
HintsRounding to the nearest tenth means the number is written up to the tenths place value.
We have to decide whether to round up or down each time. If the digit in the hundredths place is greater than $5$ we round up. If the digit is less than $5$ it stays the same.
For example, what is $3.86$ to the nearest tenth.
We know that it is between $3.8$ and $3.9$, which is it nearest to?
First, look at the digit in the tenths place, this is an $8$.
Next, look at the digit in the hundredths place, this is $6$.
As $6$ is greater than $5$ so we round up to get $3.9$.
Solution$2.43$ to the nearest tenth is $2.4$.
$0.238$ to the nearest hundredth is $0.24$
$2.43$ to the nearest whole number is $2$
$24.281$ to the nearest tenth is $24.3$
$0.241$ to the nearest hundredth is $0.24$
-
Convert each fraction to its decimal expansion.
HintsTo convert a fraction to a decimal we divide the numerator by the denominator.
For example, $\frac{2}{5} = 2 \div 5 = 0.4$
For numbers greater than $1$, work out the fraction first.
For example, for $3 \frac{1}{8}$.
$\frac{1}{8} = 0.125$ so $3 \frac{1}{8} = 3.125$.
Solution$\frac{1}{4} = 0.25$ because $1 \div 4 = 0.25$.
$1\frac{1}{5} =1.2$ because $1 \div 5 = 0.2$.
$\frac{3}{4} = 0.75$ because $3 \div 4 = 0.75$.
$2\frac{1}{2} = 2.5$ because $1 \div 2 = 0.5$.
-
Convert $\frac{2}{3}$ to a decimal.
HintsTo convert a fraction to a decimal, divide the numerator by the denominator.
Terminating decimals have an end point: $0.5, 3.47, 6.7032$ etc.
Recurring decimals continue forever: $0.222..., 8.4545...$ etc.
Recurring decimals are written with a dot over the repeating part: $0.\dot 2$, $8.\dot 4 \dot 5$
Our calculators will usually display a recurring decimal with the repeating digits repeated, for example, $\frac {1}{9} = 0.11111111....$.
When a question asks for the full calculator display this is how we write it. The three dots at the end indicate that it continues forever.
SolutionDivide $\bf{2}$ by $\bf{3}$.
The result is $\bf{0.66666.....}$, a decimal that goes on forever.
We represent this with a repeating symbol over the $\bf{6}$.
Written as a recurring decimal $\frac{2}{3} =$ $\bf{0.\dot 6}$
-
Determine the smallest number.
HintsWrite the numbers in a place value chart to help you.
The digits in a place value chart increase in value as we move to the left and decrease as we move to the right.
For example, comparing $5$ and $0.5$ in a place value chart, we can see that $0.5$ is less than $5$.
Solution$0.006$ is the smallest number. It has a value of $6$ thousandths.
-
Order the decimals from smallest to largest.
HintsTo start, convert the fractions to decimals.
Be careful with recurring decimals, remember the digits are repeated. So $0.\dot4$ can be written as $0.444444...$, this helps place it in the right position.
It is helpful to write all the numbers to the same number of decimal places. Use zero as placeholders to do this, so $0.2$ can be written as $0.20$.
Write all the numbers in a place value chart to help you compare them.
SolutionThe correct order is,
- $0.13$
- $0.31$
- $\frac{1}{3}$
- $1.03$
- $1\frac{3}{5}$
- $0.13$
- $0.31$
- $0.33$
- $1.03$
- $1.60$

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
Division with Exponents
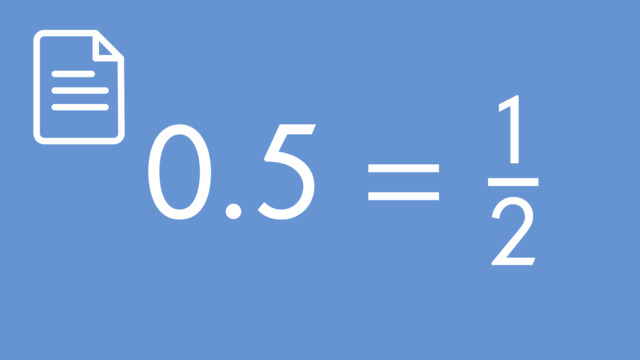
How to Convert Decimals Expansions
Multiplication with Exponents
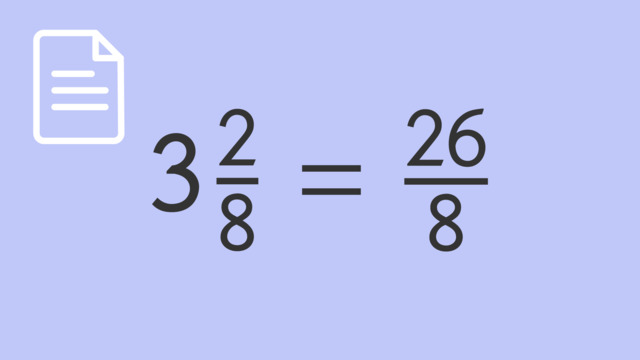
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems










