Least Common Multiples
Basics on the topic Least Common Multiples
Least Common Multiples – Introduction
Calculating the Least Common Multiple (LCM) is a fundamental skill in mathematics that can simplify many types of problems, particularly those involving fractions, ratios, or periodic events. It is the basis for finding common denominators in fractions and plays a crucial role in arithmetic and algebra.
Least Common Multiples – Definition
The Least Common Multiple of two or more numbers is the smallest positive integer that is divisible by each of the numbers without any remainder.
It's a concept that is frequently used to solve problems involving fractions, addition, subtraction, and to find equivalent fractions. Let's explore how LCM is used and why it's such an important concept in math.
Least Common Multiplies – Uses
Using the LCM allows us to find the smallest shared multiple between numbers, which facilitates operations such as adding and comparing fractions. It's also used when we want to synchronize events that happen in cycles, like traffic lights or scheduling.
How to Find Least Common Multiples – Example
The process of finding the LCM can be done in several ways, including listing the multiples, using prime factorization, or employing the greatest common divisor (GCD). Here's an example using the listing method:
Least Common Multiples – Application
LCMs have various real-world applications. They are particularly useful in situations where different cycles need to be synchronized, such as in scheduling, baking, or planning events.
Least Common Multiples – Summary
Key Learnings from this Text:
- LCM is the smallest number into which two or more given numbers can evenly divide.
- It is crucial for adding, subtracting, and comparing fractions with different denominators.
- Understanding LCMs can simplify various real-world problems and facilitate synchronization.
- While calculating LCMs, one can use the listing method, prime factorization, or the GCD approach.
Consider exploring more about LCMs and their applications in other areas of mathematics such as finding equivalent fractions and Solving Problems with Equivalent Ratios.
Least Common Multiples – Frequently Asked Questions

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
Division with Exponents
How to Convert Decimals Expansions
Multiplication with Exponents
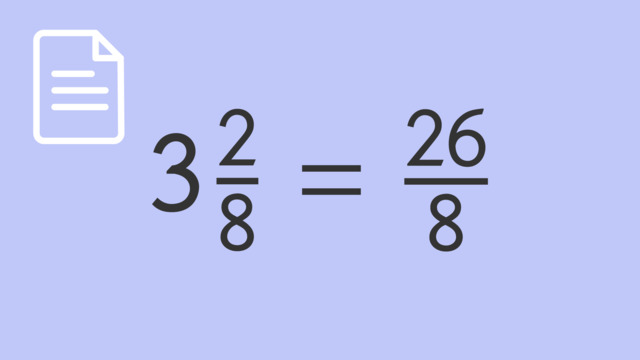
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems










