Improper Fractions and Mixed Numbers
- What are Improper Fractions?
- What are Mixed Numbers?
- Converting Mixed Numbers to Improper Fractions – Method
- Converting Improper Fractions to Mixed Numbers – Method
- Adding and Subtracting Mixed Numbers
- Multiplying and Dividing Mixed Numbers
- Simplifying Fractions
Learning text on the topic Improper Fractions and Mixed Numbers
This text is all about improper fractions and mixed numbers, key concepts in Math that you'll find incredibly useful as you move through Middle School. Additionally, understanding these will help you tackle everyday problems more efficiently—like splitting that pizza with your friends or baking cookies using a recipe. Let's get started!
What are Improper Fractions?
An improper fraction is a type of fraction where the numerator (the top number) is equal to or larger than the denominator (the bottom number). This means you have a fraction that is equal to or greater than 1.
An improper fraction looks like $\frac{5}{3}$ or $\frac{5}{5}$ where the top number is equal to or bigger than the bottom number. It represents more than one whole.
Imagine having two pizzas that have been cut into 4 slices each, and you have 5 of those slices. This situation is perfect for using an improper fraction to describe what you have.
What are Mixed Numbers?
A mixed number is a way of expressing a number that's made up of a whole part and a fractional part. It's like having some whole apples and some parts of an apple.
A mixed number is written with a whole number alongside a fraction, such as $2 \frac{1}{2}$, which means 2 whole items plus half of another one.
Understanding the concept of Fractions Greater than 1 on a Number Line is extremely helpful when trying to visualise mixed numbers and improper fractions.
Converting Mixed Numbers to Improper Fractions – Method
When it comes to working with fractions in math problems, it's often easier to deal with them when they're all written in the same form. This is why we learn how to convert a mixed number to an improper fraction.
Here's the step-by-step method for $3 \frac{2}{8}$:
| Step | What to do? | Example |
|---|---|---|
| 1. | Multiply the whole number by the denominator of the fraction. | 3 × 8 = 24 |
| 2. | Add the numerator to the product from step 1. | 24 + 2 = 26 |
| 3. | Write the result over the original denominator. | $ \frac{26}{8} $ |
You can also combine these steps into one continuous expression to convert numbers from mixed numbers to improper fractions. The example from the table can also be presented this way:
Converting Improper Fractions to Mixed Numbers – Method
Sometimes it's more intuitive to work with improper fractions when they are in the form of mixed numbers, especially when you're dealing with amounts or measurements. This is why learning to convert an improper fraction to a mixed number is a valuable skill.
Here's the step-by-step method for $\frac{13}{6}$:
| Step | What to do? | Example |
|---|---|---|
| 1. | Divide the numerator by the denominator to find the whole number part of the mixed number. | 13 ÷6 = 2 remainder 1 |
| 2. | The remainder becomes the new numerator of the fractional part. | remainder 1 |
| 3. | Write the whole number alongside the new fraction with the original denominator. | $2 \frac{1}{6}$ |
Adding and Subtracting Mixed Numbers
When you add or subtract mixed numbers, treat the whole numbers and the fractions separately, ensuring that the fractions have the same denominator.
For example, adding $1 \frac{3}{8}$ and $2 \frac{2}{8}$ together, we combine the whole numbers (1 + 2) and the fractions ($ \frac{3}{8} + \frac{2}{8}$) to get $3 \frac{5}{8}$.
Multiplying and Dividing Mixed Numbers
For multiplication and division of mixed numbers, it's best to convert them to improper fractions first. Multiply or divide as usual, and if dividing, remember to use the reciprocal of the divisor.
Simplifying Fractions
After any operation with mixed numbers or improper fractions, it's important to simplify your answer. This means expressing the fraction in its simplest form by reducing it to the lowest terms.
You may consider converting a mixed number to an improper fraction as it makes solving the problem easier or helps in understanding the result better. However, this conversion is not always necessary and depends on the context or preference in representation.
Improper Fractions and Mixed Numbers – Summary
Key Learnings from this Text:
- A mixed number combines a whole number with a fraction.
- Converting between mixed numbers and improper fractions allows for easier calculations.
- To convert Mixed Numbers to Improper Fractions, you need to multiply the whole number by the denominator and add the numerator. This becomes your new numerator, keep the denominator the same.
- Fraction operations with mixed numbers involve ensuring the same denominator for addition/subtraction and converting to improper fractions for multiplication/division.
- Simplifying fractions makes mixed numbers easier to understand and work with.
Ready to test your skills further? Check out other fun math challenges and resources available on our website!
Improper Fractions and Mixed Numbers – Frequently Asked Questions
Improper Fractions and Mixed Numbers exercise
-
What does each keyword mean?
HintsA fraction is made up of a numerator and denominator. Which way round do they go?
Proper fractions are those with a quantity less than one whole. Improper fractions have a quantity equal to or greater than one whole.
SolutionNumerator - The top number in a fraction.
Denominator - The bottom number in a fraction.
Improper Fraction - When the numerator is equal to or larger than the denominator.
Proper Fraction - When the numerator is smaller than the denominator.
Mixed Number - A number made up of a whole part and a fractional part. -
What is represented by the diagram?
HintsThe denominator is the number of equal parts per cake.
The numerator is the number of pieces of cake highlighted.
There are two possible answers, an improper fraction and a mixed number.
SolutionEach cake has 8 equal parts, this tells us that the denominator is 8.
There are 9 pieces of cake highlighted, this tells us the numerator is 9.
The correct answers are $\mathbf{\frac{9}{8}}$ and $\mathbf{1 \frac{1}{8}}$. -
What are the equivalent mixed numbers and improper fractions?
HintsTo convert a mixed number to an improper fraction, multiply the whole number by the denominator then add the numerator. Write this number over the original denominator.
To convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient is the whole number part of the mixed number and the remainder becomes the new numerator over the original denominator.
For example: $\frac{5}{3}$ = $1 \frac{2}{3}$
Solution$\mathbf{2 \frac{3}{4}}$ = $\mathbf{\frac{11}{4}}$ because 2 x 4 + 3 = 8 + 3 = 11 giving $\frac{11}{4}$
$\mathbf{3 \frac{1}{2}}$ = $\mathbf{\frac{7}{2}}$ because 3 x 2 + 1 = 6 + 1 = 7 giving $\frac{7}{2}$
$\mathbf{\frac{7}{4}}$ = $\mathbf{1 \frac{3}{4}}$ because 7 $\div$ 4 = 1 remainder 3 giving $1 \frac{3}{4}$
$\mathbf{\frac{18}{5}}$ = $\mathbf{3 \frac{3}{5}}$ because 18 $\div$ 5 = 3 remainder 3 giving $3 \frac{3}{5}$ -
Adding and subtracting fractions.
HintsYou can add the whole numbers and the fractions separately then put them together to form the answer.
You can convert the mixed numbers to improper fractions before adding or subtracting, then convert the answer back to a mixed number.
If you subtract using the mixed numbers watch out for negative fractions. You must subtract the fractional part from the whole number. If you want to avoid negative fractions you should convert the mixed numbers to improper fractions first.
- For example, using a negative fraction,
- Or, changing to improper fractions,
Solution$\mathbf{{2 \frac{2}{9}}} + \mathbf{{3 \frac{5}{9}}} = \mathbf{{5 \frac{7}{9}}}$
because $2 + 3 = 5$ and ${\frac{2}{9}} + {\frac{5}{9}} = {\frac{7}{9}}$
$\mathbf{{6 \frac{3}{5}}} - \mathbf{{2 \frac{2}{5}}} = \mathbf{{\frac{21}{5}}}$
because ${6 \frac{3}{5}} = {\frac{33}{5}}$ and ${2 \frac{2}{5}} = {\frac{12}{5}}$ then ${\frac{33}{5}} - {\frac{12}{5}} = {\frac{21}{5}}$
$\mathbf{{5 \frac{1}{7}}} - \mathbf{{3 \frac{5}{7}}} = \mathbf{{1 \frac{3}{7}}}$
because $5 - 3 = 2$ and ${\frac{1}{7}} - {\frac{5}{7}} = { \frac{-4}{7}}$ then $2 - {\frac{4}{7}} = {1 \frac{3}{7}}$ -
Can you identify the fraction type?
HintsIn a proper fraction the numerator is smaller than the denominator.
In an improper fraction the numerator is equal to or more than the numerator.
A mixed number has a whole part and a fractional part.
There are three items to be assigned to each group.
SolutionProper Fractions - $\mathbf{\frac{3}{4}}$, $\mathbf{\frac{1}{4}}$, $\mathbf{\frac{3}{8}}$
Improper Fractions - $\mathbf{\frac{4}{3}}$, $\mathbf{\frac{8}{5}}$, $\mathbf{\frac{10}{5}}$
Mixed Numbers - $\mathbf{2 \frac{1}{2}}$, $\mathbf{3 \frac{3}{4}}$, $\mathbf{1 \frac{1}{5}}$ -
What is $2\frac{3}{10}$ $\times$ $3$?
HintsWhen multiplying mixed numbers remember to convert them to improper fractions first.
When multiplying a fraction by a whole number we only multiply the numerator by the whole number i.e. $\frac{5}{4} \times 2 = \frac{10}{4}$
Solution$2\frac{3}{10} \times 3 = \frac{23}{10} \times 3 = \frac{69}{10} = 6\frac{9}{10}$

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
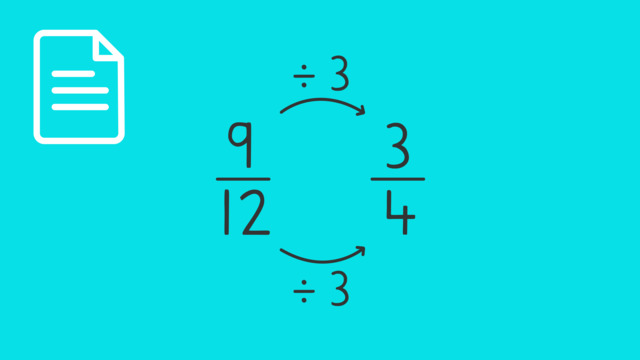
Simplifying Fractions

Temperature Conversion

Decimal Expansions
Division with Exponents
How to Convert Decimals Expansions
Multiplication with Exponents
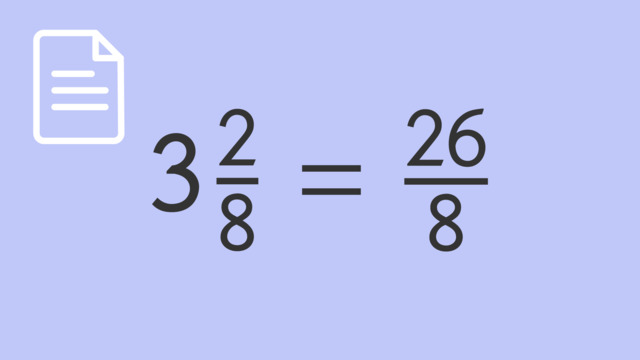
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems
















