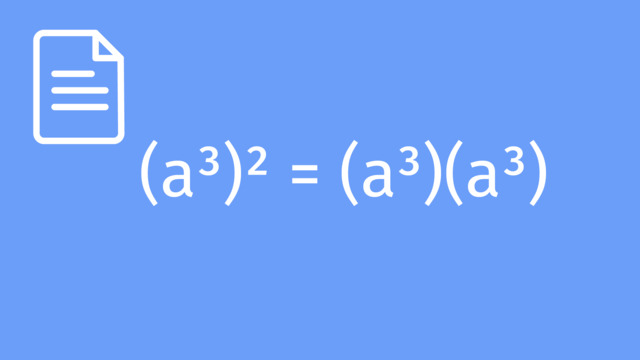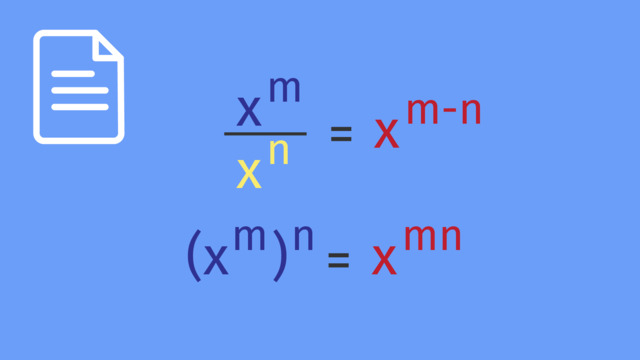Exponential Notation


Basics on the topic Exponential Notation
After this lesson you will be able to use exponents, and determine whether a number raised to a given power will be positive or negative.
The lesson begins with the definition of exponential notation. This leads to an explanation of why negative numbers raised to an even power produce positive results, while negative numbers raised to an odd power produce negative results.
Learn about exponents by helping Wade and Skeeter decide what to do with the magical fish!
This video includes key concepts, notation, and vocabulary such as: base (the number being multiplied); exponent (the number of times the base is being multiplied by itself); the phrase, “x raised to the nth power” (where n is the exponent and x is the base); square (x raised to the second power is called the “square” of x); and cube (x raised to the third power is called the “cube” of x).
Before watching this video, you should already be familiar with exponential notation using base 10, and multiplication as repeated addition.
After watching this video, you will be prepared to learn about fractional or negative exponents.
Common Core Standard(s) in focus: 8.EE.A.1 A video intended for math students in the 8th grade Recommended for students who are 13-14 years old
Transcript Exponential Notation
Wade and Skeeter have pulled up an unusual fish in their nets. "Skeeter thinks they should sell it at the market and pay their debts, but Wade isn't so sure. " I mean, not only is this fish talking but he claims that if Wade and Skeeter will set him free he can transform their debt into a fortune, just by using exponential notation. Exponential notation is the shortcut we use for expressing repeated multiplication. So we can express 3 times 3 times 3 times 3 as "3 to the 4th power". 3 is the base - it's the number which is repeatedly multiplied. 4 is the exponent - it's the number of 3's that were multiplied. In general, given any number 'x', multiplied 'n' times, we can write the result as 'x' to the nth power". This applies to any rational number, including fractions and negative numbers. One-half, multiplied by itself 6 times can be written as one-half to the sixth power. Negative 5, multiplied by itself 6 times, can be written as negative 5 to the sixth power. Notice that we enclose fractions and negative numbers in parentheses to show that the entire number is raised to the given power. This is especially important when entering exponents into your calculator. Let's check back in with Wade and Skeeter. They started the day 5 dollars in debt. That means they have negative 5 dollars. The talking fish gives them three magical options to choose from. Let's see if we can use exponential notation to evaluate them. The first option is to multiply their money times three-fifths, every day for 6 days. We can write that as negative 5 times three-fifths multiplied by itself 6 times. How would you re-write that using exponential notation? Well, three-fifths is our base, since that is the number we are multiplying over and over. Which makes 6 our exponent, since that's the number of times we're multiplying. And we multiply all of that by negative 5. Ok, on to the second magical option, in which the fish offers to multiply their money times itself for 9 days. In this option, what number should we use for our base? We're multiplying negative 5 times itself, so that is our base. Which makes 9 our exponent. The third and final option the fish offers is to multiply their money times itself for 8 days. So we can write that as negative 5 to the eighth power. Now that we have all options in exponential notation, let's help Skeeter and Wade decide which choice will make them rich! Considering the first option, do you think that negative five times three-fifths to the sixth power will be positive or negative? Well, we have a negative number times a positive number so we can expect a negative result. Using a calculator, we find that negative 5 times three-fifths to the sixth is about negative 23 cents. How about the next two options, which involve a negative base raised to a power? To understand how negative bases interact with exponents, let's look at another example. Consider negative 5, squared. That's negative 5 times negative 5, or positive 25. If we multiply negative 5 times itself one more time that's 25 times negative 5, or negative 125. If we multiplied that again by negative 5 it would give us a positive result. One more time would give us a negative result. Are you starting to see the pattern? A negative base raised to an even power always gives us a positive result. While a negative base raised to an odd power gives us a negative result. So with that in mind, which amount of money would you rather have: negative 5 dollars raised to the ninth power or negative 5 dollars to the eight? Negative 5 to the ninth is a negative base raised to an odd power, so the result will be negative. Negative 1,953,125 dollars, to be exact. How about negative 5 to the eighth? That's a negative base raised to an even power, so the result will be positive. From negative 5 dollars to positive 390,625 dollars? Now that's what I'm talking about! Option 3 turns Skeeter and Wade's debt into profit! To review, exponential notation is the shortcut for writing repeated multiplication of a number by itself. The number multiplied is the base and the number of times we multiply is the exponent. When working with fractional or negative bases remember to use parentheses to avoid confusion. And finally, just in case you run into a talking fish remember that a negative base raised to an odd power gives a negative result while an even power gives us a positive result. Skeeter and Wade have made their choice to cash in and set the fish free. And right on cue, he grants them their reward! Filthy stinkin' rich? More like, like filthy sinking rich! Ha! Well, you know what they say: when working with exponents, be careful what you fish for!
Exponential Notation exercise
-
Identify the key aspects of exponential notation.
HintsExponential Notation is a shortcut used to express repeated multiplication.
$5^2 = 5\cdot5$
$5^3 = 5\cdot5\cdot5$
$5^4 = 5\cdot5\cdot5\cdot5$
$3^5$ is written in exponential notation.
We can read this as "three to the fifth power".
To evaluate this expression, we can multiply 3 by itself, five times.
$3\cdot3\cdot3\cdot3\cdot3 = 243$
SolutionThis expression is written in exponential notation.
It is read as "six to the fourth power".
The $6$ is the base and the $4$ is the exponent.
The expression expanded would be $\mathbf{6\cdot6\cdot6\cdot6}$.
The solution is $\mathbf{1,296}$.
-
Expanding expressions written in exponential notation.
HintsRemember, when the negative sign is inside the parentheses, the number is negative and is repeatedly multiplied.
$(-n)^3=(-n)(-n)(-n)$
If the negative sign is outside the parentheses, the number is positive which is being repeatedly multiplied, and the negative sign is applied at the end.
$-(w)^3=-(w)(w)(w)$
SolutionThe solution is $\mathbf{(-7)(-7)(-7)(-7)}$.
Since the negative sign is inside the parentheses with the 7, it is a negative 7 that will multiplied by itself four times.
-
Identify each expression in exponential notation.
HintsPay attention to the differences between the two numbers used for exponential notation. The larger number is the base, and the smaller number is the exponent.
For example: $5^3$
The $5$ is the base, and the $3$ is the exponent.
The base is multiplied by itself the amount of times the exponent says.
$(-x)^5=(-x)(-x)(-x)(-x)(-x)$
Solution$(-3)^4=(-3)(-3)(-3)(-3)$
$4^3 = (4)(4)(4)$
$3^4 = (3)(3)(3)(3)$
$3^3=3\cdot3\cdot3$
$(-4)^4=(-4)(-4)(-4)(-4)$
-
Identify the sign of each expression in exponential notation.
HintsWhen the base is negative, it is important to pay attention to the exponent to see if it is even or odd.
Even Exponent = Positive Result
Odd Exponent = Negative Result
The base can be any negative value for this rule to apply.
For example:
$(-m)^\mathbf{2}$ The exponent of $2$ is even, so this equals a positive answer.
$(-m)^\mathbf{3}$ The exponent of $3$ is odd, so this equals a negative answer.
Solution$(-h)^{2}$ = positive
$(-3)^{18}$ = positive
$(-4)^{6}$ = positive
$(-5)^{8}$ = positive
$(-m)^{10}$ = positive
$(-1)^{3}$ = negative
$(-e)^{1}$ = negative
$(-9)^{7}$ = negative
$(-2)^{15}$ = negative
$(-w)^{11}$ = negative
-
Rewrite the expression using exponential notation.
HintsHere, the $3$ is the base and the $4$ is the exponent. As you can see, the $3$ will be multiplied by itself $4$ times in order to find the solution.
This can be true for any number written in exponential notation.
The base is the number we multiply by itself. And the exponent tells us how many times.
For the expression $2\cdot2\cdot2\cdot2$, the $2$ is the base, since that is the number that is being multiplied repeatedly.
SolutionThe base is 2 and the exponent is 4.
$2^4$
-
Interpret values in exponential notation.
HintsRemember, the location of the negative sign can change the solution to an expression in exponential notation. If you are unsure whether the final solution will be a positive or negative value, you can always follow these steps:
- Expand the expression to show repeated multiplication.
- Follow the order of operations to find the solution.
Don't forget the rules for multiplying integers!
When the signs are the same, the product is positive.
When the signs are different, the product is negative.
Two examples that may help you find the solution easier!
$(-3)(-3)$
This has two negative numbers, so our product must be a positive nine ($9$).
$(-3)(3)$
One number is negative, and the other is positive, so the product must be a negative nine ($-9$).
See if this can help you with a better understanding of which expressions equal 9 and which equal $-9$.
SolutionThe following expressions are equal to $9$:
$(3^2)$
$(-3)^2$
$3^2$
$(-3)(-3)$
$9^2$
$(3)(3)$
The following expressions are equal to $-9$.
$-9^1$
$-(3)^2$
$(-9)^1$
$-(3^2)$
$-(3)(3)$
$-3^2$