Adding and Subtracting Rational Numbers on a Number Line
- Adding and Subtracting Rational Numbers
- Adding and Subtracting Rational Numbers on a Number Line
- Practice Adding and Subtracting Rational Numbers Using a Number Line
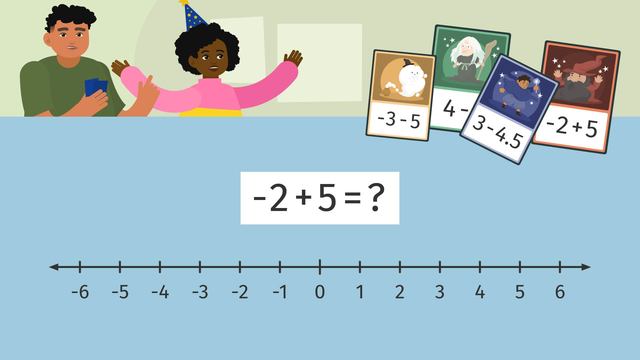

Basics on the topic Adding and Subtracting Rational Numbers on a Number Line
Adding and Subtracting Rational Numbers
In our everyday lives, we often encounter situations where we need to add or subtract different types of numbers, like fractions, decimals, and integers. These types of numbers are known as rational numbers.
Rational numbers include all integers, fractions, and decimals that can be expressed as a fraction of two integers, where the denominator is not zero. Adding and subtracting rational numbers involves combining or removing parts of these numbers while following specific rules.
Adding and Subtracting Rational Numbers on a Number Line
A number line is a helpful visual tool for understanding addition and subtraction, especially with rational numbers. It illustrates how moving up and down represents adding or subtracting rational numbers on the number line.
- Adding on a Number Line: When adding, you move to the right if the number is positive and to the left if it's negative. For example, starting at -3 and adding 4 means moving 4 steps to the right.
- Subtracting on a Number Line: Subtracting involves moving in the opposite direction. If you're subtracting a positive number, you move to the left. For example, starting at 4 and subtracting 9 means moving 9 steps to the left.
- Adding a positive to a negative number, like $-3 + 4$, moving right from $-3$ to $1$.
- Subtracting a larger number from a smaller one, like $4 - 9$, moving left from $4$ to $-5$.
Practice Adding and Subtracting Rational Numbers Using a Number Line
Use a number line to practice adding and subtracting rational numbers.
Adding and Subtracting Rational Numbers – Rules
Grasping the rules for adding and subtracting rational numbers is more practical and efficient than relying solely on visual methods like number lines. This knowledge not only streamlines calculations but also lays a foundational understanding for tackling advanced mathematical concepts in the future.
| Operation | Rule Description | Example |
|---|---|---|
| Adding with Same Sign | Add absolute values and keep the sign. | $-4 + (-2)$ = $-6$ |
| Adding with Different Signs | Subtract absolute values and keep the sign of the larger value. | $-3 + 5$ = $2$ |
| Subtracting (Convert to Addition) | Change subtraction to adding the opposite. | $7 - 9$ = $7 + (-9)$ = $-2$ |
Adding Rational Numbers with the Same Signs
To add rational numbers with the same sign - add their absolute values and keep the common sign. Adding integers is not much different than what you have learned in the past, just be sure to watch the signs!
Example: $-5 + (-3)$
- Add their absolute values: $5 + 3 = 8$.
- Keep the common negative sign: $-8$.
Adding Rational Numbers with Different Signs
To add rational numbers with different signs - subtract their absolute values and keep the sign of the number with the larger absolute value.
Example: $-5 + 3$
- Subtract their absolute values: $5 - 3 = 2$.
- Keep the sign of the number with the larger absolute value (which is -5): $-2$.
An introduction to absolute value will be useful for successfully adding integers with different signs.
Subtracting Rational Numbers
To subtract rational numbers, convert to addition, and add the opposite. For instance, $a - b$ becomes $a + (-b)$. Subtracting integers can be made much easier by following this rule!
Example: $4 - 6$
- Convert to addition: $4 + (-6)$.
- Find the sum: $-2$.
It is important to have a good understanding of integers and their opposites to become more proficient with subtracting integers!
Adding and Subtracting Rational Numbers – Exercises
Using the strategies learned, practice adding and subtracting rational numbers.
Adding and Subtracting Rational Numbers – Summary
Key Learnings from this Text:
- Rational numbers include integers, fractions, and decimals.
- When adding, if signs are the same, add the values and keep the sign. If the signs are different, subtract the values and take the sign of the larger value.
- When subtracting, add the opposite of the second number.
- A number line helps visualize these operations, especially when dealing with negative numbers.
- Understanding these concepts is crucial for practical applications like budgeting or measuring.
Adding and Subtracting Rational Numbers – Frequently Asked Questions
Transcript Adding and Subtracting Rational Numbers on a Number Line
"Okay Math Wizards, let's get ready to start the game!" Today June's after-school club will be playing a game to master their skills with 'Adding and Subtracting Rational Numbers on a Number Line'. "Here's a quick rundown of the game rules!" Remember, rational numbers are numbers that can be written as a fraction, but the denominator can not be equal to zero. A vertical or horizontal number line may be used for the game. Don't forget, zero is in the middle the positive numbers are on the right or above the zero, and the negative numbers are on the left or below the zero. When you are given an expression, the first number is where you begin. The operation in the middle tells us which direction to move, which would be up or right if positive, and down or left if negative. And the second number is the number of times you move on the number line. June's friend, Luis will start the game. Negative two plus five. On our number line, we will start at negative two. The addition sign tells us we will move right five units negative one, zero, one, two, three. Where you land is your answer, so, three! Now, it's June's turn to play. The next card is four minus seven. Starting on the positive four, we will move seven units to the left to subtract. This will result in negative three. Luis will take his next turn and will use a vertical number line. The card says three minus four and one-half. Starting with positive three, Luis will subtract, or move down four and one-half units. Where will he land? Luis lands on negative one and a half. It's June's turn, again and her next card is negative three, minus five. Starting at negative three, we must move down five units further into the negative zone. This will give us a solution of negative eight. "Hey, Luis what about one more round you know, just for some extra practice!" Let's see if you can help Luis and June find their final scores. Pause the video here, and use the number line to find out what their final scores will be! For Luis, starting at negative one and a half, move right two and a half units. Luis will end with one single point. June starts all the way down at negative eight and moves four units to the right. She will end at negative four and is definitely not very happy about that. It looks like the final score is Luis... "Freeze! I've been waiting for this chance!" "I would like to use my Sorcerer's Secret bonus card before my turn is officially over." In case you haven't played this game before, this special card will take the absolute value of all player's final scores when used in the last round. The card does not change Luis' score, but, June's negative four is now a positive four! "I win!"
Adding and Subtracting Rational Numbers on a Number Line exercise
-
Identify the addition expression represented by the number line.
HintsUsing a number line can help you solve an addition or subtraction problem with rational numbers.
- The first number is where you start.
- The sign determines the direction you move.
- The second value is how many times you move.
The $-3$ is where you start, so the expression must also start with a $-3$.
The jumps are moving in the right direction which is towards positive. This means that addition is the operation.
There are a total of $5$ jumps, so we are adding $\bf{5}$.
SolutionThe expression $\bf{-3 + 5}$ represents the number line.
The arrow starts at $-3$ and jumps $5$ to the right for addition.
The solution is $2$.
-
Understand how to use a number line to add and subtract rational numbers.
HintsUsing a number line can help you solve an addition or subtraction problem with rational numbers.
- The first number is where you start.
- The sign determines the direction you move.
- The second value is how many times you move.
Notice that the number line starts at $-4$ because that is the first number.
The arrow then moves $3$ units to the right for addition.
The solution is $-1$.
Remember, the operation determines the direction you move on the number line.
For addition ($+$), you move to the right.
For subtraction ($-$), you move to the left.
SolutionHere you can see the number lines to represent each expression.
- $0-4=-4$
- $-4+4=0$
- $-4+5=1$
- $4-5=-1$
-
Add and subtract rational numbers using a number line.
HintsIt may help you to create a number line on paper to find the solutions.
Remember, the right side of the number line is positive numbers, and the left side is negative numbers.
Half values are found directly between the integers. For example, $-1.5$ is between $-2$ and $-1$.
The same rule applies as with whole numbers, the operation determines the direction, and the second value determines how far you go!
SolutionSolutions:
- $5 - 7 = \bf{-2}$
- $-1.5 + 3.5 = \bf{2}$
- $3.5 - 5 = \bf{-1.5}$
- $-2.5 - 0.5 = \bf{-3}$ (displayed above on the number line)
-
Use a number line to add and subtract rational numbers.
HintsUsing a number line can help you solve an addition or subtraction problem with rational numbers.
- The first number is where you start.
- The sign determines the direction you move.
- The second value is how many times you move.
The left side has negative numbers.
The right side has positive numbers.
Be sure to pay careful attention to the signs of the first number. Starting in the wrong spot will result in landing on the wrong solution!
SolutionExpressions that have a solution of $-1$
- $-4 + 3$
- $6 - 7$
- $-1 + 0$
- $-2 + 1$
- $-4 + 5$
- $6 - 5$
- $-1 + 2$
- $-3 + 4$
-
Use a number line to add and subtract rational numbers.
HintsWhat is the first number in the math problem?
This number is where you start on the number line.
Starting at $2$, next use the operation to figure out which direction you will move on the number line.
Addition: Move right on a horizontal number line.
Subtraction: Move left on a horizontal number line.
The operation in $2 - 6$ is subtraction, so move left $6$ units to find the solution.
$2 - 6 =$ ?
Solution$\bf{2 - 6 = -4}$
- Start at $2$.
- Move $6$ units to the left for subtraction.
- End at $-4$.
-
Use your understanding of operations of rational numbers on a number line to solve a problem.
HintsStart by writing a math sentence to represent the situation.
- How much did June start with?
- What happened next, did her money increase or decrease?
- By how much?
- Etc...
Once you have a math sentence, a number line can be used to help determine her final amount of money.
Draw one on paper to help you solve this problem!
SolutionJune now has $\bf{\$4.50}$.
The math sentence we can use to solve is $3 - 4.5 + 6$.

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
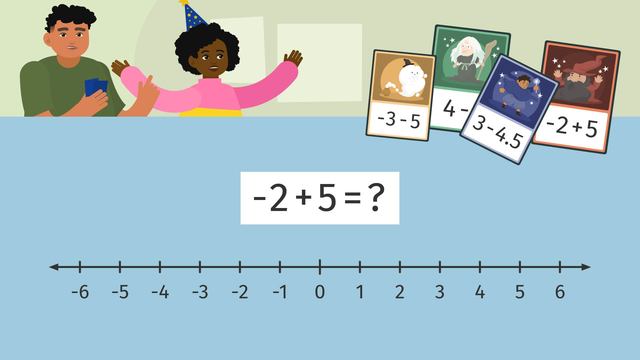
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
Division with Exponents
How to Convert Decimals Expansions
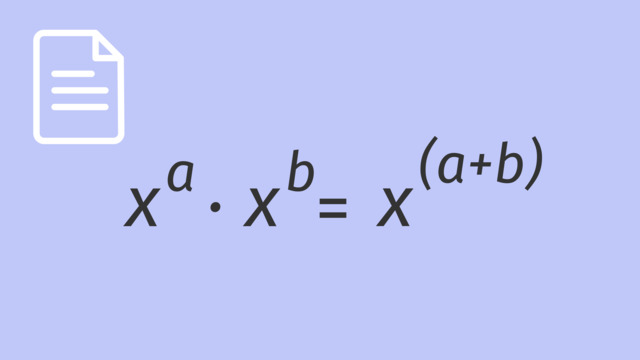
Multiplication with Exponents
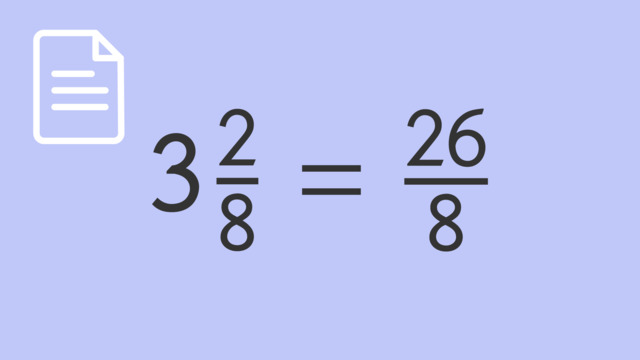
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems













