Multiplication with Exponents
- Introduction to Multiplying Exponents
- Multiplying Exponents – Rules
- Multiplying Exponents – Same Base
- Multiplying Exponents – Different Base
- Multiplying Exponents – Different Base, Same Exponent
- Multiplying Exponents – Power of a Power
Learning text on the topic Multiplication with Exponents
Introduction to Multiplying Exponents
Exponents are more than just numbers on paper; they're a key part of the math you'll encounter in and out of school. Think of exponents as a shortcut for repeated multiplication, simplifying how we handle larger numbers. In everyday life, you see them in situations like calculating how fast a popular video goes viral or understanding how interest on your savings account works. Let's explore multiplying powers with the same base! We'll uncover the logic behind the keep the base, add the exponents rule through easy expansions, making this concept simple to grasp.
Multiplying Exponents – Rules
Multiplying exponents is a fundamental aspect of algebra that follows specific rules, making complex calculations more manageable. Whether dealing with the same base, different bases, powers of a power, or working within parentheses, each scenario has its own set of guidelines. Let's explore these varied rules to understand how to effectively multiply exponents in different mathematical contexts.
Multiplying Exponents – Same Base
To grasp why we add exponents when multiplying powers of the same base, it's helpful to look at the process of expansion.
When multiplying powers with the same base, keep the base the same and find the sum of the exponents.
Let's use concrete numbers for clarity. Consider $2^3 \cdot 2^2$. Here, $2$ is the base, and $3$ and $2$ are the exponents. We can expand these terms to understand the addition of exponents:
- $2^3$ means multiplying $2$ by itself $3$ times, which is $2 \cdot 2 \cdot 2$.
- $2^2$ means multiplying $2$ by itself $2$ times, which is $2 \cdot 2$.
When you multiply $2^3$ and $2^2$, you're essentially multiplying $2$ by itself $3 + 2=5$ times. Therefore, $2^3 \cdot 2^2 = 2^{(3+2)} = 2^5$.
Multiplying Exponents – Different Base
When dealing with expressions that have different bases and exponents, such as $a^x$ and $b^y$, it's essential to treat each base and its exponent separately. Here, $a$ and $b$ represent different bases, while $x$ and $y$ are their respective exponents.
For different bases, calculate each exponential term individually. The multiplication of $a^x$ and $b^y$ can be expressed as $a^x \times b^y = (a^x) \times (b^y)$. Each base is raised to its exponent, and the results are then multiplied.
In practice, this means you should first evaluate $a^x$ and $b^y$ separately and then multiply these outcomes to find the final result.
Multiplying Exponents – Different Base, Same Exponent
When multiplying exponents that have different bases but the same exponent, the process is slightly different from other scenarios in exponent multiplication. This situation often arises in various mathematical contexts and requires a distinct approach.
When multiplying powers with different bases but the same exponent, you multiply the bases first and then apply the common exponent to the result.
To understand this, consider an example like $2^3 \cdot 3^3$. Here, $2$ and $3$ are different bases, but both have the same exponent, $3$. The multiplication can be approached by first multiplying the bases and then applying the exponent:
- First, multiply the bases: $2 \times 3 = 6$.
- Then, apply the common exponent: $6^3$.
So, $2^3 \cdot 3^3 = 6^3$.
Multiplying Exponents – Power of a Power
In multiplying exponents, another important concept is the Power of a Power rule. This rule comes into play when you have an exponent raised to another exponent, like $(n^a)^b$.
The Power of a Power rule states that when you raise a power to another power, you multiply the exponents. This is written as $(n^{a})^b = n^{a \cdot b}$.
For example, $(3^2)^4$can be expanded as $3^{2 \cdot 4} = 3^8$. This shows that you multiply the exponent outside the parenthesis with the exponent inside.
Understanding the Power of a Power law is crucial as it simplifies complex expressions and is a key component in algebra and higher-level math. For further information about this rule, this video will provide you with a chance to learn more: Numbers in Exponential Form Raised to a Power.
If you are finding it hard to follow the text, we recommend consolidating your understanding of Exponential Notation by watching this video: Exponential Notation
Multiplying Exponents – Examples
See how much you understand about multiplying exponents so far with this interactive quiz!
The process of multiplying exponents can be used in some real-world problems, such as Multiplying and Dividing Numbers in Scientific Notation which is helpful when working with very large or very small numbers.
Multiplying Exponents – Practice
Tips for Multiplying Exponents
- Understand the Base: Remember that the base number remains the same when multiplying exponents.
- Expand for Clarity: Breaking down the expression by expanding each term can help visualize why the exponents are added.
- Add the Exponents: Focus on adding the exponents when the base is the same. This is key to simplifying the expression correctly.
- Check Your Work: After simplifying, it's always good practice to check your work by expanding the expression to ensure it matches the original values.
| Multiply | Expansion | Add the Exponents | Simplify |
|---|---|---|---|
| $6^3 \cdot 6^5$ | $(6 \cdot 6 \cdot 6) \cdot (6 \cdot 6 \cdot 6 \cdot 6 \cdot 6)$ | $6^{(3+5)}$ | $6^8$ |
| $n^2 \cdot n^4$ | $(n \cdot n) \cdot (n \cdot n \cdot n \cdot n)$ | $n^{(2+4)}$ | $n^6$ |
Multiplying Exponents – Summary
Key Points from This Text:
- When multiplying exponents with the same base, the rule is to keep the base and add the exponents. This is demonstrated by expanding the exponents and observing how the base is multiplied repeatedly.
- In cases of different bases, each base and its exponent are calculated separately, and then their results are multiplied. This rule emphasizes that the addition of exponents applies only to like bases.
- The Power of a Power rule states that when an exponent is raised to another power, the exponents are multiplied. This simplifies expressions like $(n^a)^b) to (n^{a \cdot b}$.
- When dealing with exponents inside parentheses, solve the expression within the parentheses first before applying the outer exponent.
- Understanding and mastering these rules of exponent multiplication is crucial for progress in algebra, higher mathematics, and various real-world applications.
- The ability to manipulate and simplify expressions with exponents forms a foundational skill set in mathematical problem-solving and reasoning.
If you want to learn more exponent rules, check out this video Product and Quotient of Powers Laws. Feel free to complete interactive practice problems on this topic or complete our worksheets.
Multiplying Exponents – Frequently Asked Questions
Multiplication with Exponents exercise
-
Write an expression in exponential notation in expanded form.
HintsThe base is the larger number, and the exponent is the smaller number on the top.
The base is the number being multiplied by itself, and the exponent tells how many times the base is used as a factor in the multiplication.
Expanding an exponent means expressing it as repeated multiplication. For instance, for $a^n$, with $a$ as the base and $n$ as the exponent, you expand it by writing $a$ multiplied by itself $n$ times. Thus, $a^n$ expands to $a \cdot a \cdot \ldots \cdot a$, with $a$ appearing $n$ times.
Solution$(3 \cdot 3 \cdot 3 \cdot 3) \cdot (3 \cdot 3)$
-
Determine the rule for multiplying exponents.
HintsThe Law of Exponents for multiplying says that when you multiply two numbers with the same base, you add their exponents together and keep the base the same. For example, $a^m \times a^n = a^{m+n}$, where $a$ is the base and $m$ and $n$ are the exponents.
Expanding the expressions can help you understand why we keep the base and add the exponents when multiplying exponents with the same base.
SolutionThe expression is written in exponential notation. Both terms have the same base of $\bf{3}$, but they have different exponents. The rule for multiplying exponents is to keep the base the same and add the exponents.
The base will remain $3$, and the sum of exponents will be found to find the solution exponent.
The final answer will be $\bf{3^6}$.
-
Simplify an expression using the laws of exponents.
HintsExpanding an exponent means writing it out as repeated multiplication. For example, if you have $a^n$, where $a$ is the base and $n$ is the exponent, you expand it by writing $a$ multiplied by itself $n$ times. So, $a^n$ becomes $a \times a \times \ldots \times a$, with $a$ appearing $n$ times.
There are 4 correct solutions.
Solution$(4^2) \cdot (4^4) = 4^{2+4}$
$(4^2) \cdot (4^4) = (4 \cdot 4) \cdot (4 \cdot 4 \cdot 4 \cdot 4)$
$(4^2) \cdot (4^4) = 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4$
$(4^2) \cdot (4^4) = 4^{6}$
-
Apply the law of exponents to evaluate expressions in exponential notation.
HintsThe Law of Exponents for multiplying says that when you multiply two numbers with the same base, you add their exponents together and keep the base the same. For example, $a^m \times a^n = a^{m+n}$, where $a$ is the base and $m$ and $n$ are the exponents.
Here is another example to help you!
$(1^3) \cdot (1^8)$
$1^{3+8}$
$1^{11}$
Solution$(6^3) \cdot (6^3) = 6^{3+3} = 6^6$
$(6^3) \cdot (6^6) = 6^{3+6} = 6^9$
$(3^3) \cdot (3^3) = 3^{3+3} = 3^6$
$(3^2) \cdot (3^1) = 3^{2+1} = 3^3$
-
What is the rule for multiplying exponents?
HintsThe Law of Exponents for multiplying says that when you multiply two numbers with the same base, you add their exponents together and keep the base the same. For example, $a^m \times a^n = a^{m+n}$, where $a$ is the base and $m$ and $n$ are the exponents.
It may help you to expand each expression that is written in exponential notation. This will explain why we keep the base, and add the exponents.
SolutionThe base is $\bf{8}$ and this number will stay the same.
The exponents, $3$ and $2$ will be added $\bf{3+2}$.
$8^{3+2}$ which can simplify to $8^5$
-
Use the laws of exponents to simplify an expression in exponential notation.
HintsThe Law of Exponents for multiplying states that when you multiply two numbers with the same base, you add their exponents and keep the base unchanged, expressed as $a^m \cdot a^n = a^{m+n}$. This rule can be proven by expanding each exponent into repeated multiplication and observing that the total number of multiplications equals the sum of the exponents.
You can only use the multiplication of exponents rule, $a^m \cdot a^n = a^{m+n}$, when the bases are "like" or the same. If the bases are different, this rule does not apply.
Solution$5^3 \cdot 3^5 \cdot 5^4 \cdot 3^2$
Separate the terms by like bases.
$5^3 \cdot 5^4 = 5^7$
$3^5 \cdot 3^2 = 3^7$
$5^7 \cdot 3^7$ is the final solution because we can not combine these since the bases are unlike.

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
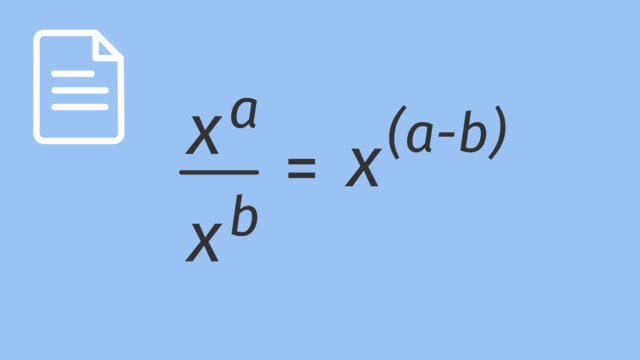
Division with Exponents
How to Convert Decimals Expansions
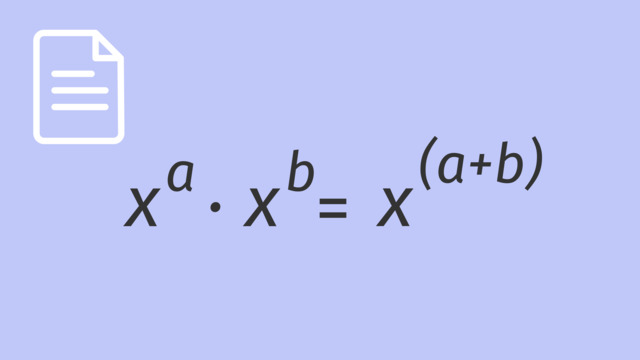
Multiplication with Exponents
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems













