Rational and Irrational Numbers
Basics on the topic Rational and Irrational Numbers
Rational and Irrational Numbers – Definition
In our daily lives, we encounter various types of numbers, from the price of an item to measuring distances. Some of these numbers can be expressed as a fraction of two integers, known as rational numbers, while others cannot and are known as irrational numbers.
Understanding Rational and Irrational Numbers – Differences
Rational numbers include fractions, integers, and perfect squares, while examples of irrational numbers include non-perfect square roots and the number pi ($\pi$).
Rational numbers are neat - you can write them as simple fractions. They include whole numbers and decimals that end or repeat. Irrational numbers are different. They can't be written as simple fractions and their decimals go on forever without repeating. They're like the endless, unique numbers you get from square roots and special math constants.
Rational and Irrational Numbers – Exercises
Let’s look at how to classify numbers as rational or irrational and locate them on a number line.
Rational and Irrational Numbers – Summary
Key Learnings from this Text:
- Rational numbers can be expressed as fractions with both numerator and denominator as integers.
- The decimal representation of rational numbers either ends or repeats.
- Irrational numbers cannot be written as a simple fraction, and their decimal form does not repeat or terminate.
- Identifying and classifying numbers correctly is essential for mathematical calculations and real-world applications.
| Category | Definition | Examples |
|---|---|---|
| Rational | Numbers that can be expressed as a fraction of two integers, where the denominator is not zero. | $\frac{1}{2}$, $0.75$, $\frac{4}{5}$, $2$, $-3$ |
| Irrational | Numbers that cannot be expressed as a simple fraction. Their decimal expansion is non-repeating and non-terminating. | $\sqrt{2}$, π, $\sqrt{3}$, $5.63094…$ |
This video is helpful for more information on the different Types of Numbers you will encounter in life!
Rational and Irrational Numbers – Frequently Asked Questions
Transcript Rational and Irrational Numbers
Are you ready for the math joke of the day? How do rational and irrational numbers communicate? Well, before we can answer that joke, let's make sure we know what these types of numbers are. Rational numbers can be written as a fraction with two integers, where the denominator is not equal to zero. If there is a decimal, it either terminates, which means to end, or the decimal repeats. Here are some examples of rational numbers. Irrational numbers cannot be written as a fraction, and their decimals are non-repeating and non-terminating. Here are some examples of irrational numbers. So, how do rational and irrational numbers communicate? Rational numbers get to the point, while irrational numbers just go on forever... and ever... and ever! Now that that's answered, let's practice identifying some numbers as either rational or irrational. Is five-eighths a rational or irrational number? Since the number is written as a fraction using two integers, it is a rational number. Even if we divide five by eight, it would result in this, which is still rational since the decimal terminates at the thousandth place. Is the square root of ten considered rational or irrational? It is equal to this value and because it goes on forever and there is no repeating pattern, it is an irrational number. Pause the video here and sort this list of numbers into two categories: rational and irrational. Pi is an irrational number because it is a decimal that is non-terminating and non-repeating. One-sixth is a rational number since it is a fraction comprised of two integers. The number negative nine and two-hundredths is also considered rational because we have a decimal that terminates. Evaluating the square root of seven results in a non-repeating, never-ending decimal, making it an irrational number. Negative radical four is equal to negative two, so it is a rational number. The last number is a non-repeating decimal that does not have an end as noted by the ellipsis, or the three dots, which makes it irrational. Let's review. Numbers can be classified as either rational or irrational. In order to identify which category they belong to, you must determine if they can be written as a fraction, and then observe their decimal numbers to see if they repeat or terminate. Both types of numbers are commonly seen in the real world, even if you are looking to bake a new recipe for double chocolate chip cookies or build a new world in a video game you may encounter rational and irrational numbers. Math will always have its rational side where everything is in harmony, but with irrational numbers, it's always an endless adventure!
Rational and Irrational Numbers exercise
-
Find the rational numbers.
HintsA rational number:
- can be written as a fraction
- can be a decimal which terminates or repeats.
A decimal which terminates is rational.
A decimal which does not terminate is irrational.
There are $3$ correct answers here.
SolutionRational numbers are:
- $\mathbf{\frac{1}{4}}$
- $\mathbf{\frac{5}{6}}$
- $2.56$
-
Find the irrational numbers.
Hints$\sqrt{9} = 3$ and $-3$
Therefore, this is a rational number.
If the square root does not terminate or repeat, it is irrational.
An example of an irrational number is $\sqrt{7}$.
As a decimal it is $2.6457513......$ and does not terminate.
There are 3 irrational numbers here.
SolutionThe irrational numbers are:
- $\sqrt{3}$
- $\sqrt{5}$
- $\sqrt{2}$
$\sqrt{4} = 2$ and $-2$
$\sqrt{9} = 3$ and $-3$
They both terminate and therefore they are rational.
-
Order the irrational numbers.
HintsFirst, work out the square roots so you have all the choices as non-terminating decimals.
This will make it easier to determine the smallest value when they are in the same format.
Line up the decimals when they are all in the same format as it is easier to see the values.
For example, like this.
Order the numbers from smallest to largest.
Solution- $1.05729.....$
- $\sqrt{2} = 1.4142...$
- $1.939572....$
- $\sqrt{7} = 2.645...$
- $2.804382...$
-
Which irrational number fits?
HintsStart by matching up the non-terminating decimals.
This will make it easier to see what is left.
For example, if we were looking for an irrational number between $7$ and $8$, we could pair it with $7.3498234$.
When you have matched up the non-terminating decimals, work out the square roots to see if any fit.
For example, an irrational number between $4$ and $5 = \sqrt{17}$.
$\sqrt{17} = 4.12310....$
SolutionIrrational numbers between:
- $2$ and $3 = \sqrt{5} = 2.23606...$
- $3$ and $4 = \sqrt{11} = 3.31662...$
- $4$ and $5 = 4.826936...$
- $5$ and $6 = 5.0403729...$
-
Find the fraction and decimal pairs.
HintsTo match these up we divide the fraction.
For example, $\frac{1}{3} = 1\div3 = 0.3333...$
To convert a fraction to a decimal we divide the numerator by the denominator.
SolutionWe find the decimal by dividing the fraction.
Numerator divided by denominator.
For example, $\frac{13}{99} = 13\div99 = 0.1313...$
-
Solve the equation.
HintsStart by solving the equation, like this.
Solve the equation to get the value of $n$.
Calculate the decimal of $\sqrt{11}$ and decide if it is rational or irrational.
SolutionThe $3$ answers are:
- $\sqrt{11}$
- $3.3166...$
- Irrational

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
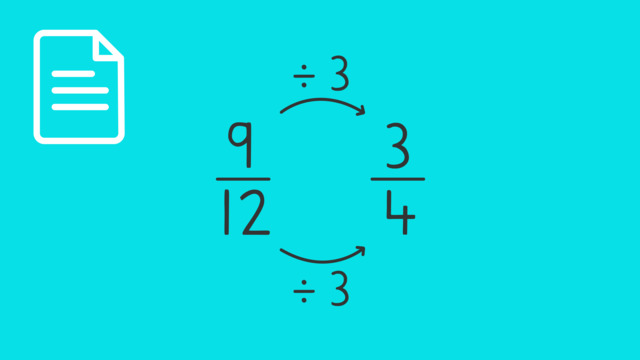
Simplifying Fractions

Temperature Conversion

Decimal Expansions
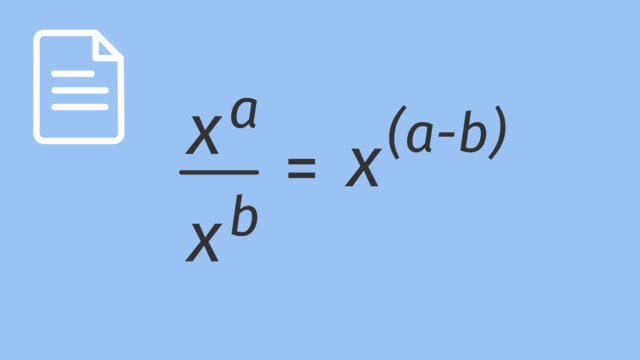
Division with Exponents
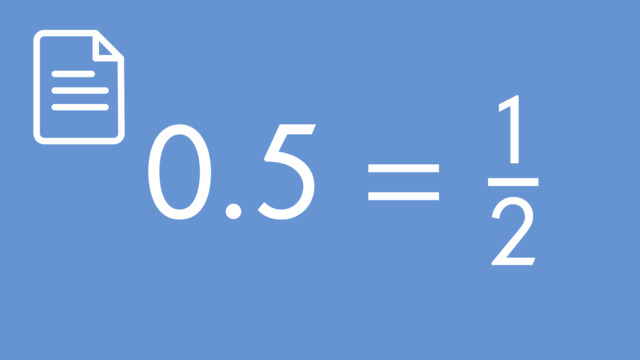
How to Convert Decimals Expansions
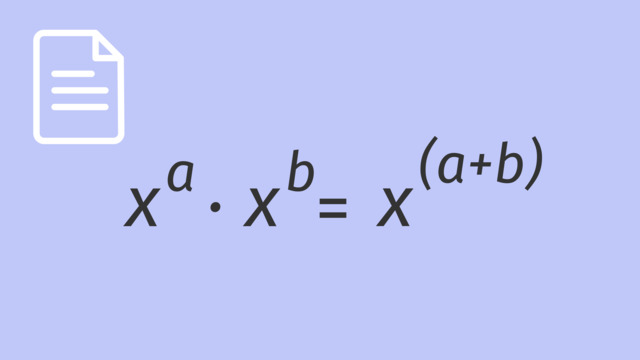
Multiplication with Exponents
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems












