Prime Factorization
- Introduction to Prime Factorization
- Prime Factorization – Definition
- Techniques for Finding Prime Factors
- Applications of Prime Factorization
- Finding the Greatest Common Factor (GCF)
- Determining the Least Common Multiple (LCM)

Basics on the topic Prime Factorization
Introduction to Prime Factorization
Prime factorization is a fundamental concept in arithmetic, where numbers are broken down into their most basic building blocks — prime numbers. It plays a crucial role in various areas of mathematics including algebra, factorization techniques, and number theory.
Prime Factorization – Definition
Prime numbers are the atoms of the numerical world, unique because they can only be divided cleanly by one and themselves.
Prime factorization is the process of expressing a composite number as a product of its prime factors.
To effectively utilize prime factorization, it's essential to understand what primes are and how to identify the factors of a number.
Techniques for Finding Prime Factors
There are several methods to determine the prime factors of a number. Two popular techniques are factor trees and the division method.
Factor Trees are visual representations that help break down a number into its prime factors. Here's a step-by-step guide:
The division method is another systematic way to find prime factors by dividing the number by the smallest possible prime number and continuing the process with the quotient until it's a prime number.
Applications of Prime Factorization
Prime factorization is not just an academic exercise; it has practical applications, such as finding the greatest common factor (GCF) and determining the least common multiple (LCM).
Finding the Greatest Common Factor (GCF)
Finding the Greatest Common Factor is used for simplifying fractions or solving problems involving shared quantities.
Determining the Least Common Multiple (LCM)
Finding the Least Common Multiples is useful when solving problems that require a common denominator or coordinating events.
Prime Factorization – Summary
Key Learnings from this Text:
- Prime factorization is the decomposition of a number into its prime factors.
- Prime numbers are uniquely divisible only by 1 and themselves.
- Factor trees and division methods are effective techniques for finding prime factors.
- Prime factorization is applicable in algebra, helping to simplify expressions and solve equations.
- In arithmetic, prime factorization is used to find the GCF and LCM of numbers.
Practicing prime factorization can lead to a stronger understanding of numbers and their properties.
Prime Factorization – Frequently Asked Questions
Transcript Prime Factorization
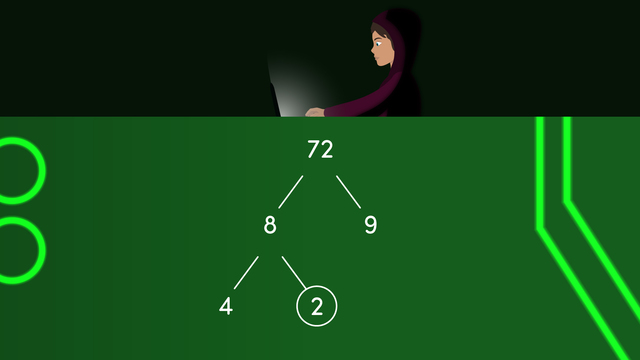
Prime factorization. In our interconnected digital world, where every keystroke echoes through the vast expanse of cyberspace, we walk a challenging tightrope, exposing ourselves to the ever-lurking shadows of hackers, ready to exploit our vulnerabilities and breach the walls of our digital existence. Cryptography protects our data by encrypting codes. Prime factorization is a mathematical concept that helps with encryption, making it difficult for others to break those secret codes. Remember, we classify natural numbers as either composite or prime. Prime factorization is finding which prime numbers multiply together to make the original number. We can organize this process by creating a factor tree. A factor tree is a visual representation that helps us find the prime factors of a number. It is a way to break down a number by repeatedly dividing it into smaller factors. Let's use the number twenty-four as an example. To find the prime factorization of twenty-four, we look for the prime numbers that can be divided evenly into it. We can start by dividing it by the smallest prime number, which is two. Two times twelve makes twenty-four, so we write that here. Since two is prime, we can circle the number to stop here. Let's continue to divide twelve with two and six. Circle this two, and continue to divide six. The two and three will go here, and since they are prime, we will circle them. There are no more composite numbers, so we will list all the prime numbers in sequential order. Twenty-four is equal to two times two, times two, times three. Let's practice with the number, seventy-two. What are two factors of seventy -two? Eight and nine. Let's start with eight. What two factors make eight? Four and two. Two is prime, so we'll circle it and stop. Four is further broken down into two and two. Now, move over to nine. We have three and three, so we can circle and stop. List all the prime numbers in order. Seventy-two is equal to two times two times two times three times three. As you can see, prime factorization can get really long. We can write these expressions in a shorthand way, using exponents. Two is multiplied three times, so we can rewrite it as two to the third power, and the three is multiplied twice, so we can put three to the power of two. Here's one to try on your own. Find the prime factorization of ninety, and write the final expression using exponents if needed. Pause the video for extended time and resume when you're ready to review. There are several factors that you could choose to start with, but we will begin with nine times ten. Nine is made by three and three, which are both prime. And ten is made by two and five, also both prime, so we can stop here. Our prime numbers are two, three, three, and five, which we can write as two times three to the second power times five. Prime factorization is finding which prime numbers multiply together to make the original number. We can use prime factorization to simplify fractions, find the greatest common factor or least common multiple of numbers, test larger numbers for divisibility, and protect our data across the internet.
Prime Factorization exercise
-
Define the keywords for prime factorisation.
HintsExamples of prime numbers: $2, 3, 5, 7, 11, ...$
How many factors does each of these numbers have?
Examples of composite numbers: $4, 6, 8, 9, ...$
How many factors does each of these numbers have?
$110 = 2 \times 5 \times 11$ is an example of prime factorisation.
SolutionA prime number has only two factors; 1 and itself.
A composite number has more than two factors.
Prime factorisation means to write a number as a product of its prime factors.
A factor tree is a diagram used to find the prime factors of a number.
-
Find the prime factorisation for 18.
HintsTo start our prime factorisation we want to find two numbers that multiply to make 18.
Once we have two numbers we draw them on to our factor tree. Now check, are they prime?
If they are prime we circle them and stop that branch, if they are composite we repeat the first two steps until the ends of each branch are prime factors.
There are two correct answers.
SolutionWe can choose any two numbers that multiply to make $18$ to start our prime factorisation so we have two possible answers here.
- $18 = 3 \times 6$,
- $6$ is not prime so we continue,
- $6 = 3 \times 2 $,
- $18 = 2 \times 9$,
- $9$ is not prime so we continue,
- $9 = 3 \times 3$,
-
Complete the prime factorisation for each number.
HintsFirst, draw a factor tree, here is the factor tree for 24 to help you.
The numbers must be in numerical order i.e. smallest to largest.
SolutionHere is the factor tree for $44$
From this we can see that $\bf{44 = 2 \times 2 \times 11}$
_______________________________________________________
- $\bf{26 = 2 \times 13}$
- $\bf{27 = 3 \times 3 \times 3}$
-
Work out the prime factorisation for each number.
HintsUse a factor tree to help you, start by finding numbers that multiply to make the starting number.
For example, the factor tree for $24$ looks like this.
The circled numbers are your prime factors. Don't forget to write the numbers in numerical order, i.e. from smallest to largest.
SolutionIn the image we can see the factor tree for $90$
- $\bf{90 = 2 \times 3 \times 3 \times 5}$
- $\bf{28 = 2 \times 2 \times 7}$
- $\bf{165 = 3 \times 5 \times 11}$
-
True or False?
HintsA number is in prime factorisation form if it is written as a product of its prime factors. Product means multiply.
We continue until all of the factors are prime. The first ten prime numbers are $2, 3, 5, 7, 11, 13, 17, 19, 23, 29$.
Remember you can use a factor tree to help you. The image shows a factor tree for $18$.
First we used $18 = 3 \times 6$.
$3$ is prime so circle $3$ and that branch ends there.
$6$ is not prime so we continue. $6 = 2 \times 3$, these are both prime so we circle those and stop.
Now we know $18 = 2 \times 3 \times 3$ or in index form $18 = 2 \times 3^2$.
Be careful, $9$ is not a prime number because $9 = 3 \times 3$.
There are two correct answers.
Solution$8 = 3 + 5$ is false because this uses addition instead of multiplication.
$42 = 2 \times 3 \times 7$ is true.
$35 = 5 \times7$ is true.
$36 = 2 \times 2 \times 9$ is false because $9$ is not prime.
-
What is the prime factorisation of $1{,}260$?
HintsThere are many ways to start the factor tree. We can start with $\bf{1{,}260 = 126 \times 10}$ or we can start with $\bf{1{,}260 = 2 \times 630}$.
Keep going until each branch ends with a prime number i.e. $2, 3, 5, 7, 11$ etc.
We can write our prime factorisation using exponents (index form).
$\bf{12 = 2 \times 2 \times 3}$ can also be written as $\bf{12 = 2^2 \times 3}$.
SolutionHere are two possible ways to create the factor tree for $1{,}260$, the factor trees may be different but the prime factorisation is the same for any correct factor tree for $1{,}260$.
$\bf{1{,}260 = 2 \times 2 \times 3 \times 3 \times 5 \times7}$.
This can also be written as $\bf{1{,}260 = 2^2 \times 3^2 \times 5 \times7}$.

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples

Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
Division with Exponents
How to Convert Decimals Expansions
Multiplication with Exponents
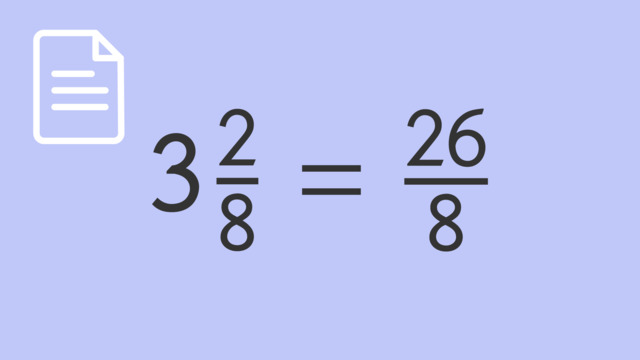
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems









