Product and Quotient of Powers Laws
- Product and Quotient of Powers Laws
- Product and Quotient of Powers Laws – Explanation
- Multiplying Powers with the Same Base
- Dividing Powers with the Same Base
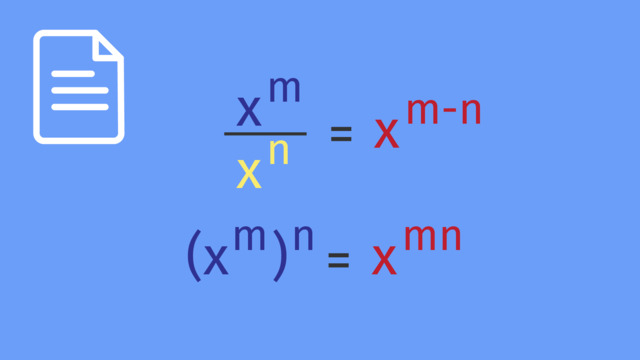

Basics on the topic Product and Quotient of Powers Laws
Product and Quotient of Powers Laws
In mathematics, particularly in algebra, understanding how to manipulate exponents is crucial. Two fundamental rules that we often use are the Product of Powers Law and the Quotient of Powers Law. These laws help simplify expressions and solve equations that are written with exponential notation.
Product of Powers Law states that when you multiply two powers with the same base, you add their exponents. Conversely, the Quotient of Powers Law states that when you divide two powers with the same base, you subtract the exponents of the divisor from the exponents of the dividend.
Product and Quotient of Powers Laws – Explanation
To get a better handle on these laws of exponents, it's really useful to know why multiplying and dividing them works the way it does. Let’s take a closer look at the ideas behind the Product and Quotient of Powers Laws by breaking down what happens when we expand these expressions.
Multiplying Powers with the Same Base
Consider the multiplication of powers with the same base, like $n^{3} \times n^{2}$.
- Expanding: This expression means $n \times n \times n$ (which is $n^{3}$) multiplied by $n \times n$ (which is $n^{2}$).
- Counting the Multiplications: We have 3 $n$'s in the first term and 2 $n$'s in the second term, totaling 5 $n$'s.
- Applying the Product of Powers Law: Thus, $n^{3} \times n^{2}$ simplifies to $n^{5}$, which represents $n$ multiplied by itself 5 times.
Practice applying this concept on your own.
Dividing Powers with the Same Base
Now, let's examine dividing powers with the same base using the example $m^{5} \div m^{2}$.
- Expanding: $m^{5}$ represents $m \times m \times m \times m \times m$, and $m^{2}$ is $m \times m$.
- Visualizing Division: When dividing $m^{5}$ by $m^{2}$, you're essentially canceling out 2 of the $m$'s in $m^{5}$.
- Applying the Quotient of Powers Law: What remains is $m \times m \times m$, which is $m^{3}$. So, $m^{5} \div m^{2}$ simplifies to $m^{3}$.
Practice applying this concept on your own.
Power of a Power
The Power of a Power Law is used when you have a power raised to another power. The rule is simple: multiply the exponents.
Simplify: $(x^{2})^{3}$.
- Expanding: This is $x^{2}$ raised three times, which is $x^{2} \times x^{2} \times x^{2}$.
- Multiplying Exponents: Multiply the exponents $2$ and $3$ to get $x^{6}$.
Try these exercises to understand better.
Power of a Product
The Power of a Product Law applies when a product of bases is raised to a power. You distribute the power to each base.
Simplify $(xy)^{3}$
- Applying the Law: Raise both $x$ and $y$ to the third power, resulting in $(x^{3})(y^{3})$.
Try these exercises on your own.
Power of a Quotient
The Power of a Quotient Law is applied when a quotient is raised to a power. Like the Power of a Product, you distribute the power to both the numerator and the denominator.
Simplify $(\frac{x}{y})^{2}$
- Applying the Law: Raise both $x$ and $y$ to the second power, resulting in $\frac{x^{2}}{y^{2}}$.
Practice with these examples.
Product and Quotient of Powers Law – Application
Understanding the proofs of laws of exponents helps simplify and solve problems with ease. Practice applying each of these rules by simplifying the problems here.
Product and Quotient of Powers Law – Summary
Key Learnings from this Text:
- Exponent rules streamline complex mathematical operations, turning confusing calculations into manageable steps.
- Understanding these laws is crucial for algebraic problem-solving, and it simplifies working with powers and exponents.
- These rules offer a consistent approach, ensuring accuracy and efficiency in solving a wide range of mathematical problems.
- Familiarity with these laws aids in recognizing patterns and relationships in numbers, enhancing overall mathematical comprehension.
- Applying these exponent laws strategically can significantly reduce computation time and complexity in algebra and beyond.
Table of Laws:
| Law | Expression | Result |
|---|---|---|
| Product of Powers | $a^{m} \times a^{n}$ | $a^{{m+n}}$ |
| Quotient of Powers | $\frac{a^{m}}{a^{n}}$ | $a^{{m-n}}$ |
| Power of a Power | $(a^{m})^{n}$ | $a^{{mn}}$ |
| Power of a Product | $(ab)^{n}$ | $a^{n} \times b^{n}$ |
| Power of a Quotient | $\left(\frac{a}{b}\right)^{n}$ | $\frac{a^{n}}{b^{n}}$ |
Product and Quotient of Powers Law – Frequently Asked Questions
Transcript Product and Quotient of Powers Laws
Archimedes is deep in thought in his seaside garden in ancient Greece. He's contemplating how many grains of sand it would take to fill the universe. While he's pondering, he notices a small child placing stones in a rectangular pattern. Eureka! The space filled with stones represents a small piece of the universe. Perhaps Archimedes can learn something here. Because the universe is exponentially large. Archimedes can use the Product and Quotient of Powers Laws to solve this mystery. Archimedes counts the stones in the pattern. The length of the first side is 8 stones. And the length of the second side is 16 stones. But what's that? For the first side, he hears the child counting two... times two... times two. And for the second side, two times two times two times two. The child is counting the stones by multiples of two! Like Archimedes, we already know that we can represent repeated multiplication with exponents. So, when we multiply 2 by itself three times, we can write that as 2 to the third power. And for the second side, 2 times itself 4 times equals 2 to the fourth power. How many stones would the child need to fill the entire rectangular area? To find out, we'd need to calculate the area by multiplying one side length by the other. That gives us 2 cubed times 2 to the fourth. To multiply powers with like bases lets first rewrite them in factored form. This means we have two times itself three times multiplied by two times itself four times. How many twos is that? We see that this expression is just 2 multiplied by itself 7 times. This can be written as 2 to the 7th power. Do you notice any relationship between the original exponents of 3 and 4 with the final exponent of 7? Well, adding together the exponents 3 and 4 gives us the sum of 7. Hmm, interesting. Archimedes decides to use this reasoning to further understand his grains of sand problem. He estimates the amount of sand in his rectangular garden to be 10 to the 5th times 10 to the 3rd. Again, let's write each term in factored form. Notice that we have 10 times itself 8 times. This can be written as 10 to the 8th power. What about the relationship between the original exponents of 5 and 3 with the final exponent of 8? Looks like when we multiply powers with the same base we can just add their exponents. This brings us to an important law of exponents called the Product of Powers law. Based on the patterns we've seen, we know that when we multiply powers with like bases, we can add together the exponents. This law holds true for all numbers and can help us simplify expressions of this case. But what happens when we divide like bases? Let's take a look at the fraction 3 to the fifth divided by 3 squared. To simplify this expression, we can write the numerator in factored form and the denominator in factored form. Remember, with fractions we can cancel out common factors. What are we left with? This results in 3 to the third power, also known as 3 cubed. Do you have a hypothesis about where that exponent of 3 came from? Well subtracting the exponents seems to give us the answer. Let's try one more example just to make sure. How about the expression 8 to the 6th power, divided by 8? Remember, any number can be written with an exponent of one, because it just means that number is there one time. Again, let's factor each term... then cancel out common factors. Does your hypothesis still hold true by subtracting the exponents? Yes, when we divide powers with like bases we subtract their exponents. This is called the Quotient of Powers law, and it's a close cousin to the Product of Powers law you just learned. It also works for all numbers except here we are dealing with fractions so 'x' cannot be zero. Let's review our findings. The product of powers law states when multiplying together powers with the same base you can add the exponents together to simplify the expression. While the quotient of powers law states when dividing powers with the same base you can subtract the exponents to simplify the expression. Remember that the base can't be zero in the quotient of powers law. With this knowledge Archimedes finds out that 10 to the 51st grains of sand fit in a sphere that would make up our universe. That's one, zero, zero, zero, zero, zero, zero, zero, zero, zero, zero,…
Product and Quotient of Powers Laws exercise
-
Identify an equivalent expression using your understanding of the Product of Powers Law.
HintsMake sure you remember to follow the Product of Powers Law. When multiplying powers with the same base, keep the base, and add the exponents.
When answering multiple choice questions, check each solution to make sure you are confident with your answer!
Here is a similar example to help you understand.
The expression $8^8$ is equivalent to $8^2\cdot8^6$.
Solution$10^{25}\cdot10^{26}=10^{51}$
Since the bases are the same, the exponents can be added together to find the solution, which is 51
-
Explain the Laws of Exponents pertaining to multiplication and division.
HintsThe Product of Powers Law states that if you have the same base and are finding a product, the base stays the same, and the exponents can be added.
The Quotient of Powers Law states that if you have the same base and are finding a quotient, the base stays the same, and the exponents can be subtracted.
SolutionThe law called Products of Powers states that when multiplying exponents that have the same base, the base will stay the same, and then add the exponents.
For example, $(x^6)\cdot(x^2)$ has the same base of $x$. We can add the exponents, $\bf{6+2}$ to find that our exponent will now be $\mathbf{8}$.
$(x^6)\cdot(x^2)$ = $\bf{x^8}$
The law called Quotient of Powers states that when dividing exponents that have the same base, the base will stay the same, and then subtract the exponents.
For example, $\dfrac{x^6}{x^2}$ has the same base of $x$. We can subtract the exponents, $6-2$ to find that our exponent will now be $\bf{4}$.
$\dfrac{x^6}{x^2}$ = $\bf{x^4}$
-
Interpret expressions written in exponential notation while applying the laws of exponents.
HintsRewriting exponential notation in factored form can help us understand the Product of Powers law.
$(y^2) \cdot (y^4) = (y \cdot y) \cdot (y \cdot y \cdot y \cdot y)$
Notice, that when the expression is factored, or expanded, there are a total of six $y$ s.
Rewriting exponential notation in factored form can help us understand the Quotient of Powers law.
$\dfrac{y^4}{y^2} = \dfrac{y \cdot y \cdot y \cdot y}{y \cdot y}$
Notice, that when the expression is factored, or expanded, there are a total of four $y$ s in the numerator and two $y$ s in the denominator.
SolutionThe following expressions are equal to $2^4$:
$(2^2)\cdot(2^2)$
$(2^0)\cdot(2^4)$
$\frac{2^8}{2^4}$
$(2\cdot2\cdot2)\cdot(2)$
The following expressions are equal to $2^5$:
$(2^3)\cdot(2^2)$
$(2^4)\cdot(2^1)$
$\frac{2^9}{2^4}$
$(2\cdot2\cdot2)\cdot(2\cdot2)$
-
Apply the Laws of Exponents to simplify the expressions.
HintsRemember, when you are multiplying powers with like bases, keep the base, and add the exponents together.
$(w^2)\cdot(w^3) = w^{(2+3)} = w^5$
Remember, when you are dividing powers with like bases, keep the base, and subtract the exponents.
$\frac{d^7}{d^3} = d^{(7-3)} = d^4$
Solution$(m^6)\cdot(m^7) = m^{13}$
$(m)\cdot(m^3) = m^4$
$(m^2)\cdot(m^7) = m^9$
$\dfrac{m^7}{m^2} = m^5$
$\dfrac{m^9}{m^6} = m^3$
$\dfrac{m^7}{m^6} = m$
-
Simplifying expressions in exponential notation using the Product of Powers Law.
HintsThe Product of Powers Law states that when multiplying powers with the same base, follow these steps:
- Keep the base the same.
- Add the exponents together.
Here is an example on how to apply the Product of Powers Law.
$(g^3)\cdot(g^7)$
$g^{(3+7)}$
$g^{10}$
To find the product of powers, we can keep the base the same, $x$, and add our exponents together, $3+5$.
Solution$(x^3)\cdot(x^5) = \bf{x^{8}}$
Keep the base $x$ and add the exponents $3+5$.
-
Apply your knowledge of the Laws of Exponents to simplify expressions.
HintsFirst, simplify each numerator and denominator separately.
Apply your knowledge of the Product of Powers Law.
$n^6\cdot n^2=n^{6+2}=n^8$
If it helps you visualize better, expand (or write in factored form) both the numerator and the denominator.
Expanding looks like this:
$n^6\cdot n^2 = (n\cdot n\cdot n\cdot n\cdot n\cdot n) \cdot (n\cdot n)$
$\dfrac{(x)\cdot(x^5)}{(x^2)\cdot(x^3)}$
This can be expanded to look like this:
$\dfrac{(x)\cdot(x\cdot x\cdot x\cdot x\cdot x)}{(x\cdot x)\cdot(x\cdot x \cdot x)}$
Now the $x$'s can be canceled out.
$x^1=x$
Solution$\dfrac{(n^2)\cdot(n^6)}{(n^3)\cdot(n)}$
$\dfrac{n^8}{n^4}$
$n^4$








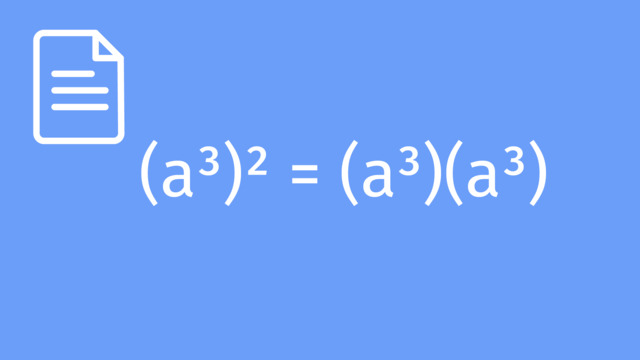















I like that math because it easy when I am 6 years old i like to do math i like it a lot