Comparing Fractions Using Cross Multiplication
- Comparing Fractions Using Cross Multiplication – Explanation
- Comparing Fractions Using Cross Multiplication –- Method
- Comparing Fractions Using Cross Multiplication – Guided Practice 1
- Comparing Fractions Using Cross Multiplication – Guided Practice 2
- Comparing Fractions with Unlike Denominators – Application of the Method


Basics on the topic Comparing Fractions Using Cross Multiplication
Comparing Fractions Using Cross Multiplication – Explanation
We know what a fraction is, and now we are going to learn how to recognize which fraction is smaller or bigger, or in other words, we will learn to compare fractions with same or different denominators.
For example, if we are thinking of an apple and cutting it in half, we know the half is smaller than the whole apple. If we cut the half of the apple again in half, we are going to have a quarter of an apple. Again, the quarter is smaller than the half of an apple.
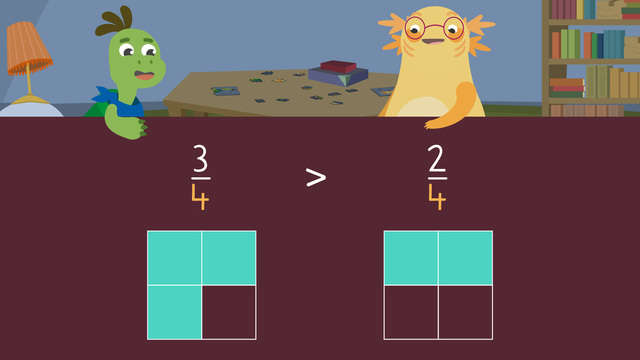
This learning text is about comparing two fractions. In order to compare fractions, we use signs of less than (<) or more than (>) or equal to (=).
Firstly, we will look at the definition of what a fraction is, and then we will engage with the explanation on how to use cross multiplication to compare fractions.
Fractions always represent a part of a whole. For example, if a pizza is divided into four equal pieces, one piece is called $\frac{1}{4}$ of a whole pizza.
Comparing Fractions Using Cross Multiplication –- Method
Cross multiplication is one of the methods to compare fractions. Let’s look at how this method works: To compare two fractions using cross multiplication, we multiply the denominator of one fraction with the numerator of the other fraction. In our example below, we multiplied four by three across.
Then, compare the products to determine if the fraction is less than (<), more than (>) or equal to (=). This time, we have both fractions equal to each other.
Have a look at a few more examples below. You can also check our worksheet on how to use the cross multiply method to compare fractions.
Comparing Fractions Using Cross Multiplication – Guided Practice 1
This time, we are comparing $\frac{2}{3}$ and $\frac{3}{5}$.
Let’s follow the steps we learned about above to compare.
First, multiply the denominator three of the first fraction with the numerator three of the second fraction. The product of this calculation is 9.
Then, multiply the denominator five of the second fraction with the numerator two of the first fraction. The product of this calculation is 10.
Finally, compare the products: ten is greater than nine, so the fraction $\frac{2}{3}$ is greater than the fraction $\frac{3}{5}$.
Comparing Fractions Using Cross Multiplication – Guided Practice 2
In our next example, we are looking at $\frac{5}{14}$ and $\frac{7}{12}$. We are going to follow the same steps as in our first example:
Multiply the denominator fourteen of the first fraction with the numerator seven of the second fraction. The product here will be 98.
Then, multiply the denominator twelve of the second fraction with the numerator five of the first fraction. The product here will be 60.
Finally, compare the products: sixty is less than ninety-eight, so the fraction $\frac{5}{14}$ is smaller than $\frac{7}{12}$.
Comparing Fractions with Unlike Denominators – Application of the Method
Why does the cross multiply work when comparing fractions?
When we compare fractions with different denominators, we must convert both fraction into equivalent fractions with a common denominator. We use cross multiplication in exactly the same way as converting both fractions into equivalent fractions. The only difference is we skipped writing the denominators. The example below shows both ways of comparing fractions –cross multiplication and conversion into equivalent fractions with common denominators. You may have noticed that both of the methods end up with the same products of the numerators: ten and nine, that is why $\frac{2}{3}$ is greater than $\frac{3}{5}$.
Comparing Fractions Using Cross Multiplication – Summary
How do we compare fractions using cross multiply? Look at the summary below:
| Step # | What to Do |
|---|---|
| 1 | Multiply the denominator of the first fraction with the numerator of the second fraction. |
| 2 | Then, multiply the denominator of the second fraction with the numerator of the first fraction. |
| 3 | Finally, compare the products and use the appropriate sign; less than (<), more than (>) or equal (=). |
Now you should be able to compare fractions using cross multiplication. If you need more help, please watch the video and complete interactive exercises or the worksheet on comparing fractions using cross multiply.
Frequently Asked Questions about Comparing Fractions Using Cross Multiplication
Transcript Comparing Fractions Using Cross Multiplication
Axel and Tank are in the treasure hunt room at the Sunken Ship Funhouse. They get five minutes in the room to find as many treasure chests with the greater amounts of jewels as they can. "This one has two-thirds jewels!" "This one has three-fifths! How do we know which one has more?" In order to collect as many jewels as they can, Axel and Tank will be... Comparing Fractions Using Cross Multiplication. When we compare fractions, we are determining which one is greater than, less than, or equal to the other. Cross multiplication is one method used to compare fractions. To compare using cross multiplication, multiply the denominator of one fraction with the numerator of the other fraction being compared. Then, compare the products to determine if the fraction is greater than, less than, or equal to the other. Let’s use the two-thirds and three-fifths fractions as an example. First, multiply THIS denominator, three, by THIS numerator, three. Three times three is nine. Next, multiply THIS denominator, five, across to THIS numerator, two. Five times two is ten. Now, compare the products. Ten is greater than nine… so two-thirds is GREATER than three-fifths. Why does cross multiplication work when comparing fractions? When we compare fractions with different denominators, we look to make equivalent fractions with the same denominator. We find the least common multiple that each denominator shares and multiplying the numerator by that same number. In the fractions two-thirds and three-fifths, the common denominator is fifteen. Since you multiply three times five to make fifteen, multiply the numerator by five. Two times five is TEN. Five times three is fifteen and three times three equals NINE. Ten-fifteenths is greater than nine-fifteenths...so two-thirds is greater than three-fifths. In cross multiplication, the product of each side of the fraction is the SAME as the numerators created in the equivalent fractions. This method is useful when you are working with fractions with larger numbers or have multiple-step problems to solve. Now, let's help Axel and Tank compare more fractions using cross multiplication. Compare seven-ninths and eight-twelfths. What is nine times eight? Seventy-two. What is twelve times seven? Eighty-four. Is seven-ninths less than, greater than, or equal to eight-twelfths? Seven-ninths is GREATER than eight-twelfths. Compare five-fourteenths and seven-twelfths. Pause the video to solve and press play when you're ready to check the solution. Twelve times five is sixty and fourteen times seven is ninety-eight so, five-fourteenths is LESS than seven-twelfths. Looks like time is running out for Axel and Tank's treasure hunt, so let's review. Remember... when we compare fractions, we are determining which one is greater than, less than, or equal to the other. Cross multiplication is one method used to compare fractions. To solve using cross multiplication, multiply the denominator of one fraction with the numerator of the other fraction across the expression. Then, compare the products to determine which fraction is greater than, less than, or equal to the other. This method is useful when you are working with larger fractions or have a multiple-step problem to solve. "Time's up! How do we get out of here?" "This way!"
Comparing Fractions Using Cross Multiplication exercise
-
Label the picture.
Hints2 x 5 = ? 3 x 3 = ?
Which answer is greater?The symbol < means the left is less than the right.
The symbol > means the left is greater than the right.
The symbol = means both the left and right are equal to each other.Solution- To find which fraction is greater, use cross multiplication with the numerators and denominators.
- 2 x 5 = 10, and 3 x 3 = 9.
- 10 is greater than 9, so $\mathbf{\frac{2}{3}}$ is greater than $\mathbf{\frac{3}{5}}$.
-
Complete the steps to compare fractions.
HintsCross multiply the numerator and denominator to find which fraction is greater, lesser, or equal.
Shown below is an example.
$\frac{9}{10}$ ? $\frac{4}{5}$
In order to find which is greater, first solve for 9 x 5 and 10 x 4 as this cross multiplys the numerators and denominators. Once we have the answers we can compare those numbers.
The symbol < means the left is less than the right.
The symbol > means the left is greater than the right.
The symbol = means both the left and right are equal to each other.Solution- To find which number is greater, first multiply the numerator of the left fraction with the denominator of the right fraction.
- Next, multiply the denominator of the left fraction with the numerator of the right fraction.
- Compare the products of the multiplication equations to find which result is greater.
- 45 is greater than 40, so $\frac{9}{10}$ is greater than $\frac{4}{5}$.
-
Match the fractions and expressions.
HintsCross multiply the numerator and denominator to find which fraction is greater than, less than, or equal to.
Shown below is an example.
Example:
- $\frac{4}{9}$ and $\frac{3}{5}$
- 4 x 5 = 20, 9 x 3 = 18
- 20 > 18
- So, $\frac{4}{9}$ > $\frac{3}{5}$
Solution$\frac{9}{10}$ and $\frac{4}{5}$
9 x 5 = 45
10 x 4 = 40
45 < 40$\frac{2}{5}$ and $\frac{7}{9}$
2 x 9 = 18
7 x 5 = 35
18 < 35$\frac{6}{3}$ and $\frac{4}{9}$
6 x 9 = 54
3 x 4 = 12
54 < 12$\frac{2}{10}$ and $\frac{8}{14}$
2 x 14 = 28
10 x 8 = 80
28 < 80 -
Highlight the correct expressions.
HintsCross multiply the numerator and denominator to find which fraction is greater than, less than, or equal to.
Shown below is an example.
The symbol < means the left is less than the right.
The symbol > means the left is greater than the right.
The symbol = means both the left and right are equal to each other.Solution1) 4 x 5 = 20, 6 x 3 = 18. 20 is greater than 18, so $\mathbf{\frac{4}{6}}$ is greater than $\mathbf{\frac{3}{5}}$.
2) 7 x 10 = 70, 9 x 6 = 54. 70 is greater than 54, so $\mathbf{\frac{7}{9}}$ is greater than $\mathbf{\frac{6}{10}}$.
3) 2 x 10 = 20, 3 x 8 = 24. 20 is less than 24, so $\mathbf{\frac{2}{3}}$ is less than $\mathbf{\frac{8}{10}}$.
4) 2 x 10 = 20, 6 x 5 = 30. 20 is less than 30, so $\mathbf{\frac{2}{6}}$ is less than $\mathbf{\frac{5}{10}}$. -
Compare the fractions.
HintsThe symbol < means the left is less than the right.
The symbol > means the left is greater than the right.
The symbol = means both the left and right are equal to each other.In order to find which fraction is greater than, less than, or equal to, cross multiply the numerator and denominator. Then compare the products.
In this example, 10 is greater than 9. So, $\mathbf{\frac{2}{3}}$ is greater than $\mathbf{\frac{3}{5}}$.Solution- $\mathbf{\frac{7}{9}}$ and $\mathbf{\frac{8}{12}}$
- 7 x 12 = 84
- 9 x 8 = 72
- 84 > 72
- $\mathbf{\frac{7}{9}}$ > $\mathbf{\frac{8}{12}}$
-
Complete the blanks with >, =, or <.
HintsCross multiply the numerator and denominator to find which fraction is greater, lesser, or equal.
Example:
- $\frac{4}{9}$ and $\frac{3}{5}$
- 4 x 5 = 20, 9 x 3 = 18
- 20 < 18
- So, $\frac{4}{9}$ > $\frac{3}{5}$
Solution1) $\frac{5}{11}$ and $\frac{2}{3}$
5 x 3 = 15
11 x 2 = 22
15 < 22
$\frac{5}{11}$ < $\frac{2}{3}$2) $\frac{7}{12}$ and $\frac{6}{7}$
7 x 7 = 49
12 x 6 = 72
49 < 72
$\frac{7}{12}$ < $\frac{6}{7}$3) $\frac{16}{20}$ < $\frac{8}{10}$
16 x 10 = 160
20 x 8 = 160
160 = 160
$\frac{16}{20}$ = $\frac{8}{10}$4) $\frac{13}{15}$ < $\frac{8}{9}$
13 x 9 = 117
15 x 8 = 120
117 < 120
$\frac{13}{25}$ < $\frac{8}{9}$