Even and odd numbers


Basics on the topic Even and odd numbers
A number is said to be even if and only if it is divisible by 2; otherwise, it’s said to be odd. Another way to know whether a number is even or odd, simply look at its last digit. If a number ends in 0, 2, 4, 6, or 8, then it’s even, but if it ends in 1, 3, 5, 7, or 9, then it’s odd. For instance, looking at the numbers 125 and 236, we can see that, since 5 is the last digit of 125, it’s odd, while 236 ends in 6, which is divisible by 2, so it’s even. Learn how to identify a number whether it is an even or odd by helping Odd Autumn and Even Steven, the two intrepid friends who are on a quest to the Splitcypress Forest to find a Puffstritch, divide their haul or food evenly. Common Core Reference: CCSS.MATH.CONTENT.4.OA.C.5
Transcript Even and odd numbers
Odd Autumn and Even Steven set out months ago on a quest to the Splitcypress Forest to find a Puffstrich. Every day, they search of food for the night - and every night, the pair divide the day’s haul. In order for these intrepid friends to see if they can share their haul evenly, they need to know about even and odd numbers.
Let’s see what they found today. The two friends empty their carts in a small pile between them. Autumn has 11 charmberries in her cart. Before deciding if they can share the eleven berries evenly, they need to know: Is 11 an even or odd number? Is it divisible by 2?
Understanding divisibility
Before we answer this question, we need to understand divisibility. In math, we say a number is divisible by another number if the quotient, or answer, is a whole number with no remainder. Even numbers are all whole numbers that are divisible by the number 2, while odd numbers are all the rest (not evenly divisible by 2). Autumn takes a look using long division. There’s a remainder of 1! 11 must not be an even number! So, if they share the charmberries evenly, they'll have 1 left.
Determining whether odd or even
But there’s gotta be a quicker way than long division to determine whether or not a number is even or odd. Luckily, Even Steven knows that you only have to look at the last number to determine the parity - the evenness or oddness of a number. If the number ends in a 1, 3, 5, 7 or 9, it's odd. Otherwise, it's even.
Autumn takes out the next items from her cart. Whoa! She’s got 15 mag fruits! She follows Steven’s advice and just looks at the last number - 5. Since the last digit is odd, Autumn reluctantly admits 15 must be odd, too. So, after sharing evenly, they have one left over again.
Now that Odd Autumn’s cart is empty, time to inspect Steven’s cart. Steven produces 128 viviseeds from his cart. Since Steven is so used to just looking at the last number to determine if a number is even or odd, he concentrates on 8. In all his practice, Steven has memorized that the even digits are 0, 2, 4, 6 and 8. Since 8 is the last digit of 128, and it’s in the list he memorized, 128 must be an even number! So they can share the seeds evenly without any leftovers.
Now that the two friends have divided their haul for the day evenly between the two of them, what should they do with the remaining charmberry and mag fruit? Oh look! Finally, a Puffstrich! They’re in luck! It’s been said Puffstriches love charmberries and mag fruits. Maybe this one will want to be their pet.
Even and odd numbers exercise
-
Determine if 11 is odd or even.
HintsAn even number is divisible by 2 and has no remainder.
An odd number has a remainder when it is divided by 2.
SolutionAutumn knows that an even number is divisible by 2, with no remainder. Odd numbers have a remainder when divided by two.
Therefore, Autumn knows that if she divides 11 by 2 she can figure out if the number, 11, is even or odd. She knows that if she gets a remainder, then 11 must be odd. If she gets no remainder, then 11 must be even.
Autumn divides 11 by two using long division. You can see her calculations in the image.
She finds that 11 divided by 2 is 5, with a remainder of 1.
Since there is a remainder of 1, 11 must be odd.
-
Summarize your knowledge about even and odd numbers.
HintsA number is divisible by two, if you get no remainder when you divide that number by two.
Even numbers are divisible by two.
SolutionEven Steven reviews some key facts about even and odd numbers before he starts completing Autumn's statements.
A number is divisible by two if you get no remainder when you divide that number by two.
Even numbers are divisible by two. Odd numbers are not divisible by two.
So Stephen knows that:
"Odd numbers...are all the numbers that are not evenly divisible by two."
"All numbers that...are divisible by two are even numbers."
"Even numbers...are all divisible by two with no remainder."
"Numbers that give a remainder when divided by two...are odd."
-
Determine which numbers are odd and which are even.
HintsIf you divide a number by $2$ and get a remainder, that number is odd.
If you divide a number by $2$ and get no remainder, that number is even.
A number is even if its last digit is a $0$, $2$, $4$, $6$, or $8$.
SolutionIf you divide a number by $2$ and get a remainder, that number is odd. If you divide a number by $2$ and get no remainder, that number is even.
But Even Stephen has a trick: He knows that a number is even if its last digit is a $0$, $2$, $4$, $6$, or $8$. A number is odd if its last digit is $1$, $3$, $5$, $7$, or $9$.
Using Stephen's trick, we can see that:
$6$ pears, $14$ walnuts, and $26$ basil leaves are all even numbers.
$19$ hazelnuts, $7$ apples, and $11$ cherries are all odd numbers.
-
Determine which numbers are even and which are odd.
HintsIf a number ends in $1$, $3$, $5$, $7$, or $9$, then it's odd.
If a number ends in $0$, $2$, $4$, $6$, or $8$, then it's even.
SolutionIf a number ends in $1$, $3$, $5$, $7$, or $9$, then it's odd.
If a number ends in $0$, $2$, $4$, $6$, or $8$, then it's even.
So $283$, $8247$, $921$, and $3011$ are odd.
And we have that $926$, $4822$, $9740$, and $2734$ are even.
-
Explain what it means if a number is divisible by another number.
HintsA number is even if its last digit is a $0$, $2$, $4$, $6$, or $8$.
If a number is divisible by $3$, you get no remainder when you divide that number by $3$.
SolutionIf you divide a number by $2$ and get a remainder, that number is odd, not even.
A number is divisible by two if you get no remainder when you divide that number by two. So the third statement is correct.
A number is even if its last digit is a $0$, $2$, $4$, $6$, or $8$. So the fourth statement is correct.
-
Select the even numbers.
HintsIf a number ends in $1$, $3$, $5$, $7$, or $9$, then it's odd.
If a number ends in $0$, $2$, $4$, $6$, or $8$, then it's even.
SolutionIf a number ends in $1$, $3$, $5$, $7$, or $9$, then it's odd. If a number ends in $0$, $2$, $4$, $6$, or $8$, then it's even. These rules are always true, not matter how many digits a number has.
So out of the given numbers, only the following numbers are even:
$134$ - $624$ - $938$ - $836$
$7298$ - $2084$ - $3942$ - $3094$
$20932$ - $83584$ - $65692$ - $89264$

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
Division with Exponents
How to Convert Decimals Expansions
Multiplication with Exponents
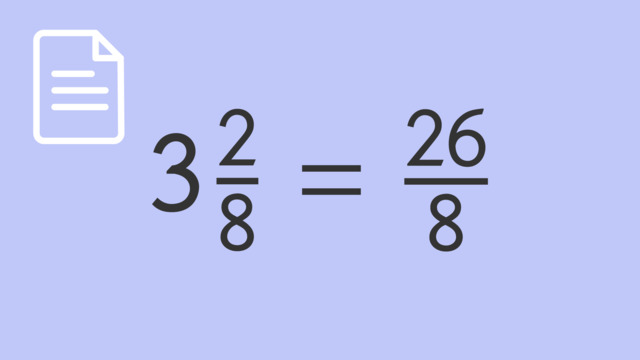
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems












@DAISY, i LOVE cheeseburgers!!! :)
theyre a ship i know it
I have a fun game on my computer.
its called bloxd.io and I love it
who is your fav artist in the renisaunce
hopefully she doesn't find out