Divisibility Rules - 4, 5, 8, 10


Basics on the topic Divisibility Rules - 4, 5, 8, 10
Have you ever wondered why some numbers will divide evenly (without a remainder) into another number, while others will not? Divisibility rules help us determine if a number will divide into another number without actually having to divide. This video shows examples of the divisibility rules for 4, 5, 8, and 10.
The divisibility rules for 4, 5, 8, and 10 are as follows:
The Rule for 4: a number is divisible by 4 if its last two digits are evenly divisible by 4. For example, 2312. The last two digits are 12 and it is divisible by 4. Thus, 2312 is divisible by 4. The Rule for 5: a number is divisible by 5 if it ends with 0 or 5. For example, 3750 and 42755. The two numbers end with 0 and 5. Thus, these numbers are divisible by 5. The Rule for 8: a number is divisible by 8 if the last three digits are evenly divisible by 8. For example, 17216. The last three digits are 216 and it is divisible by 8. Thus, 17216 is divisible by 8. The Rule for 10: a number is divisible by 10 if it ends with 0. For example, 35070. The number ends with 0, therefore the number is divisible by 10.
Note that once a number doesn’t satisfy a rule, then that number is not divisible by the number that rule is for. There is a divisibility rule for every number. However, some of the rules are easier to use than others. For the rest, it might be simpler to actually divide.
Compute fluently with multi-digit numbers and find common factors and multiples.
CCSS.MATH.CONTENT.6.NS.B.4
Transcript Divisibility Rules - 4, 5, 8, 10
Billy Bonka is bonkers for making sweet treats. Customers love his delicious candy concoctions and the latest batch is ready. Billy just needs to divide the batch into packages with 4, 5, 8 or 10 treats.
To figure this out, Billy Bonka can use the rules of divisibility. In his latest batch, Billy made 1516 blueberry balls, 1035 caramel cubes, and 1600 strawberry strips and he has packaging for 4, 5, 8 and 10 treats per package. Billy wants to package the treats without having any remainders, so he must divide the number of treats among the packages evenly. Okay, let’s get to work. Which of the candies can Billy pack into packs of 5?
Divisibility by 5
First, let's list the mutiples of 5. 5, 10, 15, 20, 25, 30 and so on. What do the multiples all have in common? They all end in a 5 or a 0. So, for a number to be divisible by 5, it must end in a 5 or a 0. The number 1516 doesn’t end in a 5 or a zero. So, we can safely tell Billy that 1516 isn't evenly divisible by 5. As for the last two numbers, 1035 and 1600, one ends in a 5 and one ends in a 0, so both numbers must be divisible by 5.
Divisibility by 10
But what if Billy wants to divide the candies into packages of 10? He could figure this out using long division, but there's a faster way to determine if a number is divisible by 10. Because every multiple of 10 ends with a 0a number is divisible by 10 if it also ends with a 0. The number of blueberry balls doesn’t end with a 0, so this number is not divisible by 10.
Divisibility by 4
Maybe Billy can pack the candies into groups of 4? There's a special rule you can use when deciding whether or not a number is divisible by 4, just concentrate on the last two digits! That's right! No matter how long a number is, if the last two digits are divisible by 4, then the whole number is divisible by 4 as well.
Let’s try this out. The last two digits of the number 1516 are 16 and since 16 is evenly divisible by 4, 1516 should be divisible by 4 as well. To check, we can perform long division. 4 goes into 15 three times, bring down the one. 4 goes into 31 seven times, subtract 28 from 31and finally, bring down the 6. Would ya look at that?! 1516 IS divisible by 4!
But why does this work? When dividing by 4, you're really just dividing by 2 twice! Divide by two and then by two again. If the quotient is a whole number, then the dividend is divisible by 4. For 1035, the last two digits are 35. Is 35 evenly divisible by 4? Finally, if the last two digits of the number in question are both 0, then the number is divisible by 4! Pretty easy, right?
Divisibility by 8
But what about packs of 8? Although the rule for 8 might seem a little tricky, it can save you a lot of time. For multiples of 8, if the last three digits are divisible by 8, then the entire number is divisible by 8. Is 516 divisible by 8? 8 goes into 51 six times, bring down the 6 and since 8 doesn't go into 36 an even number of times, 516 isn't evenly divisible by 8 and therefore neither is 1516.
Using the Divisibility Rules
What can Billy do with the 1035 cubes of chewy caramels? Let’s use the divisibility rules to figure it out. The last three digits are 035, and that’s not evenly divisible by 8. Wow that was fast and easy! Like taking candy from a baby! And finally, let's take a look to see if 1600 is divisible by 8.
8 goes into 60 seven times, bring down the 0. No remainder! Since 600 is evenly divisible by 8, 1600 must also be divisible by 8! Earlier, we said that dividing a number by 2 twice is the same as dividing by 4 once. The same concept applies when deciding if a number is divisible by 8. We can divide by 2 three times and if each of the quotients is a whole number, then the original number is divisible by 8!
Summary of Divisibility Rules
So, just to review.
A number is divisible by 10 if it ends with 0 A number is divisible by 5 if it ends with 5 or 0. A number is divisible by 4 if the last 2 digits are evenly divisible by 4 or if it is divisible by 2 twice and the quotient is a whole number. A number is divisible by 8 if the last 3 digits are evenly divisible by 8 or if it is divisible by 2 three times and the quotient is a whole number.
Okay, back to Billy. Billy has it all figured out. He'll have this batch of goodies ready for delivery in no time at all. That's just great! Unless he decides to make combinations packs. Oh boy!
Divisibility Rules - 4, 5, 8, 10 exercise
-
Decide which number is divisible by $4$.
HintsLet's have a look at an example: $1232$
First we divide this number by $2$ to get $616$. Once more we divide it by $2$. The result is $308$.
Let's check the result: $4\times 308=1232$ $~~~~~$✓
$32$ is divisible by $4$ because $32\div4=8$.
Only even numbers are divisible by $2$.
SolutionBecause the multiples of $4$ are:
$4$, $8$, ... , $104$, $108$, $112$, $116$, $120$, ...
We can use the Divisibility Rule for $4$:
- A number is divisible by $4$ if the last two digits are divisible by $4$.
- Or, if the number can be divided by $2$ two times and the quotient is a whole number.
- $1516$ blueberry balls: The last two digits are $16$ and sure this is divisible by $4$. So $1516$ is divisible by $4$, too.
- $1035$ caramel cubes: Because the last digit is odd, this number can't be divided by $2$ and thus can't be divided by $4$.
- $1600$ strawberry strips: $00$ is divisible by $4$ because $0/4 = 0$ and thus $1600$ is divisible by $4$.
-
Find the correct statements for divisibility rules for 4, 5, 8, and 10.
HintsFor example: $35$ is divisible by $5$.
On the other hand $40$ is divisible by $5$, as well as by $10$.
$12$ is divisible by $4$, but you can't divide it by $8$.
- $20\div 2=6$
- $10\div 2=3$
SolutionDivisibility by $10$:
- Each number ending with $0$ is divisible by $10$.
- Each number ending with $5$ or $0$ is divisible by $5$.
- A number is divisible by $4$ if the last two digits are evenly divisible by $4$.
- ... or ... if the number is divisible by $2$ twice and the quotient is a whole number.
- A number is divisible by $8$ if the last three digits are evenly divisible by $8$.
- ... or ... if the number is divisible by $2$ three times and the quotient is a whole number.
-
Explain why the numbers are divisible using the rules for divisibility.
HintsKeep the rules beside in mind.
$110$ is divisible by $5$ and $748$ is divisible by $8$.
SolutionLet's practise those divisibility rules:
$110$ is divisible by $5$ and by $10$: ... by $10$ because it ends with $0$.
$748$ is divisible by $4$ and by $8$: ... by $4$ because the last two digits are evenly divisible by $4$. $48\div 4=12$.
$1656$ is divisible by $4$ and by $8$ as well: ... by $8$ because the last three digits are evenly divisible by $8$: $656\div 8=82$.
$1965$ is only divisible by $5$ because it ends with $5$.
Keep the following in mind:
- Each number divisible by $8$ is also divisible by $4$.
- Each number divisible by $10$ is also divisible by $5$.
-
Determine if the numbers are divisible by $4$ or $5$.
HintsA number is divisible by $4$ if the last two digits are divisible by $4$.
Or ... if the number is divisible by $2$ twice and the quotient is a whole number.
For example $116$ is divisible by $4$ but $114$ isn't.
Each number ending with $5$ or $0$ is divisible by $5$.
A number divisible by $4$ is at least even.
SolutionDivisibility by $4$ can be determined as follows:
- The last two digits are divisible by $4$.
- The number is divisible by $2$ twice and the quotient is a whole number.
- Only even numbers are divisible by $4$ but not all even numbers are divisible by $4$.
Let's have a look at $670$: Is this number also divisible by $4$? Let's check it by dividing by $2$ twice: $670\div 2=335$. The result, $335$, is odd and thus not evenly divisible by $2$. Therefore, $670$ isn't divisible by $4$.
Divisibility by $5$ can be determined as follows:
- The number ends with $5$ or $0$.
-
Calculate in which cases numbers are divisible by $2$.
HintsIf a number is divided by $2$ and doesn't have a remainder, it also means it's evenly divisible or divisible by $2$.
Write down the multiples of $2$.
The last digit of any number divisible by $2$ is $0$, $2$, $4$, $6$ or $8$.
SolutionThe multiples of $2$ are:
$2$, $4$, $6$, $8$, ..., $12$, $14$, $16$, ..., $102$, $104$, ...
- Each of those numbers is even.
- Or, in other words the last digit is divisible by $2$.
- Or, each number ends with $0$, $2$, $4$, $6$ or $8$.
-
Find the numbers that are divisible by $8$.
HintsA number is divisible by $8$ if the last three numbers are divisible by $8$.
... or ... if the number is divisible by $2$ three times and the quotient is a whole number.
Just look at the following:
$340$ is divisible by $4$ because $40$ is divisible by $4$ but it isn't divisible by $8$.
- $340\div 2=170$
- $170\div 2=85$
- The result is odd and thus not divisible by $2$.
A number divisible by $8$ is divisible is at the very least divisible by $4$.
SolutionA number is divisible by $8$ if the last three numbers are divisible by $8$.
Or if the number is divisible by $2$ three times and the quotient is a whole number.
- $1352$ is divisible by $8$ because $352\div 8=44$
- $1532$ isn't divisible by $8$, because $532=66.5$ and thus not a whole number.
- $2224\div 2=1112 \implies 1112\div 2=556 \implies 556\div 2=278$ this is a whole number. Thus $2224$ is divisible by $8$.
- $2220\div 2=1110 \implies 1110\div 2=555$. $555$ is an odd number and thus not evenly divisible by $2$. So we can't divide $2220$ by $2$ three times and get a whole number. $2220$ isn't divisible by $8$ (but is divisible by $4$).
- If you know that a three digit number is divisible by $8$ you can put as many digits in front as you want. So $72224$ is also divisible by $8$ because $2224$ is divisible by $8$.
- $2202$ can't be divisible by $8$ because $2202\div 2=1101$ results in an odd number.
- $22274\div 2=11137$ is also an odd number. So also isn't divisible by $8$.

Even and odd numbers

Divisibility Rules - 3, 6, 9

Divisibility Rules - 7

Divisibility Rules - 4, 5, 8, 10

Prime Numbers
Integers and their Opposites
Least Common Multiples
Prime Factorization
Adding and Subtracting Rational Numbers on a Number Line
Ordering Rational Numbers

Cube Roots

Rational and Irrational Numbers
Ordered Pairs on the Coordinate Plane

Finding the Greatest Common Factor
Adding and Subtracting Decimals
Comparing Fractions

Equivalent Fractions
Simplifying Fractions

Temperature Conversion

Decimal Expansions
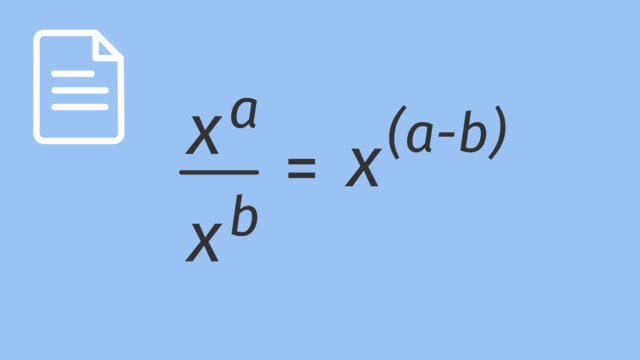
Division with Exponents
How to Convert Decimals Expansions
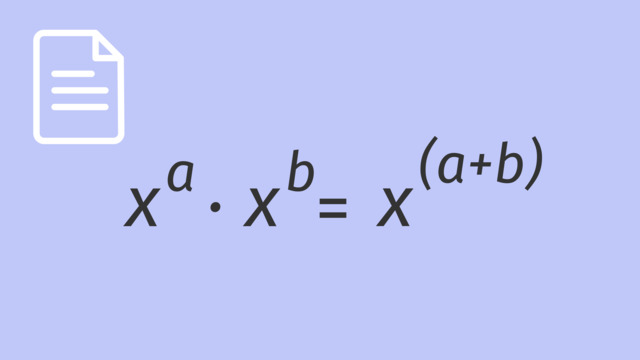
Multiplication with Exponents
Improper Fractions and Mixed Numbers

Multiplying Mixed Numbers: Word Problems











