Types of Numbers

Basics on the topic Types of Numbers
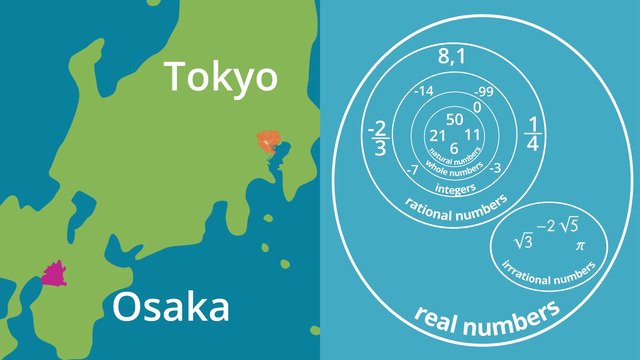
There are different types of numbers in the real number system. When you started to count things at a very early age, you learned the natural numbers. They are numbers such as 1, 2, 3, 4, 5, and so on. Then you discovered that there is a special number, zero. Natural numbers including zero are called whole numbers. Later, you learned about negative numbers such as -1, -2, -3, and so on. These numbers together with the whole numbers are united by the term 'integers.' Apart from integers there are also positive and negative fractions and decimals, either terminating or repeating. All fractions and decimals, together with integers, are rational numbers.
There are numbers that cannot be displayed as fractions, decimals, integers, and so on, such as many square roots, like √2, as well as special numbers like pi (π), or Euler's number (℮). These numbers are irrational numbers. Note that while natural numbers are integrated into whole numbers, whole numbers are integrated into integers, and integers are integrated into rational numbers. Rational numbers and irrational numbers are opposite number systems. Either a number belongs to the rational number system or to the irrational numbers. But: all numbers, rational and irrational, together, make up the real numbers.
This video will give you insight into the types of numbers with a great analogy that is easy to remember. It will also help you understand why all integers are rational numbers but not all rational numbers are integers.
Use properties of rational and irrational numbers. CCSS.MATH.CONTENT.HSN.RN.B.3
Transcript Types of Numbers
The system of different types of numbers is structured quite the same like the countries and cities all over the world. This is Hayato. He lives in Japan. This is a island nation in East Asia. The Japanese islands are in the Pacific.
To be more precise, we can say Hayato lives in Tokyo. To be even more precise, we can say Hayato lives in the district of Shibuya. There he lives on this street. Hayato lives exactly in this house. What has this to do with the real number system you ask? I will show you!
Whole Numbers
The first numbers that you learned were the natural numbers. These are numbers like 6, 11, 21, 50 and so on. It is like the different houses. All the natural numbers plus Zero belong to the whole numbers. Just like every house belongs to a street.
Integers
When we look what comes next, we find the integers. The integers are whole numbers as well as negative numbers. It is like all of the streets in the district of Shibuya.
Rational Numbers
One step further, there are the rational numbers. The rational numbers are positive and negative fractions as well as positive and negative decimals that terminate or repeat.
Note that not every rational number is an integer, but every integer is a rational number. It is like: Not everybody who lives in Tokyo also lives in Shibuya, but everybody who lives in the district Shibuya lives in Tokyo. There isn't just one city in Japan! You can see here is Osaka. Tokyo and Osaka are two separate cities. You cannot be in both places at the same time!
Irrational Numbers
A number can be a rational number or an irrational number like pi or the square root of 3. An irrational number cannot be written as a fraction or have a decimal that is repeating or terminating.
Real Numbers
Together the rational and the irrational numbers are in the real numbers. Just like Osaka and Tokyo are both in Japan.
You have seen the organization of our Number System is structured much like all of the countires and cities we live in. And also Hayato in Japan learns this. Because the Number system is the same all over the world.
Types of Numbers exercise
-
Explain the different types of numbers.
HintsObviously, every male Beagle is a Beagle. But on the other hand, all Beagles are not male Beagles.
Every Beagle is a dog. But, there also exist dogs like German Shepherds that aren't Beagles.
SolutionYou can see the system of different types of numbers in the picture on the right.
The numbers $6$, $21$, $11$ belong to a set called natural numbers. These numbers, along with $0$, give us the set of whole numbers. Negative numbers, $-1$, $-6$, $-23$ etc., together with numbers like $0$, $73$ and $75$ are called integers.
There are still other numbers like $\pm\frac14$ or $\pm0.375$, $\pm0.\overline{3}$, and can be rewritten in fraction form. These numbers, along with the integers combine to form the rational numbers.
Decimal numbers like $\pi$ and $e$, which are neither terminating nor repeating and cannot be written as fractions are called irrational numbers. These numbers, together with the rational numbers, make up all the real numbers.
-
Place each number in the smallest possible set.
HintsThe natural numbers are the numbers we use to count things.
The union of all the numbers is the set of real numbers.
Note that natural numbers, whole numbers, integers, and rational numbers are NOT irrational numbers.
An irrational number is a decimal number that does not terminate or repeat and cannot be written as a fraction.
Solution$6$ and $50$ are natural numbers. We use natural numbers to count things.
Whole numbers are natural numbers but also include $0$.
The set of negative numbers added to the set of whole numbers gives us the set of numbers called integers. For example, $-3$ and $-14$ are integers.
There are still other numbers like $\pm\frac35$ or $\pm0.5$, $\pm0.\overline{8}$ can all be rewritten in fraction form. These numbers along with the set of integers combine to form the rational numbers.
Decimal numbers like $\pi$, $e$ and $\sqrt3$, which do not terminate or repeat and cannot be written as fractions are called irrational numbers. These numbers, together with the rational numbers, make up the set of real numbers.
-
Identify which numbers don't belong to the given number type.
HintsWe use natural numbers to count and order things.
Integers are both natural numbers, zero, and negative whole numbers.
For example, $\frac13=0.\overline3$ is a rational number. It can be written as a fraction as well as a repeating decimal.
SolutionThe easiest way to remember the different number types is to remember examples of numbers belonging to each type.
With the exception of the irrational numbers, all the other number types are organized like Russian nesting dolls. For example:
- $314$ is a real number
- $314$ is a rational number
- $314$ is an integer
- $314$ is a whole number
- $314$ is a natural number
The note on the right side shows the correct solution. Here you find the mistakes already corrected:
- $-3$ is an integer but not a natural number
- $0$ is a whole number
- $3.14$ is a terminating decimal number and also a rational number, but it is not an integer
- $3.1\overline4$ is a repeating decimal number, so it's a rational number, and it is not an irrational number.
-
Assign each number to its correct number type.
Hints$\sqrt 2$ is an irrational number. Multiples of irrational numbers are also irrational, like $3\sqrt2$.
Natural numbers are used to count and order things.
Some examples are:
- $1$, $2$, $3$, ...
- $1\text{st}$, $2\text{nd}$, $3\text{rd}$, ...
The whole numbers are the natural numbers plus the number zero.
Integers are positive and negative whole numbers.
Some examples are:
- $... , -3, -2, -1, 0, 1, 2, 3, ...$
SolutionWe can write every number type as a set:
- natural numbers: $\{1, 2, 3, ...\}$,
- whole numbers: $\{0, 1, 2, 3, ...\}$,
- integers: $\{..., -3, -2, -1, 0, 1, 2, 3, ...\}$.
The representation of the rational numbers as a set isn't as easy as the number types shown above. So we'll define those numbers as follows:
- terminating or repeating decimal numbers such as $0.75$ and $0.\overline2$
- fractions such as $\pm\frac{435}{23}$
-
Analyze the statements about the different number types.
HintsNatural numbers are positive. So, if $a$ is a natural number, then $a>0$.
The number $0$, together with the natural numbers form the set of whole numbers.
$\frac13=0.\overline3$ is an example of a repeating decimal, and $7.5$ is an example of a rational number.
SolutionWe start with the natural numbers such as $11$, $21$. $-6$ is not a natural number.
The natural numbers, together with $0$, form the whole numbers. $-1$ is not a whole number.
Integers are numbers like $-3$ and $-99$. $-\frac23$ is not an integer.
The rational numbers are fractions such as $\frac14$ or decimals that terminate, like $8.1$, or repeat. $-2\sqrt 5$ is not a rational number.
Irrational numbers are not repeating decimals nor can they be written as fractions like $\pi$. $-\frac23$ is not an irrational number.
-
Decide to which number type the number belongs.
HintsThe real numbers include both rational and irrational numbers.
A number is either rational or irrational.
Every natural number is a whole number, but not vice versa.
Every whole number is a integer, but not vice versa.
Every integer is a rational number, but not vice versa.
Solution- Every natural number is also a whole number.
- Every whole number is also an integer.
- Every integer is also a rational number.
- Each number which is not rational is irrational.
- The rational and the irrational numbers together form the real numbers.
- $5.4$ is a rational number because it has a terminating decimal, and since all rational numbers are also real numbers, $5.4$ is also a real number. But $5.4$ is neither an integer nor a natural number.
- $\sqrt 5$ is an irrational number, and therefore not a rational number. However, $\sqrt 5$ is a real number.
- $\frac78$ is a fraction, and therefore it's a rational number.
- $-42$ is an integer, rational number, and real number. But $-42$ is not a whole number nor a natural number.

Variables

Simplifying Variable Expressions
Evaluating Expressions
How to do Order of Operations?

Distributive Property

Adding Integers

Subtracting Integers
Multiplying and Dividing Integers

Types of Numbers

Transforming Terminating Decimals to Fractions and Vice Versa

Transforming Simple Repeating Decimals to Fractions and Vice Versa
Rational Numbers on the Number Line
Standard and Scientific Notation
Using Operations with Scientific Notations












Hi :)
Hi
hi
Hi