Multiplying and Dividing Integers
- Multiplying and Dividing Integers
- Understanding the Rules of Multiplication and Division
- Multiplying Integers
- Dividing Integers

Basics on the topic Multiplying and Dividing Integers
Multiplying and Dividing Integers
In mathematics, multiplying and dividing integers involve working with both positive and negative numbers. These operations are essential in various real-life scenarios, such as accounting, temperature changes, and sports statistics.
Multiplying integers is the process of combining two or more integers to find their product. Dividing integers, on the other hand, is the process of splitting a quantity into equal parts.
Understanding the Rules of Multiplication and Division
To master multiplication and division with integers, it's crucial to know the basic rules. These rules tell us what happens when we multiply or divide positive and negative numbers. They're like guiding principles that help us figure out the results of math problems involving integers. Once we understand these rules, we can solve different kinds of problems more easily.
Multiplying Integers
| Rule | Outcome |
|---|---|
| Product of two positive integers | Positive |
| Product of two negative integers | Positive |
| Product of a positive and a negative integer | Negative |
Take a look at some examples:
- $3 \times 4 = 12$
- $(-2) \times (-5) = 10$
- $6 \times (-2) = -12$
- $(-3) \times 2 = -6$
- $8 \times 0 = 0$
Dividing Integers
| Rule | Outcome |
|---|---|
| Quotient of two positive integers | Positive |
| Quotient of two negative integers | Positive |
| Quotient of a positive integer and a negative integer | Negative |
Take a look at some examples:
- $12 \div 3 = 4$
- $(-10) \div (-2) = 5$
- $15 \div (-3) = -5$
- $\frac{-18}{3} = -6$
- $\frac{-24}{-4} = 6$
Multiplying and Dividing Integers – Practice
Practice applying these rules here!
Multiplying and Dividing Integers – Summary
Key Learnings from this Text:
- Understanding the rules of multiplying and dividing integers is crucial for solving mathematical problems involving positive and negative numbers.
- Multiplication results in a positive product when both integers have the same sign, while different signs yield a negative product.
- Division follows a similar pattern, with the quotient being positive for like signs and negative for unlike signs.
- Mastery of these rules enables efficient problem-solving in real-life applications such as accounting, temperature conversions, and sports statistics.
- Practice exercises provided in the text reinforce comprehension and application of these multiplication and division rules.
Once you have mastered the rules of multiplying and dividing integers, you can also learn the art of subtracting integers, and of course adding integers.
Multiplying and Dividing Integers – Frequently Asked Questions
Transcript Multiplying and Dividing Integers
So you think multiplying and dividing positive and negative integers is complicated... Don't stress! I'll show you how to make sense of this important math topic. Let's start with multiplication.
Multiplying positive Integers
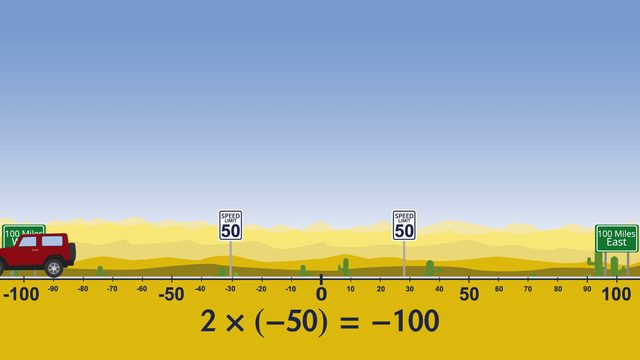
Imagine that you stand at a highway intersection. Cars are going east and west. Instead of a compass you can also use a number line, where east is the positive direction and west is the negative direction.
A blue car starts at your standing point, driving east, in a positive direction on the number line, going fifty miles per hour. After one hour, the blue car is here, fifty miles east of where you stand. And after two hours, the car is 100 miles east, at positive 100 on the number line.
Let's write this as an equation. Going for two hours 50 miles per hour in the positive direction can be written as 2 · 50 = 100. What happens if a car travels in the opposite direction? Let's go back to where you stand.
Multiplying negative Integers
Imagine, now, that a red car is going west, in a negative direction on the number line. Two hours later, the red car is 100 miles west of where you stand, at negative 100. I'll write this as a number sentence. Remember, going west in this case means going 50 miles per hour in negative direction. So we have 2 · −50 = −100.
Now, let's think about this topic another way. Where was a car going east two hours before it passed you standing at the intersection? Two hours before, driving east at fifty miles per hours, this car was one hundred miles west of where you stand, at minus 100 on the number line.
Let's write this as an equation. Two hours ago can be written as negative two. Remember, going east at fifty miles per hour means going in positive direction. So the equation is: −2 · 50 = −100.
And what about a car traveling west? Where was it two hours before? Traveling at fifty miles per hour in a negative direction on the number line, it was 100 miles east of where you stand. This is equal to positive 100.
I'll show you the equation. Negative two, which represents 2 hours ago, times negative fifty - for going 50 miles west, in the negative direction - is equal to positive one hundred: −2 · −50 = 100.
Rule for Multiplication and Division
Here's a cheat sheet of our equations. This equation is for going east in positive direction for two hours: two times fifty equals one hundred. This one shows going west in negative direction for two hours: 2 · −50 = −100. Here we look at where the car going east in positive direction was 2 hours ago: −2 · 50 = −100. And this shows where the car going west in negative direction was 2 hours ago: −2 · −50 = 100.
Can you find a pattern? You see here:
- If you multiply two positive numbers, you get a positive product
- If you multiply a postive with a negative you get a negative answer and
- If you multiply a negative with a positive, you also get a negative
- But if you multiply two negatives, you will get a positive product
Lets rearrange the equations. So now you have a rule: Multiplying like signs will give you a positive product and multiplying unlike signs will give a negative answer.
You know what's so great about this rule? It works the same for multiplying and dividing numbers! And, not just integers but fractions, too.
Hooray! With this simple rule, you can be the master of multiplying and dividing positive and negative numbers! But remember, you should never mess with the Space Time Continuum.
Multiplying and Dividing Integers exercise
-
Determine the correct distance and direction of the blue car by multiplying integers.
HintsThink about in which direction the car is traveling.
The distance the car travels can be expressed by: $distance = rate\times time$.
SolutionLet's see what information we have.
- The car is traveling at a constant $50$ miles per hour.
- The car drives for one hour.
- $50\times1$
- $50\times1 = 50$
-
Explain how multiplying integers gives you the distance and direction of each car.
HintsA positive number times a negative number results in a negative number.
A negative number times a negative number results in a positive number.
If we turn back time, it is equivalent to "negative" time.
SolutionLet's look at our word problems again.
- When our car travels at $50$ miles per hour for $2$ hours in a positive direction, we can write $50\times2$. Therefore, since we have two positive numbers, the car will travel $100$ miles in the positive direction which corresponds to an easterly direction.
- However, if our car is traveling in the negative direction at $50$ miles an hour for $2$ hours, we should write $(-50)\times2$. Now we are multiplying one positive number and one negative number. A positive number times a negative number always results in a negative product. In this case the car traveled $-100$ miles which means we travelled $100$ miles west.
- For "negative" time, we have to write the hours as a negative number. We can rewrite the third sentence mathematically as $50\times(-2)$. As you saw before, a positive number times a negative number always results in a negative product. So the car traveled $-100$ miles which is $100$ miles in an easterly direction.
- When the car drives $50$ miles per hour for $2$ hours in a negative direction, and then we turn back time $2$ hours, we should write this mathematically as $(-50)\times(-2)$. Remember, if we are multiplying like signs, the product is positive. Therefore, the car will travel $100$ miles in the positive direction which means it is traveling east.
-
Calculate the correct distance and direction using multiplication.
HintsRemember to multiply the car's speed by how many hours it is driven. Don't forget the signs!
SolutionIn this example, the car is always driving the speed limit ($65$ miles per hour).
- The car drives for $3$ hours in an easterly direction. We can write this sentence mathematically as $65\times3 = 195$.
- The car drives west for $2$ hours. Since west is our negative direction it makes $(-65)\times2 = -130$ miles.
- The car drives in a westerly direction for $4$ hours. Remember, west is our negative direction! We calculate $(-65)\times4 = -260$.
- The car drives east for $5$ hours. We have to evaluate $65\times5 = 325$,
-
Calculate the amount of money you have after going to the movies with your friends.
HintsThe money you receive is positive money, while money you spend is negative money.
Remember, you need two digits after the decimal!
SolutionWe can write $2\times\$20$ for the money you receive from your parents, $\$20$ from your mom and $\$20$ from your dad.
And we can write $(-1)\times((\$8\times3) + (\$5) + (\$1.50\times3))$ to express the amount of money you spent on movie tickets, popcorn and drinks, respectively. So our final expression would be:
- $2\times\$20 + (-1)\times(\$8\times3 + \$5 + \$1.50\times3)$
- $2\times\$20 + (-1)\times(\$24 + \$5) + \$4.50)$
- $2\times\$20 + (-1)\times\$24 + (-1)\times\$5 + (-1)\times\$4.50$
- $(\$40) + (-\$24) + (-\$5) + (-\$4.50)$
- $\$40 - \$24 - \$5 - \$4.50$
$\begin{array}{rcl} \$40 - \$24 - \$5 - \$4.50 & = & \$16 - \$5 - \$4.50\\ & = & \$11 - \$4.50\\ & = & \$ 6.50 \end{array}$
After treating your friends to movies and snacks you have $\$6.50$ left.
-
Determine the correct sign for the product of the pairs of signs below.
HintsSee if you can find a pattern:
- $5 \times 1 = 5$
- $5 \times 0 = 0$
- $(-5) \times (-1) = (5)$
- $5 \times (-2) = (-10)$
SolutionYou should have no problem remembering that a positive times a positive yields a positive answer.
- $(+) \times (+) = (+)$
- $(-) \times (+) = (-)$
- $(+) \times (-) = (-)$
- $(-) \times (-) = (+)$
-
Evaluate each of the expressions using multiplication and division.
HintsThe rule for signs when dividing two numbers is the same as for multiplication.
Zero is less than positive numbers and greater than negative numbers.
Solution- A positive number times another positive number equals a positive number: $(+)\times(+) = (+)$. As an example we have $5\times3 = 15$.
- A negative number times another negative number equals a positive number, too: $(-)\times(-) = (+)$. Thus we have $(-3)\times(-4) = 12$.
- Any number, positive or negative, times zero equals zero: $(+/-)\times(0) = (0)$. That leaves us with $10\times0 = 0$.
- The rules for signs when dividing numbers are the same as the rules when multiplying. Additionally, the location of the positive and negative numbers does not matter: $\frac{+}{-} = (-)$ or $\frac{-}{+} = (-)$. So $\frac{35}{-7} = -5$ equals $\frac{-35}{7} = -5$.
- A negative number times a positive number equals a negative number: $(-)\times(+) = (-)$. As an example we have $(-4)\times4 = -16$.
$\begin{array}{rcl} -4 \times 4 & = & -16 \\ \frac{35}{-7} & = & -~~5\\ 10 \times 0 & = & ~~~~~0\\ -3 \times -4 & = & ~~~12\\ 5 \times 3 & = & ~~~15 \end{array}$

Variables

Simplifying Variable Expressions
Evaluating Expressions
How to do Order of Operations?

Distributive Property

Adding Integers

Subtracting Integers

Multiplying and Dividing Integers
Types of Numbers

Transforming Terminating Decimals to Fractions and Vice Versa

Transforming Simple Repeating Decimals to Fractions and Vice Versa
Rational Numbers on the Number Line
Standard and Scientific Notation
Using Operations with Scientific Notations












this video gave me a quick refresher on how to mutiply intergers and can help me pass a test