Using Operations with Scientific Notations
- Operations with Scientific Notation
- Understanding Operations with Scientific Notation
- Multiplying Numbers in Scientific Notation – Steps
- Dividing Numbers in Scientific Notation – Steps
- Adjusting the Solution to Scientific Notation
Learning text on the topic Using Operations with Scientific Notations
Operations with Scientific Notation
In this text, we're going to explore how to perform operations like multiplication and division with numbers expressed in scientific notation. This skill is essential for handling very large or small numbers efficiently in math and science. We'll also touch on how to convert numbers to scientific notation, providing a comprehensive understanding of this useful mathematical tool.
For a refresher on the scientific notation rules, check out this video: Reading and Writing Scientific Notation
Understanding Operations with Scientific Notation
Scientific Notation is a way of expressing numbers that are very large or very small. It's expressed as a product of a number between 1 and 10 and a power of ten and can look like this: $4.3 \times 10^2$.
In the following section, you will learn the steps to finding the product or quotient of numbers in scientific notation.
Multiplying Numbers in Scientific Notation – Steps
- Multiply the decimal parts.
- Add the exponents of 10.
Dividing Numbers in Scientific Notation – Steps
- Divide the decimal parts.
- Subtract the exponent of the divisor from the exponent of the dividend.
Let’s check your understanding so far.
Adjusting the Solution to Scientific Notation
Don’t forget, according to the scientific notation definition, the decimal part should be greater than or equal to 1 and less than 10. Adjusting the decimal and the exponent accordingly will ensure your result is in the correct form of scientific notation.
| Condition | Action | Example Before Adjustment | Example After Adjustment |
|---|---|---|---|
| Decimal is greater than or equal to 10 | Shift decimal left; Increase exponent | $10 × 10^5$ | $1.0 × 10^6$ |
| Decimal is less than 1 | Shift decimal right; Decrease exponent | $0.4 × 10^3 $ | $4.0 × 10^2$ |
Let’s check your understanding so far:
Operations with Scientific Notation – Guided Practice
Let’s walk through some examples of multiplying and dividing numbers in scientific notation:
Operations with Scientific Notation – Real-World Application
Now that you have learned how to multiply and divide numbers written in scientific notation, let’s try to complete a few real-world problems.
Operations with Scientific Notation – Summary
Key Points from This Text:
- Scientific notation simplifies the process of working with very large or small numbers.
- Multiplication involves multiplying the decimal parts and adding the exponents.
- Division includes dividing the decimal parts and subtracting the exponents.
- Converting to and from scientific notation is an essential skill in these operations.
Explore more topics and practice problems on our website, including interactive exercises, videos, and worksheets to further enhance your understanding of scientific notation and other math concepts!
If you are looking for information on adding numbers in scientific notation or subtracting numbers in scientific notation, this video is a great resource: Adding and Subtracting Numbers in Scientific Notation
Operations with Scientific Notation – Frequently Asked Questions
Using Operations with Scientific Notations exercise
-
Calculate the standard form multiplication.
HintsTo make it easier rearrange it.
$2\times4$ and $10^{3}\times10^{5}$
When multiplying indices with the same base we add the powers.
$2\times4 = 8$
$8\times(10^{3}\times10^{5})$
Finish by putting your answer in standard form.
Solution$8\times10^{8}$
- Multiply $2$ and $4$ together
- Add the powers $3$ and $5$ = $10^{8}$
-
Calculate the standard form division
HintsTo make it easier rearrange it.
$9\div3$ and $10^{7}\div10^{5}$
When dividing indices with the same base we subtract the powers.
$9\div3 = 3$
$3\times(10^{7}\div10^{5})$
Finish by putting your answer in standard form.
Solution$3\times10^{2}$
- Divide $9$ by $3$
- Subtract the powers $7$ and $5$ = $10^{2}$
-
Find the product of two values in standard form
HintsTo make it easier rearrange it.
$4\times6$ and $10^{8}\times10^{4}$
When multiplying indices with the same base we ADD the powers.
$4\times6 = 24$
$24\times(10^{8}\times10^{4}) = 24\times10^{12}$ (We add the powers here)
The answer is not in standard form.
For this $24$ needs to be a number between $1$ and $10$ but this means we have to add one more to the indices.
Solution$2.4\times10^{13}$ in standard form.
-
Calculate and leave the answer in standard form.
HintsSome of the answers will need putting into standard form when the calculation has been done.
For example, if the answer is $27\times10^{3}$, we need to write it as a number between $1$ and $10$ and make adjustments.
$2.7\times10^{4}$
If the answer is already a number between $1$ and $10$ then no adjustment is necessary it is in standard form.
Solution- $(45\times10^{6})\div(3\times10^{2}) = 1.5\times10^{5}$
- $(7\times10^{3})\times(6\times10^{2}) = 4.2\times10^{6}$
- $(6\times10^{4})\times(7\times10^{2}) = 4.2\times10^{7}$
- $(42\times10^{8})\div(6\times10^{2}) = 7\times10^{6}$
-
Multiplying and dividing by powers of ten.
HintsWhen multiplying indices we add the powers if the base is the same.
When dividing indices we subtract the powers if the base is the same.
Solution- $10^{6}\times10^{2} = 10^{8}$
- $10^{3}\times10^{4} = 10^{7}$
- $10^{8}\div10^{2} = 10^{6}$
- $10^{5}\div10^{2} = 10^{3}$
When dividing indices we subtract the powers if the base is the same.
-
Divide the standard form numbers.
HintsThe operation we use for this problem is division.
Distance from London to Sydney $\div$ Distance from London to Paris
Distance from London to Sydney $\div$ Distance from London to Paris
$(1.05\times10^{4})\div(2.9\times10^{2})$
When we have divided $(1.05\times10^{4})\div(2.9\times10^{2})$ we need to make an adjustment to get the answer to the nearest whole number.
SolutionAnswer is $36$

Variables

Simplifying Variable Expressions
Evaluating Expressions
How to do Order of Operations?

Distributive Property

Adding Integers

Subtracting Integers
Multiplying and Dividing Integers
Types of Numbers

Transforming Terminating Decimals to Fractions and Vice Versa

Transforming Simple Repeating Decimals to Fractions and Vice Versa
Rational Numbers on the Number Line
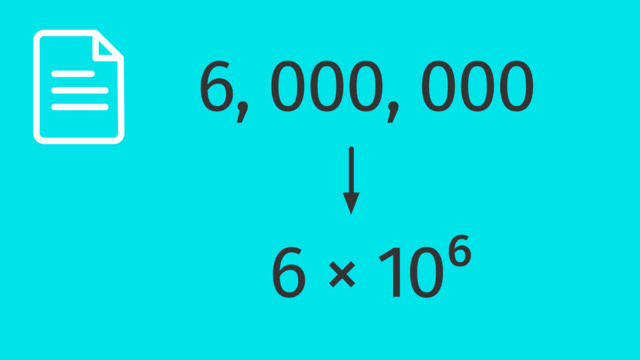
Standard and Scientific Notation
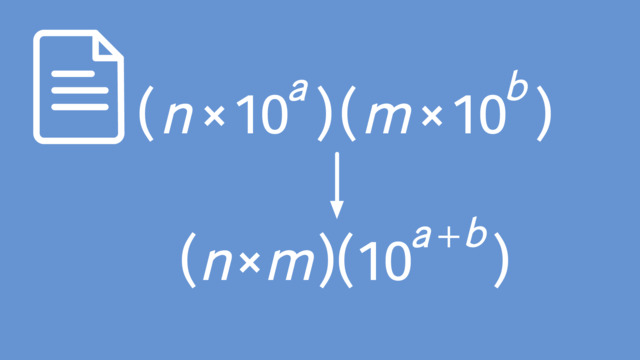
Using Operations with Scientific Notations










