Transforming Terminating Decimals to Fractions and Vice Versa
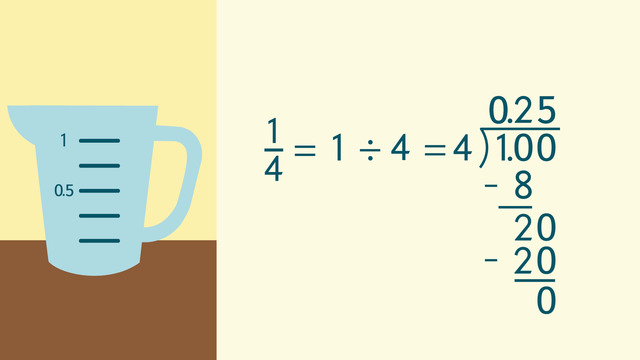

Basics on the topic Transforming Terminating Decimals to Fractions and Vice Versa
In real life it's often necessary to transform fractions into decimals or the other way round. Have you ever wondered why $0.25 is called a 'quarter?' Maybe you also came across a recipe where some measurements were given in fractions while others appeared in decimals.
When writing rational numbers as fractions or decimals, you can use two strategies, depending if you want to transform decimals into fractions or fractions into decimals.
Fractions are like unsolved division problems. Instead of ⅛, you can also write 1÷8, which you can solve in long division. Since your solution will be less than 1, write 0 above the division bar, include the decimal point, then add as many zeros to the dividend as you might need. Then start dividing as you're used to. Many simple fractions can be turned into decimals in only a few steps. Whenever you have 0 as a remainder, you are finished. Decimals that have only a few digits after the decimal point are called terminating decimals. There are fractions, such as ⅓, or 1÷3, however, that will never have 0 as a remainder and will go on forever with repeating digits. These are called repeating decimals.
For transforming terminating decimals into fractions you look at the length of your decimal repectively, to which place after the decimal point it goes to. 0.75, for example, goes to the hundreths place, so you can rewrite this number as 75 over 100. Guess how a decimal that goes to the thousandths place will be transformed into a fraction? Right, by rewriting this number with all digits after the decimal point over 1000.
Through the use of an everyday situation, this video will provide you with all you need to know about transforming fractions into terminating decimals and vice versa, including how to use long division for solutions that are less than 1.
Apply and extend previous understandings of operations with fractions. CCSS.MATH.CONTENT.7.NS.A.1
Transcript Transforming Terminating Decimals to Fractions and Vice Versa
Jim wants to make some muffins for his friend's birthday. What this has to do with writing rationals as fractions and terminating decimals, I will show you. He is searching the internet for a good recipe. Finally, he finds some really yummy looking muffins! Many of the ingredients are written as decimals of cup measurements.
Writing fractions as decimals
But when he looks at the measuring cup, all of the measurements are given in fractions! We can help Jim transform those fractions into decimals. Let's start with one half. Fractions are just unsolved division problems. One half is the same as saying 1 divided by 2.
To solve this by hand you must write the fraction as a long division problem.
- How many times does 2 go into 1? That's hard to say. We know that our answer is going to be a decimal that is less than 1, so let's add a decimal above the division bar and rewrite 1 as 1.0.
- Now we can ignore the decimals for a bit. Instead of thinking about how many times 2 goes into 1 we can think about how many times 2 goes into 10? 2 times 5 is 10.
- So you can write the 5 after the decimal above and subtract 10 just regular long division. 10 minus 10 is zero. The zero remainder tells us that we have finished the problem.1 divided by 2 is .5 or 0.5.
Let's try the same strategy with one fourth. One fourth is the same as 1 divided by 4 which can be rewritten as a long division problem.
- Because 4 also doesn't go into 1 you should add a decimal place and a zero after the one as well as a 0 and a decimal above the division bar. 4 goes into 10 2 times. Put the 2 after the decimal.
- Since 2 times 4 is 8 you should subtract 8 from 10 to get 2. 4 doesn't go into 2 so bring down a zero.
- 4 goes into 20 exactly 5 times. Subtract 20 from 20 to get 0 remaining so you have finished the problem! 1 divided by 4 is 0.25.
Writing decimals as fractions
Of course you can also transform decimals into fractions. Let's try 0.75 for example. 0.75 can also be called 75 hundreths because the decimal goes out to the hundreths place.
- 75 hundreths can be written as a fraction with 75 in the numerator and 100 in the denominator because we would also call this fraction 75 hundreths.
- Now, we can simplify the fraction because both numbers are divisible by 25. 75 divided by 25 is 3 and 100 divided by 25 is 4.
- The end result is three-fourths. This tells you 0.75 is three-fourths in fraction form.
Let's look at another example. 0.125. One is in the tens place, two is in the hundreths place, and the decimal ends in the thousandths place. This decimal is called one-hundred and twenty five thousandths. This tells you to write the fraction with 125 in the numerator and 1000 in the denominator.
We can simplify the fraction by dividing the top and bottom by 125. 125 divided by 125 is 1 and 1000 divided by 125 is 8. So 0.125 is 1/8 in fraction form.
After converting the measurements, Jim makes some delicious looking muffins. Not being able to resist the smell, he tries one. Yuck! The muffin tastes disgusting! He accidentally added salt instead of sugar. Poor Jim.
Transforming Terminating Decimals to Fractions and Vice Versa exercise
-
Write the decimals of the recipe as fractions.
HintsSimplify fractions by first determining the largest number that divides into the numerator and the denominator evenly.
SolutionJim's measuring cup gives all of the measurements in fractions. But many of the ingredients in his recipe are written as decimals of cup measurements.
So Jim has to convert all the decimals in the recipe into fractions.
Example:
The decimal $0.75$ goes out to the hundredths place. We can read this as $75$ hundredths. In a fraction, $75$ is the numerator and $100$ is the denominator.
$ 0.75 = \frac{75}{100}$
Now the fraction can be simplified. Therefore, Jim has to determine the Greatest Common Factor of the numbers. That is, the largest number that divides both the numerator and the denominator evenly. The Greatest Common Factor of $75$ and $100$ is $25$. So Jim has to divide $75$ and $100$ by $25$.
$ \frac{75}{100} = \frac{3}{4}$
As you can see, $0.75$ is $\frac{3}{4}$ in fraction form.
-
Find the correct decimals for each fraction.
HintsLong division ends when $0$ is our remainder, or if we get a repeating number (or sequence of numbers). If we didn't stop, we'd be dividing FOREVER! (i.e. $\frac13 = 0.33333333...$)
SolutionBaking sometimes demands converting fractions into decimals or vice versa. Jim's recipe is written in decimals of cup measurements, but his cup just has fractions. What can he do?
Fortunately, Jim knows that a fraction is just an unsolved division problem. That means that he can treat the fraction $\frac12$ as if he were dividing 2 into 1: $\frac12 = 1 \div 2$. After executing the long division, that leaves him with $1 \div 2 = 0.5$.
The second measurement he has to convert is $\frac14$. For getting a decimal he just follows the same steps including the long division. $ 1 \div4 $ equals the decimal $0.25$.
-
Convert each fraction into a decimal.
HintsWhen transforming a fraction into a decimal, you divide the nominator by the denominator.
SolutionYou can transform fractions into decimals. Fractions are just unsolved division problems which can be calculated by long division. Let's take a look at the following fractions.
- $\frac18 = 1 \div 8 = 0.125$
- $\frac38 = 3 \times \frac18 = 3 \times 0.125 = 0.375$
- $\frac34= 3 \div 4 = 0.75$
- $\frac78 = 7 \times \frac18 =7 \times 0.125 = 0.875$
- $\frac9{10} = 9 \div 10 = 0.9$
-
Identify where Sue succeeded in converting decimals into fractions.
HintsYou can convert a decimal to a fraction by putting the digits behind the decimal point in the nominator of the fraction. The number of digits behind the decimal point indicates the number of zeros behind the $1$ in the denominator.
The decimal $0.7$ has one digit behind the decimal point. So the fraction is $\frac7{10}$.
SolutionIt's no surprise this cake tastes disgusting. Let's take a look at the mistakes Sue made as well as the right conversions converting decimals into fractions.
- $0.6$ cups of flour is $\frac35$ths of a cup. That's right. You can calculate it like this: $0.6 = \frac{6}{10}= \frac{6\div2}{10\div2} = \frac35$.
- $0.45$ cups of butter were required. Let's convert it into fraction form: $0.45=\frac{45}{100} = \frac{45\div5}{100\div5} = \frac{9}{20}$. So Sue should have used $\frac9{20}$ cups of butter instead of $\frac{6}{20}$.
- $0.225$ cups of sugar are indicated in the recipe. What is the right fraction? $0.225 = \frac{225}{1000} = \frac{225\div25}{1000\div25} \div = \frac9{40}$. Sue has put $\frac{27}{40}$ cups of sugar into the cake. That is three times more sugar than requested.
- $0.3$ cups of apple sauce are $\frac3{10}$.
Now everything is totally clear and Jim and Sue know why their cake was a little too sugary and dry. Oh well, if at first you don't succeed...try again!
-
Decide if the given numbers are fractions or decimals.
HintsA fraction always has a nominator and a denominator.
A decimal can have a thousandths place, a fraction cannot.
Looking for decimals? Look for the decimal point.
SolutionKnowing different ways to represent numbers is important, too. You can often write a decimal as a fraction, and vice versa. Decimals look like this: $0.125$, $0.25$, $0.5$, $1.5$.
We can transform them in fractions, which look like this: $\frac18$, $\frac14$.
-
Find the numbers that represent the same value.
HintsYou can divide integers using long division.
SolutionTransforming fractions in decimals you can take a fraktion as a unsolved division. You simply divide the nominator by the denominator. Let's do this for all the fractions:
- $\frac1{25} = 1 \div 25 = 0.04$
- $\frac{12}{15} = 12 \div 15 = \frac45 = 0.8$
- $\frac68 = 6 \div 8 = \frac34 = 0.75$
- $\frac25 = 2 \div 5 = 0.4$

Variables

Simplifying Variable Expressions
Evaluating Expressions
How to do Order of Operations?

Distributive Property

Adding Integers

Subtracting Integers
Multiplying and Dividing Integers
Types of Numbers
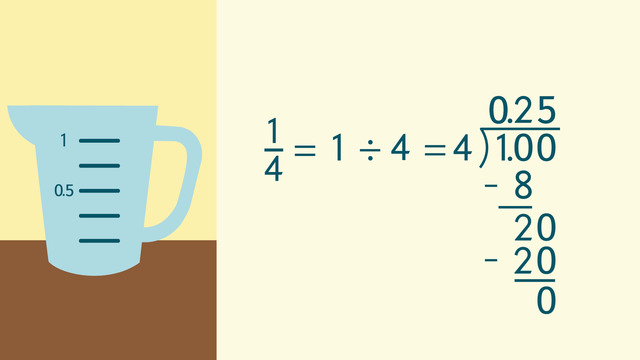
Transforming Terminating Decimals to Fractions and Vice Versa

Transforming Simple Repeating Decimals to Fractions and Vice Versa
Rational Numbers on the Number Line
Standard and Scientific Notation
Using Operations with Scientific Notations












Hi again! As always, thank you for your comments. To which video might you be referring? We do have another video in this topic called Transforming Simple Repeating Decimals to Fractions and Vice Versa. The content is very similar, but the aforementioned deals with repeating decimals instead of those that terminate.
This is a cool video, but I feel like I already saw another video like this... Um.
@spearson: Thank you so much for your kind comment. At the moment we are working on a new structure for our content so that the grade levels and the US Common Core Standards are much more transparent for teachers, students and parents. Best wishes!
This is a great way to present this concept but I think that adding what grade level this lesson targeted toward ( referencing the US Common Core Standards) might be of great help to teachers who are interested in using your product.