Rational Numbers on the Number Line

Basics on the topic Rational Numbers on the Number Line
Rational Numbers on a Number Line – Introduction
Working with rational numbers on a number line is a fundamental concept in mathematics. It enhances numerical fluency and paves the way for understanding more advanced math topics. Rational numbers include whole numbers, fractions, and decimals, and they can be positioned on a number line that extends infinitely in both directions.
Understanding Rational Numbers – Definition
A rational number is any number that can be written as a fraction, which means it is the quotient of two integers. The word rational comes from ratio, reflecting that these numbers represent a ratio of two quantities.
Rational numbers on a number line represent points that correspond to both whole numbers and fractions or decimals. A number line is a visual representation where these numbers are placed according to their value.
To get started, consider a number line as a horizontal line with evenly spaced divisions, each representing a unit or a fraction of a unit.
Rational Numbers on a Number Line – Example
| Step | Description | Illustration Request |
|---|---|---|
| 1 | Identify the numerator and denominator: The fraction $\frac{4}{5}$ has a numerator of 4 and a denominator of 5. The denominator tells us into how many equal parts the interval from 0 to 1 is divided. | An illustration showing a number line from 0 to 1, highlighting the concept of dividing the line based on the denominator. |
| 2 | Divide the number line: Imagine dividing the line into 5 equal sections between 0 and 1. | A detailed illustration of a number line from 0 to 1 divided into 5 equal parts, each part labeled. |
| 3 | Locate the number: Count four sections from 0. Here is where you'll place the dot for $\frac{4}{5}$. | An illustration of a number line with a dot marking the position of $\frac{4}{5}$, showing four parts from 0 highlighted or colored differently. |
Rational Numbers on a Number Line – Guided Practice
Let's practice placing a rational number on a number line.
Rational Numbers on a Number Line – Summary
Key Learnings from this Text:
Rational numbers include whole numbers, fractions, and decimals.
A number line is a tool that helps visualize and understand the position and magnitude of these numbers.
Placing a fraction on a number line involves dividing the interval into equal parts based on the denominator and locating the numeral based on the numerator.
Comparing and ordering rational numbers is easier with a number line, as their relative positions instantly indicate their size.
Operations like addition and subtraction of rational numbers can be visualized as movements along the number line.
Equivalent fractions occupy the same position on a number line, reinforcing the concept of equality among different representations.
Explore other content on our platform, such as interactive practice problems and videos, to deepen your understanding of rational numbers and their placement on a number line!
Rational Numbers on a Number Line – Frequently Asked Questions
Transcript Rational Numbers on the Number Line
Tim is feeling nervous. He is about to jump off the high dive at the local swimming pool. There he goes! How far above the water is he shortly after jumping?
Rational Numbers on the Number Line
To answer this question, we can look at the rational numbers on the number line. Let's see. The platform is 33 feet high. The tower is like a vertical number line. The surface of the water can be represented by 0, above we have positive numbers. Below the water we have the negative numbers.
Let's rotate the number line to a horizontal position to have a more precise look at how high Tim is above the water. As you can see at a first glance, Tim is somewhere between 20 and 30 feet above the water, or between 20 and 30 feet on the number line.
Fractions on the Number Line
To more accurately determine his location, we can zoom in to display a more detailed scale. Now you can see he is somewhere between 27 and 28 feet on the number line. Let's zoom in even more.
We can divide feet in to inches. As you know, there are 12 inches in 1 foot. So if you count from left to right on the number line, you land at 27 feet and 3 inches. This represents Tim's current location above the water.
In math, we often look at the number line without units. Instead of using inch notation, we can write our position on the number line as a fraction, with a value over twelve, because we divide one whole into 12 pieces. Here we are at 27 and 3 over twelve on the number line.
You can simplify this mixed number to 27 and 1 over 4, or 27 and one fourth. As you can see, our location on the number line between 27 and 28 remains the same. We have just changed the scale.
Decimals on the Number Line
We can represent 27 and one over four in yet another way, with a different scale: It can also be represented as a decimal: 27.25. If we display decimals on the number line, we divide our units into 10, 100 and so on. Here our number is exactly between 27.2 and 27.3. We can either zoom in more and divide tenths into hundreths, or we can assume the value is 27.25.
Negative Numbers on the Number Line
Let's get back to Tim. As he dives into the water, he is below 0 on the number line, where we have the negative numbers. We can use the negative numbers to represent how far Tim dived below the surface of the water. He dived somewhere between 0 and minus ten feet.
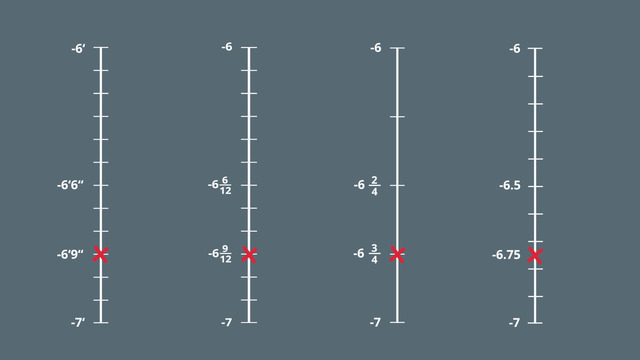
Let's take a closer look to figure out his exact depth. Now you can see, he dived somewhere between 6 and 7 feet below the surface, or between -6 and -7 feet on our number line. To be more accurate, let's zoom in even more.
We can divide feet into inches again. Now we count downwards, from -6 to -7. So Tim dived to -6 feet and 9 inches. Remember, you can also write this as a fraction: -6 and 9 over 12 feet, or simplified: -6 and 3 over 4. You can also write this mixed number as a decimal, which is: -6.75 feet.
Tim is happy that he overcame his fear. But wait, something is not right.
Rational Numbers on the Number Line exercise
-
Explain how far Tim is above the water shortly after jumping.
Hints$27'3''$ means $27$ feet and $3$ inches.
Decimals are divided in tenths and hundredths.
SolutionThe position of Tim shortly after jumping can be represented by a vertical number line. The surface of the water is our zero point. Above the water, we have the positive numbers. Below the water, we have the negative numbers.
Tim's height right after jumping is $27'3''$ which means $27$ feet and $3$ inches. Because there are $12$ inches in one foot, we can express his position on the number line. It is $27\frac3{12}$, which can be simplified to $27 \frac14$.
Alternatively his height can be transformed into decimal form: $27\frac14 = 27.25$.
-
Determine the decimals and fractions which equal the given values.
HintsThere are $12$ inches in $1$ foot.
You can simplify fractions by finding the Greatest Common Factor of the numerator and denominator. Then, you divide both numbers by the Greatest Common Factor.
Fractions can be transformed in decimals by dividing the numerator by the denominator.
SolutionAs you can see, there are several numbers that describe the same value. Feet can be converted to inches: There are $12$ inches in $1$ foot. So now we can express $6''$ as $\dfrac{6}{12}$. If we want, we can simplify it by converting it to a decimal, too.
-
Find the height of each jump in feet and inches.
HintsYou can convert a decimal into a fraction, too.
If we display decimals on the number line, we divide our units into tenths, hundredths and so on.
Therefore, $5.75$ can be interpreted as $5 \frac{75}{100}$, which is a fraction that can be simplified.
SolutionTommy, Richard, Lisa and Harry are jumping off the different diving boards at their local swimming pool. The height of the diving boards can be written as decimals on the number line as well as in feet and inches. Let's take a look:
Tommy: $22.25$ ft.
- $22.25$ ft. can be written as a fraction because decimals are divided in tenths and hundredths. So we have $22 \frac{25}{100}$ ft. Because the Greatest Common Factor of $25$ and $100$ is $25$, we can simplify the fraction to $\frac{1}{4}$. $22 \frac{1}{4} \text{ft.}$. Since one foot consists of $12$ inches, $22 \frac{1}{4} \text{ft.} = 22 \frac{3}{12}$ ft. So $22.25$ ft. is the same as $22' 3''$.
- $0.75$ ft. is $\frac{3}{4}$ ft. Multiplying the numerator and denominator by $3$ makes the denominator $12$, the number of inches in a foot. The number of inches is in the numerator, making our final conversion $19.75\text{ft.} = 19'9''$.
- $0.5$ ft. is $\frac{1}{2}$ ft. Multiplying the numerator and denominator by $6$ makes the denominator $12$, the number of inches in a foot. The number of inches is in the numerator, making our final conversion $15.5\text{ft.} = 15'6''$.
- Again, $0.5$ ft. is $\frac{1}{2}$ ft. Multiplying the numerator and denominator by $6$ makes the denominator $12$, the number of inches in a foot. The number of inches is in the numerator, making our final conversion $12.5\text{ft.} = 12'6''$.
-
Convert the depths to see which diver dove deepest.
HintsConvert the depths to the same unit of measure in order to compare more easily.
Every depth can be written as a fraction as well as in feet and inches.
SolutionWe want to find out who dove the deepest. Therefore, we have to compare the different values. It is a good idea to convert all the depths so they're expressed in the same units. In the table you can see all conversions. We have ordered the list beginning with the smallest depth to the greatest.
- $6.25$ ft.
- $6 \frac4{12}$ ft.
- $6'5''$
- $6 \frac12 $ ft.
-
Identify the steps for converting height from fraction to decimal form.
HintsThere are $12$ in $1$ foot.
So in fraction form, $10$ inches is $\frac{10}{12}$ of one foot.
The Greatest Common Factor of $10$ and $12$ is $2$. So we can simplify the fraction to $\frac{10\div2}{12\div2} = \frac{5}{6}$.
SolutionA distance given in feet and inches can be transformed into a decimal by following these simple steps:
- We have to determine the distance in feet and inches.
- We know that inches are smaller divisions of a foot. There are $12$ inches in one foot.
- This can be represented as a fraction. We put the inches in the numerator and the total number of inches in a foot, $12$, in the denominator.
- Finally, we divide the numerator by the denominator, getting the decimal.
-
Find out which distances Marshall ran this week.
HintsYou can convert every single value given into a fraction or decimal, showing the distance in miles. Alternatively, you can express miles in feet.
One helpful conversion you should keep in mind is: $\frac{1}{4}$ mile is $1320$ ft.
SolutionMarshall seems to be a really good runner. Let's take a look at the distances he covered this week. To compare the distances Marshall ran, we should convert all the numbers we have been given into one form. Let's begin with his shortest distance.
Remember, when converting units:
- $\text{feet} \times \dfrac{\text{miles}}{\text{feet}} = \text{miles}$
$\dfrac{37488\text{ ft.}}{5280\text{ ft.}} = 7.1 \text{ mi.}$
$~$
2. The next distance is $7.2$ miles, which is equal to:
$\begin{array}{rcl} 7 \text{ mi.} + 0.2 \text{ mi.} &=&\\ 7 \text{ mi.} + \frac{2}{10} \text{ mi.} &=&\\ 7 \times 5280 \text{ ft.} + \frac{5280 \text{ ft.} \times 2}{10} &=&\\ 36,960 \text{ ft.} + 1,056 \text{ ft.} &=& 38,016 \text{ ft.} \end{array}$
$~$
3. The distance $7 \frac{10}{20}$ miles ($7.5$ miles in decimal form) can be converted to feet as follows:
$\begin{array}{rcl} 7 \text{ mi.} + \frac{10}{20} \text{ mi.} &=&\\ 7 \text{ mi.} + \frac12 \text{ mi.} &=&\\ 7 \times 5280 \text{ ft.} + \frac{5280 \text{ ft.}}{2} &=&\\ 36,960 \text{ ft.} + 2640 \text{ ft.} &=& 39600 \text{ ft.} \end{array}$
$~$
4. The distance $7 \frac{3}{5}$ miles can be transformed the same way:
$\begin{array}{rcl} 7 \text{ mi.}+ \frac{3}{5} \text{ mi.} &=&\\ 7 \times 5280 \text{ ft.} + \frac{5280 \text{ ft.} \times 3}{5} &=&\\ 36,960 \text{ ft.} + 3168 \text{ ft.} &=& 40128 \text{ ft.} \end{array}$
$~$
5. The last distance of $41712\text{ ft.}$ can be transformed into miles the following way:
$41712\text{ ft.} \div 5280 = 7.9 \text{ mi.}$
$~$
See? It's much easier to compare distances when they are all in the same unit of measurement. And it`s easier to label numbers on the number line when they are transformed into decimals or mixed fractions.

Variables

Simplifying Variable Expressions
Evaluating Expressions
How to do Order of Operations?

Distributive Property

Adding Integers

Subtracting Integers
Multiplying and Dividing Integers
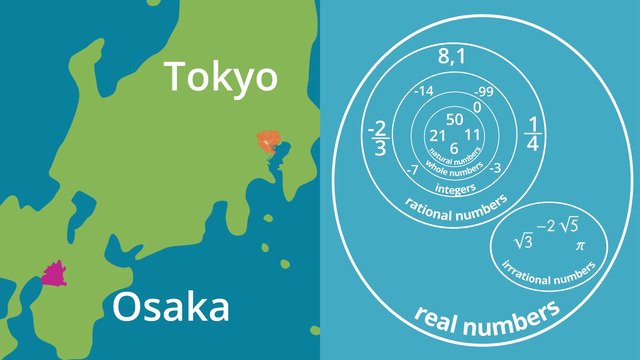
Types of Numbers

Transforming Terminating Decimals to Fractions and Vice Versa

Transforming Simple Repeating Decimals to Fractions and Vice Versa

Rational Numbers on the Number Line
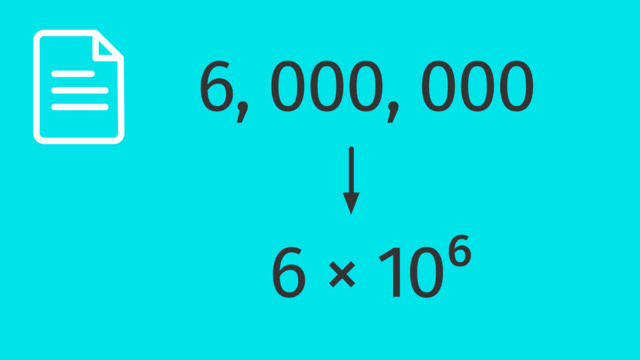
Standard and Scientific Notation
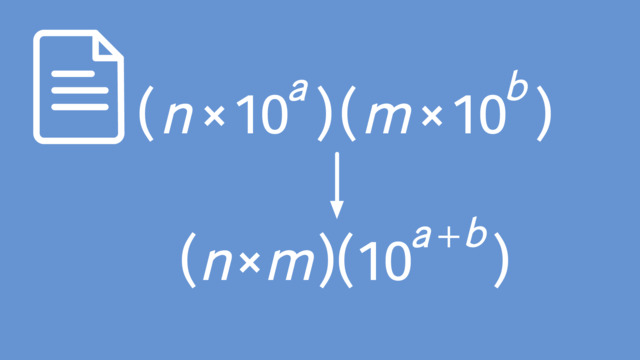
Using Operations with Scientific Notations









