How to do Order of Operations?

Basics on the topic How to do Order of Operations?
The order of operations (operator precedence) helps you with simplifying expressions or equations.
Maybe you wonder what you should do first: calculation inside the parantheses (brackets), or solving exponents (indices, powers, orders) and square roots (radicals)? And what about multiplication, division, addition, and subtraction? Do you multiply numbers first before you add? And in what order do you divide or subtract?
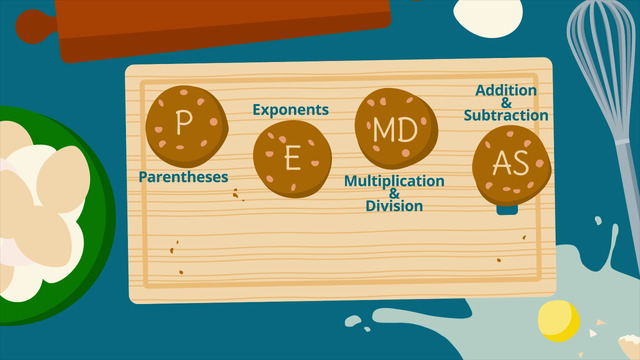
The order of operations gives you easy instructions of which operator has precendence if you have to handle expressions and equations. A mnemonic device for the order of operations is the acronym PEMDAS (BODMAS, BEDMAS, BIDMAS). To memorize it better you can make a sentence with those letters, such as "Please Excuse My Dear Aunt Sally."
In math, as well as in real-life situations, the order of operations is a necessary tool for all basic calculations and it is very easy to follow. You will need it for every following math topic, as well as in many science topics and in everyday life.
This video shows you situations that are common in daily life where order is relevant and shows you step by step how to transfer this knowledge into math. You will learn the precendence of operators in a funny, entertaining way, and will be guided through simplifying complex expressions the easy way. After watching this video, you will forever remember the right order of operations as you connect it with a great mnemonic device.
Write expressions in equivalent forms to solve problems. CCSS.MATH.CONTENT.HSA.SSE.B.3
Transcript How to do Order of Operations?
The Order of Operations. The ORDER of OPERATIONS! Yesterday, my dear Aunt Sally did everything in the wrong order. Look, she put her underpants above her skirt! She sent us to school. Then, she made our breakfast after we left. Later she baked cookies, but added the eggs in after the cookies came out.
My dear Aunt Sally did everything in the wrong order! As you can see, order is very important in everyday life. It is also important in math. Solving math problems is like following a recipe. You must follow the recipe for the Order of Operations, or PEMDAS to simplify expressions.
Steps in PEMDAS
- The first step in the Order of Operations is P for Parentheses. All expressions inside the parentheses should be evaluated first.
- E stands for Exponents. Exponents should be evaluated second.
- The next step is M and D, which stands for Multiplication and Division. After parentheses and exponents have been evaluated you should multiply and divide.
- Finally A and S means Addition and Subtraction. They represent the last step in the Order of Operations. The rule about solving left to right also applies to Addition and Subtraction.
Ok let’s evaluate some expressions. We’ll start with an easy one. You will see that following PEMDAS will always lead us to the right answer!
Calculation Example 1 & 2 using PEMDAS
First let’s look at two similar expressions: 8 - 2 + 5 and 8 – (2 + 5). The only difference between them is the use of parentheses. The first expression only has addition and subtraction so you should perform the operation in order from left to right: 8 − 2 = 6 and 6 + 5 = 11.
The second expression has parentheses. In PEMDAS the P for parentheses comes first. So, the Order of Operations tells you to evaluate the inside of the parentheses first: 2 + 5 = 7 and 8 − 7 = 1. Although these problems seem similar. They have two different answers.
Calculation Example 3 using PEMDAS
Okay, let's try a harder problem. This one has parentheses, exponents, addition, and subtraction! Parentheses come first. 8 − 2 gives you 6 and 5 + 2 gives you 7. Next comes Exponents: 6² = 36. Finally, you add 36 + 7 = 43.
Calculation Example 4 using PEMDAS
Now it's time to get even more tricky! Look at how many operations we are using! This expression has Parentheses, Exponents, Multiplication, Division, Addition, AND subtraction!
First you should be looking at the Parentheses. Inside you have 8 ÷ 2 − 2. Once inside the parentheses you have to use PEMDAS again. Division comes before subtraction so you must divide 8 by 2 before subtracting 2. Now you have 4 − 2. Resulting in 2. In the other parentheses you must evaluate the exponent before adding. You will need to square 5 before adding 2: 5² = 25, 25 + 2 will leave us with 27.
This problem is already looking better since we have taken care of the parentheses. The next step is E for exponents. 2 cubed gives you 8. Now we do multiplcation and division moving from left to right: 4 · 8 = 32 and 27 ÷ 9 = 3. The last step is Addition! 32 + 3 = 35. See? We started with this big expression, but by following the rules of PEMDAS we are able to simplify the expression to get 35!
PEMDAS Mnemonic
No matter how difficult the expression looks: Simply follow PEMDAS to get things done! You can remember PEMDAS with this sentence: Please excuse my dear Aunt Sally! So, please excuse my dear Aunt Sally. She was a little bit confused yesterday.
How to do Order of Operations? exercise
-
Using the correct order of operations, determine the right recipe.
HintsThe expressions $8 - 2 + 5$ and $8 - (2 + 5)$ seem similar. The only difference is the use of parentheses.
The first expression $8 - 2 + 5$ equals $11$. The second has the result $8 - (2 + 5) = 1$.
The last step is Addition & Subtraction. Always solve the equation from left to right.
SolutionAs you know, order is a very important matter in everyday life.
You might be wondering why we need an order of operations in math, too.
If the Order of Operations didn't exist, we wouldn't be sure which operation to do first...and this could have a large effect on the answer.
What kind of operations are covered in the Order of Operations?
- Parentheses
- Exponents
- Multiplication & Division
- Addition & Subtraction
By taking the first letter of each of our operations, we get PEMDAS - this way you will never forget the correct Order of Operations again!
-
Correctly simplify the expression $(8 - 2)^2 + (5 + 2)$.
HintsWhen you have simplified parentheses to a single number, you do not have to continue to write the parentheses.
Remember PEMDAS when evaluating the expressions.
Parentheses and Exponents come before Addition & Subtraction.
SolutionWe want to simplify the expression $(8 - 2)^2 + (5 + 2)$. At first, it's helpful to recognize which operations are included in our expression. We can see:
- two sets of parentheses
- one exponent
- addition (twice)
- and subtraction
- Parentheses
- Exponents
- Multiplication & Division
- Addition & Subtraction
Now, we can simplify the exponent: $6^2 + 7 = 36 + 7$. Finally, we add the remaining numbers, leaving us with $36 + 7 = 43$.
-
Correctly simplify the expression and help Timothy figure out Sarah's number.
HintsYou can evaluate this expression by following the rules of PEMDAS.
When evaluating Multiplication & Division or Addition & Subtraction you must evaluate the operations in the order they appear in the equation from left to right.
SolutionSarah had a cool idea. By encoding the last digits of her number, she has given Timothy a really difficult challenge.
But she didn't know that Timothy would be able to follow the rules of PEMDAS. He was able to simplify the expressions and find out the last three digits!
This is what he evaluated:
$\begin{array}{rcl} (2 \times 3)^2+1+800-(14-10)^2 & \overset{P}{=} & 6^2+1+800- 4^2\\ & \overset{E}{=} & 36 +1+800- 16\\ & \overset{A,S}{=} & 821 \end{array}$
Sarah's complete number is $1-713-555-1821$. Lucky Timothy.
-
Find out how many eggs and how much flour Sally needs for her cookie recipe.
HintsEvaluate Parentheses before Exponents.
When solving a problem, you can often simplify expressions by using PEMDAS.
Start with the Parentheses. Evaluate the Subtraction operators outside the parentheses in both expressions last.
You have to follow the rules of PEMDAS inside the parentheses, too.
SolutionWhat we have here is a really tasty recipe for cookies. But someone has substituted the amounts for eggs and flour with some longer mathematical expressions. We have to evaluate the expressions before we can go on baking. Let us take a look and see how many eggs we need:
$\begin{array}{rcl} (8-\frac{15}{5} \times 2)^3-\frac{(2+3)^2}{25} & \overset{D, A}{\longrightarrow} & (8-3 \times 2)^3-\frac{5^2}{25}\\ & \overset{M}{\longrightarrow} & (8-6)^3-\frac{5^2}{25}\\ & \overset{P}{\longrightarrow} & 2^3- \frac{5^2}{25}\\ & \overset{E}{\longrightarrow} & 8 - \frac{25}{25}\\ & \overset{D}{\longrightarrow} & 8 - 1\\ & \overset{S}{\longrightarrow} & 7 \end{array}$
We solve the parentheses first. Inside of the left parentheses, we have to simplify the fraction first. Then we multiply $3$ and $2$ and finally subtracted the two numbers. It's very important to follow the rules of PEMDAS inside parentheses, too.
After evaluating the parentheses, we should move on to the exponents. Now we can simplify the last fraction on the right side before subtracting in the end. That leaves us with $7$ eggs!
And how much flour do we need? Let's solve the last problem:
$\begin{array}{rcl} \frac{(6+2)^2}{4^2} \times 3 - \frac{(\frac42) ^3}{2^2} \times 3 & \overset{A,D}{\longrightarrow} & \frac{8^2}{4^2} \times 3 - \frac{2 ^3}{2^2} \times 3\\ & \overset{E}{\longrightarrow} & \frac{64}{16}\times 3 - \frac84 \times 3\\ & \overset{D}{\longrightarrow} & 4 \times 3 - 2 \times 3\\ & \overset{M}{\longrightarrow} & 12 - 6 \\ & \overset{S}{\longrightarrow} & 6 \end{array}$
For solving this expression, we solved the Parentheses first. Then we can evaluate the Exponents followed by Multiplication and Division. Finally, we subtracted from left to right. We found out that we need $6$ cups of flour.
Thanks to PEMDAS, we can now start baking!!!
-
Identify the mnemonic used to remember PEMDAS.
HintsLook at the initials of the words.
Which letters are in the acronym PEMDAS?
SolutionWith PEMDAS you can simplify expressions: you simply have to follow the rules.
First evaluate Parentheses, then Exponents, followed by Multiplication and Division and finally you evaluate Addition and Subtraction.
Remember to always evaluate Multiplication and Division as well as Addition and Subtraction from left to right!
You can remember this order with a funny mnemonic:
Please Excuse My Dear Aunt Sally.
-
Simplify the expressions by using the order of operations.
HintsFollow the rules of PEMDAS.
PEMDAS stands for:
- Parentheses
- Exponents
- Multiplication & Division
- Addition & Subtraction
Sometimes there are Parentheses inside Parentheses. In this case, solve the inner Parentheses first.
The inside of Parentheses are no different -- follow the rules of PEMDAS.
SolutionBy following the rules of PEMDAS you cannot fail solving expressions the right way. Let us take a closer look at the following expression. Here we can see Parentheses inside Parentheses.
$\begin{array}{rcl} 75 - 2 \times \left( 3 + \frac{\left(3+24 \right)}{9} \right)^2 & \overset{P,P,A}{\longrightarrow} & 75 - 2 \times \left( 3 + \frac{27}{9} \right)^2\\ & \overset{P,D}{\longrightarrow} & 75 - 2 \times \left( 3+3 \right)^2\\ & \overset{P,A}{\longrightarrow} & 75 - 2 \times 6^2\\ & \overset{E}{\longrightarrow} & 75 - 2 \times 36\\ & \overset{M}{\longrightarrow} & 75 - 72\\ & \overset{S}{\longrightarrow} & 3 \end{array}$
We should first look at the expression as a whole. We see that there's another set of Parentheses inside the Parentheses. To solve the outer Parentheses, we must first evaluate the inner Parentheses. Finally, we can solve the outer Parentheses and proceeded as usual, following the rules of PEMDAS.

Variables

Simplifying Variable Expressions
Evaluating Expressions

How to do Order of Operations?

Distributive Property

Adding Integers

Subtracting Integers
Multiplying and Dividing Integers
Types of Numbers

Transforming Terminating Decimals to Fractions and Vice Versa

Transforming Simple Repeating Decimals to Fractions and Vice Versa
Rational Numbers on the Number Line
Standard and Scientific Notation
Using Operations with Scientific Notations












lolllll
For free no cap
:)