Evaluating Expressions
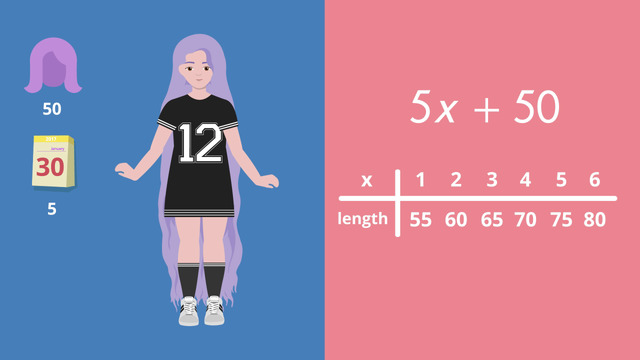

Basics on the topic Evaluating Expressions
To evaluate expressions, it is helpful to review some words associated with this topic. First, what is an expression, and how does it differ from an equation?
An expression does not have an equal sign while an equation does. An equation includes two expressions with an equal sign in between the expressions. Expressions are made up of terms. A term can be a number by itself, and this is called a constant. A term can also include a variable which is a letter or other symbol that stands in for an unknown value, usually the letter x. Variables can be alone or attached to a numbers by the operation of multiplication or division such as 3x or x/3. This number attached to the variable is called a coefficient.
Now that you know the words to describe expressions, you are ready to simplify them. To simplify expressions, follow PEMDAS then combine the like terms. Constants go with constants, and same variables go with same variables. When you are ready to evaluate the expressions which means to solve them for a specific value of the variable, follow the correct order of operations, PEMDAS. To learn more about evaluating expressions and have a laugh, watch this video.
Write expressions in equivalent forms to solve problems. CCSS.MATH.CONTENT.HSA.SSE.B.3
Transcript Evaluating Expressions
Let me tell you a story about evaluating expressions…
Once upon a time
"Once upon a time, there lived a girl in a tower
She was there every day, hour after hour."
"Her name was Rap-Punzel,
a mischievious damsel,
whose hair was a handful"
"The love of her life, Prince MC,
was in love with Rap-Punzel... as in love as can be.
They waited for the day and waited for the time
when the prince could scale the tower with a short little climb."
"But he's tired of waiting, what a waste of days.
He should evaluate expressions but he doesn't know the way"
Let's help MC Prince. At the start of this tale, Rap-Punzel’s hair is 50 inches long. Each month, it grows 5 inches." Let’s write this as an expression… 50 is the constant number in this expression, meaning it does not change. We said before that her hair grows at a rate of 5 inches per month. The number of months is the unknown quantity, which we will call x. We can also use any other variable.
Expression for the length of Rap-Punzel's hair
The number five is the coefficient of the variable. So… the expression to describe the length of Rap-Punzel's hair after a variable number of months is 5x + 50. Ok, let's use our expression to evaluate the length of Rap-Punzel's glorious hair over a period of a few months. Let’s set up a function table… When evaluating expressions, always remember to use the correct order of operations.
Calculation of further growth
After 1 month, the length of her hair is equal to 5(1) + 50, for a total length of 55 inches. After 2 months, the length is 2(5) + 50, which equals 60. Let’s fill in the table... OMG, after 6 months, Rap-Punzel’s hair is a staggering 80 inches long! But, disaster struck and Rap-Punzel discovered that her glorious hair was not so glorious after all ... - it was full of split ends. (Pause). Impulsively, ....
... she cut her hair. Now it's just 10 inches long. To keep her hair healthy, Rap-Punzel must trim her hair two inches every month. Despondent, MC Prince wondered, how much longer must he wait to be with his beloved? Let's modify our expression. 5x for the growth per month minus 2x for the trimming per month plus ten for the starting length.
Insert the right numbers
Now, simplify the expression. 3x + 10. MC Prince wondered, '...after six more months, how long will her hair be?...' Evaluate the expression, this time, letting x equal six… use the correct order of operations, 3(6) = 18; plus ten it is equal to twenty-eight. Her hair will only be twenty-eight inches long!
"Still waiting outside, MC Prince began to doubt
without Rapunzel in his life, he's like a plant in a drought
he had an idea, on which he was keen"
what's this? OH NO...he bought magic beans...
Evaluating Expressions exercise
-
Calculate the length of hair after given number of months.
HintsYou can use a linear function to represent the length of Rap-Punzel's hair. The unknown quantity is the number of months.
Let's look at another example: The amount of money you receive on your birthday increases by $\$5$ each year. You start with $\$15$.
- After one year, you receive $\$15+\$5=\$20$
- After two years, you receive $\$20+\$5=\$25$
You have to multiply the number of months that have passed by the rate her hair grows, then add $50$.
SolutionIn the beginning, Rap-Punzel's hair is $50$ inches long. Because her hair grows $5$ inches per month, we know that Rap-Punzel's hair grows as follows:
- After one year: $50+5=55$ inches
- After two years: $55+5=60$ inches
- After three years: $60+5=65$ inches
- After four years: $65+5=70$ inches
- After five years: $70+5=75$ inches
- After six years: $75+5=80$ inches
$\begin{array}{c|c|c|c|c|c|c} x&1&2&3&4&5&6\\ \hline \text{length}&55&60&65&70&75&80 \end{array}$
-
Find an equation that represents Rap-Punzel's hair length after $x$ months.
HintsRap-Punzel's hair grows $5$ inches per month. He hair has grown:
- 10 inches after $2$ months
- 15 inches after $3$ months
To avoid split ends, Rap-Punzel has to trim her hair. This means she has to cut her hair. Is her hair getting longer or shorter?
You can simplify expressions and equations by combining like terms. For example: $2$ apples plus $3$ bananas plus $4$ apples results in $6$ apples and $3$ bananas.
SolutionPoor Rap-Punzel and poor Prince MC. Rap-Punzel's hair grows $5$ inches per month. But she has split ends. To avoid getting split ends, she has to cut her hair $2$ inches per month.
How can we write this as a mathematical expression?
- Let's represent the rate of growth: $5x$
- Next,write the expression to represent Rap-Punzel trimming her hair: $-2x$
- Finally, we add $10$
We can combine the like terms to get $3x+10$ as our final expression.
-
Evaluate how long Rap-Punzel's hair is after one year.
HintsFirst, determine the expression that represents the length of Rap-Punzel's hair after $x$ months. $x$ can be any number of months: $1$, $2$, $3$, ...
Rap-Punzel's starting hair length is the constant.
To write the simplified expression, the coefficient can be found by determining the difference between the growth rate of Rap-Punzel's hair minus the monthly trimming in order to avoid split ends.
SolutionFirst, let's write an expression representing the length of Rap-Punzel's hair after $x$ months:
- To start, Rap-Punzel's hair is $10$ inches long. This is our constant.
- The variable is the unknown quantity of months, which we'll call $x$.
- The coefficient can be found by calculating the net growth per month of Rap-Punzel's hair. In this case, her hair grows $5$ inches per month, but she cuts $2$ inches each month as well. So our coefficient becomes $5-2=3$.
To determine the length of Rap-Punzel's hair after one year, we can plug in $x=12$.
$\begin{array}{rcl} 3(12)+10&=&\\ 36+10&=&46 \end{array}$
So after one year, Rap-Punzel's hair is $46$ inches long.
The tower is a BIT taller than $46$ inches... Poor Prince MC.
-
Determine how long it takes until the magic beanstalk grows to a height of $100$ inches.
HintsThe expression is:
coefficient $\times x +$ constant.
To isolate the variable $x$, use opposite operations:
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
Check your solution by plugging in your value for $x$:
$0.5x + 20$
Did the expression simplify to $100$?
SolutionWaiting for Rap-Punzel's hair to grow takes too long and learning how to climb is too expensive, so Prince MC decides to buy some magic beans to grow a plant. The beanstalk has:
- an initial height of 20 inches - this is the constant
- a growth rate of 0.5 inches per day - this is the coefficient
- the variable $x$ to the unknown number of days
To figure out the number of days the beans need to reach $100$ inches, we must solve the equation for $x$:
$0.5x+20=100$
We use Opposite Operations to isolate $x$:
$\begin{array}{rclcl} 0.5x + 20y &=& 100 \\ \color{#669900}{-20} && \color{#669900}{-20} \\ 0.5x &=& 80 \\ \color{#669900}{\times 2} && \color{#669900}{\times 2} \\ x &=& 160 \end{array}$
So, after $160$ days, more than $5$ months, the magic beanstalk will be $100$ inches high.
Is this tall enough to reach Rap-Punzel?
-
Label the different parts of the expression.
HintsA constant is independent of the variable.
The term above represents the length of Rap-Punzel's hair after $x$ months.
In the beginning, Rap-Punzel's hair is $50$ inches long.
SolutionThis expression represents the length of Rap-Punzel's hair after $x$ months.
- The coefficient to the variable is the rate of growth, $5$.
- $x$ represents the unknown number of months.
- Finally, our constant is the starting length of her Rap-Punzel's hair in inches, $50$.
-
Decide which function table belongs to which equation.
HintsTo match to the correct function table, make sure more than $x$-$y$ pair satisfies the equation.
For each equation on the right, plug in several different $x$s and compare the answers.
SolutionA function table is a useful tool used to set up a linear equation.
This is what it looks like:
$\begin{array}{c|c|c|c} x& & & \\ \hline f(x)&&& \end{array}$
- You can plug in different values for the variable $x$ and check the corresponding $f(x)$.
- $f(x) = 3x + 4$
$\begin{array}{rcl} 3(3) + 4 &=& \\ 9 + 4 &=& 13 \end{array}$
So our function table should look like this:
$\begin{array}{c|c|c|c|c|c} x& 1&2 &3&4&5 \\ \hline f(x)&7&10&13&16&19 \end{array}$
$~$
- $f(x) = 4x + 3$
$~$
- $f(x) = 2x + 5$
$~$
- $f(x) = 5x + 2$

Variables

Simplifying Variable Expressions
Evaluating Expressions
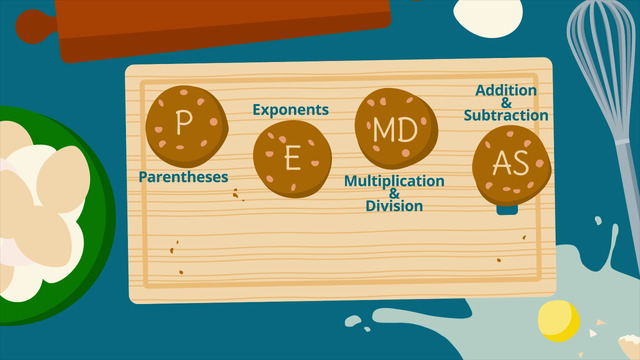
How to do Order of Operations?

Distributive Property

Adding Integers

Subtracting Integers
Multiplying and Dividing Integers
Types of Numbers

Transforming Terminating Decimals to Fractions and Vice Versa

Transforming Simple Repeating Decimals to Fractions and Vice Versa
Rational Numbers on the Number Line
Standard and Scientific Notation
Using Operations with Scientific Notations












Yeaaaah paaaaaad
if you need to get rid of the coefficient as in 0.5x it is best to divide. so divide both sides by 0.5 and that will give you the answer.