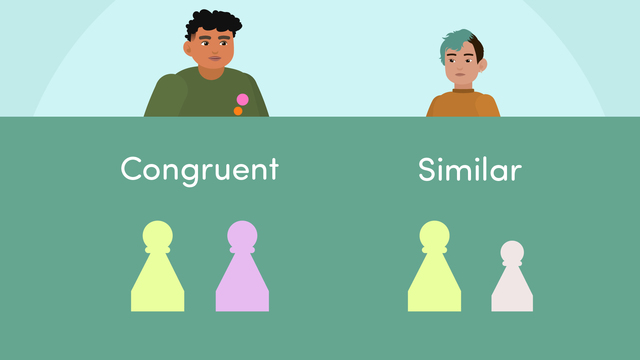
What are Congruence and Similarity?

Basics on the topic What are Congruence and Similarity?
Congruence in Geometry – Introduction
When we talk about congruence in geometry, we're discussing one of the foundational concepts in the subject. Just as we recognize twins for their identical features, we identify geometric shapes as congruent when they are exact duplicates of each other in size and shape.
Understanding Congruence – Definition
Congruence is a term used to describe two objects with the same shape and size. In geometry, two figures are said to be congruent if they can be perfectly overlapped through rigid motions like translations (slides), rotations (turns), and reflections (flips).
Rules for Congruence
- Corresponding angles must be equal.
- Corresponding sides must be equal in length.
- The figures must have the same shape and size, but their orientation or position may vary.
Similarity in Geometry – Definition
While congruence focuses on identical measurements, similarity in geometry looks at the proportionate resemblance between figures.
Two geometric figures are similar if their corresponding angles are equal and the lengths of their corresponding sides are proportional. This is akin to having a consistent shape but different sizes.
Rules for Similarity
- All corresponding angles are equal.
- The ratios of the lengths of corresponding sides are equal.
- The figures must have the same shape but not necessarily the same size.
Congruence vs. Similarity – Example
To illustrate the difference between congruence and similarity, consider two triangles:
- Triangle A and Triangle B have sides that are exactly the same length and angles that are identical. They are congruent.
- Triangle C and Triangle D have the same angle measurements as Triangle A, but their sides are twice as long. Triangle C and D are similar to Triangle A.
Congruence and Similarity – Guided Practice
Let's put it into practice. Given two rectangles, Rectangle X: 4 cm by 6 cm, and Rectangle Y: 8 cm by 12 cm, are these rectangles similar, congruent, or neither?
Congruence and Similarity – Application
Imagine you are designing a quilt with patterned squares. If you want the quilt to have a harmonious look, you will need to decide whether you want all squares to be congruent or similar in various sizes.
Congruence and Similarity – Summary
Key Learnings from this Text:
- Congruence and similarity are fundamental concepts in geometry, dealing with the equality and proportion of shapes.
- Congruent shapes are exact duplicates in size and shape, whereas similar shapes have the same shape but different sizes.
- Rigid motions like translation, rotation, and reflection can help determine congruence.
- The study of congruence and similarity is crucial in various fields, including art, architecture, and engineering.
| Aspect | Similar Figures | Congruent Figures |
|---|---|---|
| Corresponding Angles | All corresponding angles are equal. | All corresponding angles must be equal. |
| Corresponding Sides | The ratios of the lengths of corresponding sides are equal. | All corresponding sides must be equal in length. |
| Shape and Size Requirements | Must have the same shape, but not necessarily the same size. | Must have the exact same shape and size. |
| Orientation/Position | Can be different; orientation and position do not affect similarity. | Can be different; orientation and position may vary. |
Explore the world of geometry further by engaging with interactive practice problems, diving into detailed explanations, and applying these concepts in real-world scenarios!
Congruence and Similarity – Frequently Asked Questions
Transcript What are Congruence and Similarity?
Luis is planning a game night with his friend, Kai to play Shape Shift Quest. But, he realizes he is missing some pieces for the game and decides to give his new 3D printer a go at replacing them. In order to do that he needs to answer the question: 'What are congruence and similarity?' Congruent means that two figures are the exact same shape and size. They also have the same side lengths and angle measurements. Similar means that two figures are the same shape, but they are different sizes Similar figures do not have the same side lengths, but they do have the same angle measurements. Luis is ready to compare the first piece he printed. Are these two figures similar or congruent? They are the same shape, but because it is a different size, these pieces are similar. Luis adjusts some measurements and copies the game piece again. Are these two figures similar or congruent? Again, the game piece is the same shape, but because it is larger, it is similar. What type of changes does Luis need to make for the game piece to be congruent? Remember, to have a congruent figure, it needs to be the same shape and the same size. Are these two figures similar or congruent? He is successful! The game piece he created is the same shape and the same size, so it's congruent. Game night is approaching quickly, and Luis has one more missing triangular game piece to recreate. After it's done, he realizes that the piece has the same angle measurements, but the lengths are different. Pause the video here and determine if these triangles are similar or congruent and why. These triangles are similar because they have the same angle measurements, but different side lengths. A way to show that figures have the same angle measurements is to use matching 'arcs' on the angles. Here's Luis' next piece. Pause the video to determine whether these two figures are similar or congruent. These two shapes are similar again because they have the same angle size but the new game piece has shorter side lengths. Luis is running out of time and tries one last time to make the missing piece. How did he do? Pause the video here and decide, are these similar or congruent? They are the same! Since the corresponding angles are equal, as well as the side lengths, these two figures are congruent. Luis and Kai are ready for a match-up for board game night! Remember in order for two figures to be congruent, they must have the exact same angles and side lengths and are a copy of each other. If they are the same shape but have different sizes, they are similar. It looks like Luis is going to need to teach Kai all he knows about congruency versus similarity!
What are Congruence and Similarity? exercise
-
What is congruency?
HintsThe shapes shown are congruent. What do you notice about the side lengths and the angles?
The shapes shown are not congruent.
There are $2$ correct answers.
SolutionCongruent shapes are exactly the same shape and size.
- Corresponding angles are the same
- Corresponding side lengths are the same
-
Understand the definition of congruency.
HintsCongruent shapes have the same corresponding angles and the same corresponding side lengths.
If two shapes are not congruent they would not have the same size corresponding side lengths.
There are 2 correct answers.
SolutionThese pairs of shapes are not congruent.
They have the same corresponding angles but different sized corresponding side lengths.
-
Are the triangles similar?
HintsSimilar triangles have all equally sized corresponding angles, but the corresponding side lengths are different.
These shapes are similar.
SolutionSimilar triangles have:
- corresponding angles equal
- corresponding side lengths are different
-
Which one is not congruent?
HintsCongruent shapes have corresponding angles of exactly the same size.
The sum of angles in a triangle $= 180^\circ$.
To find a missing angle we can subtract the sum of the other two angles from $180^\circ$.
For example, missing angle $= 180 - 50 - 60 = 70^\circ$.
SolutionThis is the triangle which is not congruent.
Not all of the angles are the same. We are looking for $95^\circ$, $49^\circ$ and $36^\circ$.
Here we have:
- $36^\circ$ is correct
- $98^\circ$ is incorrect
- $180 - 36 - 98 = 46^\circ$, also incorrect.
-
Where is the congruent shape?
HintsTo be congruent, a shape must have the same size angles and corresponding side lengths.
The rectangles are congruent.
If a shape has the same size angles but not side lengths, it is similar.
The rectangles are similar.
There are $3$ correct answers here.
SolutionThese shapes are all congruent as they are exactly the same size.
-
Looking for similarity.
HintsWe are looking for a multiplier to make the sides proportional. For example,
To make the shape similar all the sides have to be proportional. Here is what happens when they are not. The shape does not look the same proportionally.
Solution- Rectangle $8\times4$ is similar to $2\times1$, that is $4$ times longer sides.
- Rectangle $12\times3$ is similar to $4\times1$, that is $3$ times longer sides.
- Rectangle $6\times4$ is similar to $3\times2$, that is $2$ times longer sides.
- Rectangle $15\times5$ is similar to $3\times1$, that is $5$ times longer sides.
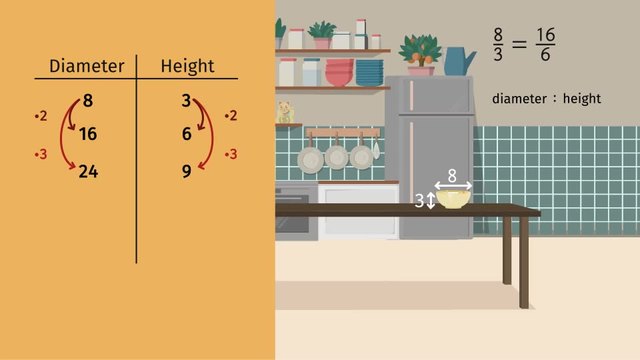
Determining Equivalent Ratios
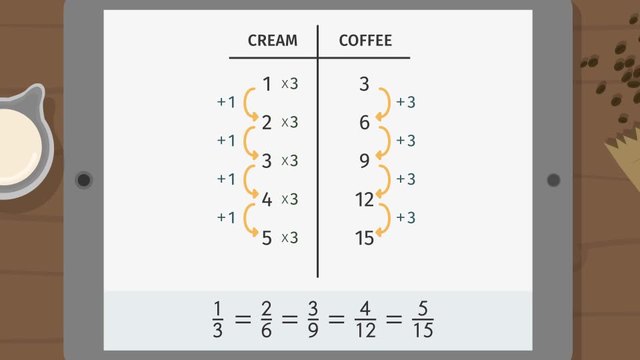
Ratio Tables - Additive and Multiplicative Structure

Comparing Ratios Using Ratio Tables
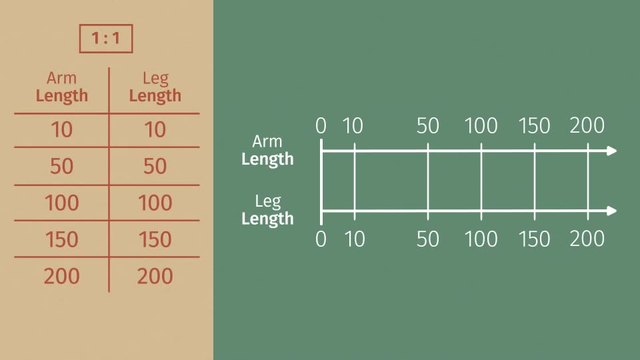
From Ratio Tables to Double Number Lines
From Ratio Tables to Equations

Plotting Ratios on the Coordinate Plane

Reviewing Representations of Ratios

What are Congruence and Similarity?









