From Ratio Tables to Equations

Basics on the topic From Ratio Tables to Equations
After this lesson, you will be able to transform ratio tables into equations.
The lesson begins by teaching you how to identify patterns in a ratio table and to determine the constant rate. It leads you to learn how to assign variables and set up the proportion to get the equation. It concludes with isolating the desired variable in the equation for ease of manipulation.
Learn about changing ratio tables to equations by understanding the balance of processes in the human body!
This video includes key concepts, notation, and vocabulary such as ratio (a relationship between two non-negative numbers, both of which are not zero); ratio table (a structured set of equivalent ratios); constant rate (the rate at which a quantity changes in relation to another is fixed or unchanging); proportion (two or more equivalent ratios); variable (a symbol, usually a letter, that is used to represent one or more values) and equation (a statement of equality between two quantities).
Before watching this video, you should already be familiar with ratio, ratio table, constant rate, variable, and equation.
After watching this video, you will be prepared to learn to solve real-world and mathematical problems involving unit rate, percent, and measurement conversion.
Common Core Standard(s) in focus: 6.RP.A.3 A video intended for math students in the 6th grade Recommended for students who are 11 - 12 years old
Transcript From Ratio Tables to Equations
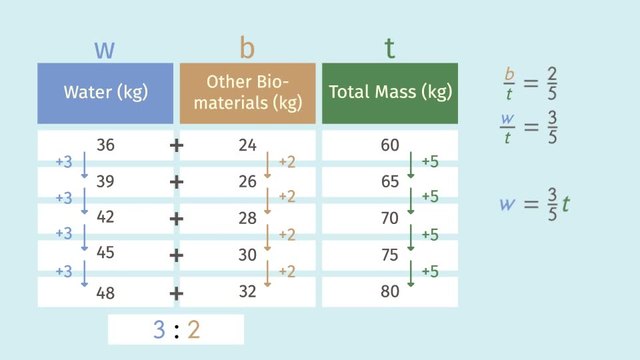
When you listen to your favorite song, the music can move you! While dancing the robot, you're running on the electric energy of quality beats! In fact, our bodies work like machines. There are moving parts, and lots of inputs and outputs. We eat, drink, and breathe to keep our bodies in balance. Changing ratio tables to equations, gives us a way to understand the balance of processes that happen in our bodies. Let's start by examining our breathing process. The air we breathe in and out is composed of many gases. These gases are mostly nitrogen, and some parts oxygen and carbon dioxide. The nitrogen is stable as it is and doesn't change within our bodies. On the other hand, the inhaled oxygen is used to perform many important functions, like fueling our muscles, while the carbon dioxide is exhaled as a waste gas. Let's think about the breath you just took. Only 60 milliliters of that air is oxygen. We can use "ml" to represent mililiters. 60 mililiters is about the volume of two ping pong balls. Now breath out. With that exhale, only 15 milliliters of that is carbon dioxide. That’s about half a ping pong ball. So, what is the ratio of oxygen inhaled to carbon dioxide exhaled? 60 to 15. Here we have a ratio table. Now it shows what happens when we start to dance faster and our breathing volume increases. Do you notice any patterns in the table? For every 4 milliliters of increase in oxygen inhaled, there is a corresponding 1 milliliter increase in carbon dioxide exhaled. The 4 to 1 ratio is preserved in every breath! From this ratio table we can write an equation that examines the relationship between oxygen and carbon dioxide. An equation gives us a tool to find any gas amounts we want. We can use the 4 to 1 pattern, ratio, we marked earlier to help us establish the relationship. We see that 60 equals the pattern of 4 times 15, 64 equals 4 times 16, and so on, and so forth. With this relationship identified, it is easier to write an equation. When writing an equation, we should should identify our variables. We want to know about the oxygen and carbon dioxide relationship for any amount. Therefore, let’s call oxygen, 'x', and carbon dioxide, 'c'. In general, we can see oxygen, 'x', equals 4 times the carbon dioxide, 'c'. That's a useful equation and will give us how much oxygen we inhaled when we know how much carbon dioxide was exhaled. If you want to solve for carbon dioxide you can use the same equation and just isolate the c variable. You can’t live on oxygen alone. To move with fluidity, you need water, too. Even though different people have different masses, they all have a similar water to other bio-material components. This table shows the mass of water to other bio-materials found in different guys in kilograms. Do you see any patterns in this table? As the water mass increases by 3, the other bio-materials mass increases by 2, maintaining a nice, hydrated, 3 to 2 ratio. This ratio could give us our water mass when we know the mass of our other biomaterials. Do you know the mass of your other bio-materials? However, most people only know their total mass. How can we calculate the total mass of the given information? Just add the water and other bio-materials together to get the total mass for each person. Notice anything interesting in the ratio table? Because the water increased by 3 each time and the bio-material increased by 2 combined they increased by 5. This constant increase can be nicely translated into equations using ratios. Remember to first identify your variables. Let's define water as 'w', other bio-materials as 'b,' and total mass as 't.' So, we can write the proportion of other bio-materials, 'b', to total, 't', as 2 to 5, and the proportion of water,'w', to total, 't' as 3 to 5. We can solve for whichever variable we want to dance with. For example, let's pick water, 'w'! Isolate 'w' by multiplying both sides by 't'. This gives us water is equal to three-fifths 't.' For example, if your total mass is 55 kilograms, 33 of those kilograms are from water. So, we've learned a lot. Can you summarize the steps needed to go from ratio tables to equations? First, identify patterns. There should always be a constant ratio. Second, identify your variables and set-up the equivalent ratios. Lastly, isolate the variable you want to find. Smooth dancers have to breathe deep, stay hydrated, and understand their bodies. Oh? Looks like we've overlooked some gases. His machine is also running on fumes. But, that's another story.
From Ratio Tables to Equations exercise
-
Decide which statements are true given the ratio.
HintsWhen ratios are written as words the order is important. The first word corresponds to the first number, the second word corresponds to the second number.
If you have a ratio of $7$ oranges to $6$ apples. That means for every $7$ oranges you have $6$ apples. So if you have $21$ oranges that means you have $18$ apples. The ratio $\frac { 21 }{ 18 } = \frac { 7 }{ 6 } $
SolutionWhen ratios are written as words, order is important! The first word corresponds to the first number and the second word corresponds to the second number.
In this problem, it is given that the ratio of milliliters of oxygen inhaled to carbon dioxide exhaled is 4 to 1. This means that the $4$ corresponds to oxygen and the $1$ corresponds to carbon dioxide. In order for a statement below to be true, this oxygen $4$ to carbon dioxide $1$ ratio needs to there.
- For every $4$ ml of oxygen inhaled, $1$ ml of carbon dioxide is exhaled is true. This statement holds the oxygen $4$ to carbon dioxide $1$ ratio given.
- For every $1$ ml of oxygen inhaled, $4$ ml of carbon dioxide is exhaled is not true. In this statement the ratio of oxygen to carbon dioxide is $1$ to $4$, not $4$ to $1$ from the given statement. The ratio is backwards in this answer.
- When $80$ ml of oxygen is inhaled, $20$ ml of carbon dioxide is exhaled is true. It is given that the ratio of oxygen to carbon dioxide is $4$ to $1$. In this statement, the ratio is $80$ to $20$. $80$ to $20$ can be simplified by dividing both numbers by $20$, resulting in $4$ to $1$.
- The amount of oxygen inhaled is $4$ times the amount of carbon dioxide exhaled is true. From the given statement we know that for every $4$ ml of oxygen inhaled, $1$ ml of carbon dioxide is exhaled. To test if this statement is true, multiply the amount of carbon dioxide exhaled ($1$) by $4$, which gives us $4$, which is the amount of oxygen inhaled in the example.
- If $40$ ml of carbon dioxide was exhaled, then $10$ ml of oxygen was inhaled is not true. From the given statement we know oxygen to carbon dioxide is $4$ to $1$. In this statement we are given carbon dioxide to oxygen is $40$ to $10$. We can simplify this ratio by dividing both numbers by $10$, which gives us a ratio of $4$ to $1$. This may seem correct, but in this statement we are given carbon dioxide first, not oxygen like the given statement. The numbers may be the same, but the order of the ratio is not, so this is not a true statement.
-
Writing equations given a ratio table
HintsIn equivalent ratios, the numerator of the first fraction is related to the numerator of the second fraction and the denominator of the first fraction is related to the denominator of the second fraction.
When solving for a variable, perform the opposite operation to move any other variable or constant to the other side of the equation. Remember that addition and subtraction are opposites, while multiplication and division are opposites.
If asked to solve $\frac { a } { d } = \frac { 5 } { 7 } $ for $a$ in terms of $d$, multiply both sides of the equation by $d$ to get $ a= \frac { 5 } { 7 } d$.
SolutionThe first step in writing an equation is always to define the variables. Once variables have been defined, then you can follow the following steps:
- Set up equivalent ratios. Remember that in equivalent ratios the numerators all must represent the same thing, and the denominators all must represent the same thing.
- To identify the equation that compares water to other bio-materials, look for the equation with both the variable that represents water, $w$, and the variable that represents other bio-materials, $b$. Also make sure that this equation has the correct ration of water to other bio-materials, which is $3$ to $2$. The equation is: $\frac{w}{b} =\frac{2}{3}$.
- When asked to isolate a variable, that means to solve for that variable and get everything else on the other side of the equations. In this step we must solve $\frac{w}{b} =\frac{2}{3}$ for $w$. To solve for $w$, we need to use the opposite operation to move the $b$ to the other side. The fraction $\frac { w }{ b }$ means $w$ divided by $b$, to move $b$ we must do the opposite of dividing, which is to multiply both sides by $b$.
- The resulting equation is $ w = \frac{3}{2} b $
-
Complete the ratio table and find an equation
HintsFind the constant increase in each column by looking for the pattern. What is being added as you go down each column?
Identify the ratio of femur length to body height for the table.
Look across each row. What is the relationship between femur length and body height?
SolutionWhen analyzing a table, it is a good idea to look for patterns in the table. You should notice that the Femur Length column is increasing by $1$ as the Body Height column is increasing by $4$. This gives us a Femur Length to Body Height Ratio of $1$ to $4$.
This ratio of $1$ to $4$ can also help find the relationship across each column. In this table, the Femur Length, $f$, multiplied by $4$ results in the Body Height, $h$.
It is a good idea to check to make sure this works for every row.
- $15\cdot 4=60$ ✓
- $16\cdot 4=64$ ✓
- $17\cdot 4=68$ ✓
- $18\cdot 4=72$ ✓
This equation can be used to find Body Height, $h$, given and Femur Length, $f$. In this question you were asked to determine the Body Height given a Femur Length of 30 inches. Using the equation created, $4f=h$, and given $f=30$, you will have $4(30)=h$, when simplified gives you $120 =h$.
Therefore when a Femur Length is $30$ inches, the Body Height is $120$ inches.
-
Match ratio table to equation
HintsIdentify the constant increase in each column.
Set up equivalent ratios, $\frac{x}{y}$ and solve for x.
Look for the relationship across each row. What operation do you have to perform on the value in $y$ to get the value in $x$?
SolutionOne way to write equations for ratio tables is to set up equivalent fractions. To write equivalent fractions you will need to find the constant increase for each variable by looking for the pattern down each column.
The constant increase, equivalent fractions, and equations for each table are listed below.
- The constant increase for $x$ is $1$. The constant increase for $y$ is $2$. The equivalent ratio equation is $\frac{x}{y} = \frac{1}{2}$. To solve for $x$, multiply both sides by $y$ to get the equation $x= \frac{1}{2}y$.
- The constant increase for $x$ is $2$. The constant increase for $y$ is $10$. The equivalent ratio equation is $\frac{x}{y} = \frac{2}{10}$. To solve for $x$, multiply both sides by $y$ to get the equation $x= \frac{2}{10}y$. The fraction $\frac{2}{10}$ can be simplified by dividing the numerator and denominator by 2 to get $\frac{1}{5}$. The final equation for table $2$ is $x= \frac{1}{5}y$ .
- The constant increase for $x$ is $5$. The constant increase for $y$ is $1$. The equivalent ratio equation is $\frac{x}{y} = \frac{5}{1}$. To solve for $x$, multiply both sides by $y$ to get the equation $x= \frac{5}{1}y$. The fraction $\frac{5}{1}$ simplifies to $5$, so the final equation for table $3$ is $x=5y$.
- The constant increase for $x$ is $12$. The constant increase for $y$ is $3$. The equivalent ratio equation is $\frac{x}{y} = \frac{12}{3}$. To solve for $x$, multiply both sides by $y$ to get the equation $x= \frac{12}{3}y$. The fraction $\frac{12}{3}$ simplifies to $4$, so the final equation for table $4$ is $x=4y$.
-
Identify patterns in ratio tables.
HintsTo find the ratio $x$ to $y$, you must first find the constant increase for each column.
To identify the constant increase, look for a pattern in either the $x$- or $y$- column. Look at one column at a time. Start from the first number and ask yourself "what number am I adding to get the number below?" Repeat this for the entire column, if this value is the same for each then it is the the constant increase for that column.
Look at the table below.
$\begin{array}{|c|c|} \hline x & y \\ \hline 1 & 5 \\ 2 & 10 \\ 3 & 15 \\ 4 & 20 \\ \hline \end{array}$
- Look at the numbers in the $x$-column: $1$, $2$, $3$, $4$.
- Ask yourself what number do can I add to $1$ to get to $2$? Repeat this for each number in the $x$-column:
- If you added the same number each time, then that is the constant increase for the $x$.
- Do the same for the $y$-column:
- The number you added every time should have been the same, this is the constant increase for $y$.
Look at the table below.
$\begin{array}{|c|c|} \hline x & y \\ \hline 1 & 5 \\ 2 & 10 \\ 3 & 15 \\ 4 & 20 \\ \hline \end{array}$
You can see that the $x$ increases by $1$ and the $y$ increases by $5$, this gives an $x$ to $y$ ratio of $1:5$.
SolutionFirst identify the constant increase in both the $x$ and $y$ column for each table. Then, set up your $x$ to $y$ ratio using the constant increases you found.
- For the first table, constant increase for $x$ is $4$ and for $y$ is $3$. The ratio $x$ to $y$ for this table is $4:3$.
- For the second table, the constant increase for $x$ is $1$ and for $y$ is $7$. The ratio $x$ to $y$ for this table is $1:7$.
- For the third table, the constant increase for $x$ is $3$ and for $y$ is $4$. The ratio $x$ to $y$ for this table is $3:4$.
- For the fourth table, the constant increase for $x$ is $7$ and for $y$ is $1$. The ratio $x$ to $y$ for this table is $7:1$.
-
Given an equation fill out the ratio tables
HintsTo find a missing value in a table, substitute in a number you are given into the equation and simplify.
To decide which ratio equation to use, look at the value you are given. Which equation can you substitute that value into and simplify without having to rearrange the formula?
Let's look at an example:
Given the two equations $a=\frac{3}{4}b$ and $b=\frac{4}{3}a$ , find $a$ if $b=8$.
I would choose the equation that has $a$ isolated and $b$ on the other side: $a=\frac{3}{4}b$ .
Then, substitute $b=8$ and simplify. $a=\frac{3}{4}(8)\\ a=\frac{24}{4} \\ a=6$
SolutionIn this problem, three equivalent equations are given. That means that you can use whichever equation makes the most sense based on whether you are given $d$ or $t$.
You may choose to use one equation to complete the table, or use all of them. There is not a rule as to which equation you have to use. Some equations may take less steps, but all of them will arrive at the same answer.
When solving this problem, I chose to use the equation with the variable isolated that I was not given. For example, if I was given $d$ and needed to find $t$, I would use the equation $t=\frac{7}{2}d$.
Let's start by substituting in all $d$-values given into $t=\frac{7}{2}d$.
- $d=2$, $t=\frac{7}{2}(2)$, $t=\frac{14}{2}$, so $t=7$.
- $d=6$, $t=\frac{7}{2}(6)$, $t=\frac{42}{2}$, so $t=21$
- $d=10$, $t=\frac{7}{2}(10)$, $t=\frac{70}{2}$, so $t=35$
- $t=14$, $d=\frac{2}{7}(14)$, $t=\frac {28}{7}$, so $t=4$
- $t=70$, $d=\frac{2}{7}(70)$, $t=\frac {140}{7}$, so $t=20$
Determining Equivalent Ratios
Ratio Tables - Additive and Multiplicative Structure

Comparing Ratios Using Ratio Tables
From Ratio Tables to Double Number Lines

From Ratio Tables to Equations

Plotting Ratios on the Coordinate Plane

Reviewing Representations of Ratios
What are Congruence and Similarity?











