From Ratio Tables to Double Number Lines

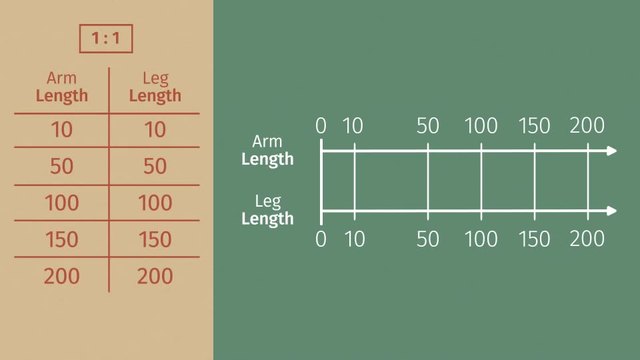
Dr. Frank N. Stein takes his daughter Mary to visit the Build-a-Monster shop for her birthday. At Build-a-Monster, she can build a friendly monster to join her at the playground! She can make her monster as wild as she is! At Build-a-Monster, kids first choose a torso from one of the cards. Mary selects a 75 centimeter dinosaur torso for her monster. Next, kids get to choose the ratio of arm to leg length. But these cards list the different choices in a ratio table! Mary has trouble visualizing the different ratios. We can help Mary visualize her different options by transforming ratio tables into double number lines! Let's take a look at one of Build-a-Monster's Arm-to-Leg Ratio cards. The first card shows a ratio of one-to-one, that means the arms and legs are literally the same length. We can visualize this in a ratio table and expand the lengths as desired. If we wanted to display this information as a double number line, we can start with a regular number line showing just the arm length. Since we already have the numbers for the arm length, we can simply rewrite them horizontally like this. Then, we can put tick marks for each of our data points. We can draw our second number line for the leg length, but we want the tick marks to be in the same place as in the first number line and write the corresponding numbers from our table below our existing tick marks. This double number line tells us that the arm length will be the same as the leg length. Mary chooses 200 cm to 200 cm. Oops! The legs look too long. Since Mary hopes to bring her monster to the park to play, Mary picks a different arm to leg ratio that'll help her monster swing around on the jungle gym better! She chooses an arm to leg ratio of 5 to 2. Let's look what happens when we draw a double number line for this ratio. Just like in the first ratio, we start with a number line with a tick mark for the desired arm length. Like with all double number lines, we want to extend our tick marks to the second number line as well. This time, in our second number line, our first tick mark will now start at 2, so every time we cover 5 units on the first number line, we only cover 2 units on the second. We've recorded arm lengths on the top number line, and the corresponding leg lengths on the bottom. The bigger the numbers get, the further along the number line they go. What about an arm length of 80 centimeters? With a double number line that’s easy to visualize. Let's resize our double number line so that our tick marks for arm length are in increments of 10. Don't worry. We haven't changed the ratio! It's still 5 to 2! Now we just need to fill in the numbers on our number line. The top of the number line is easy, we just count by 10s. The bottom of the number line is a bit different. Here, we have to count by 4s. A double number line makes it easy to compare ratios visually and choose an arm to leg ratio. Mary likes the ratio 5 to 2, so she chooses the equivalent ratio of 60 to 24. This will make Mary’s monster a perfect jungle gym buddy! Now let's move on to hands and feet, the Build-a-Monster specialty! Mary chooses a hand to foot ratio of 3 to 7! But this card only has a few options. We can fill in the blanks by calculating a few equivalent ratios. Starting with our original ratio, every time we add 3 cm to the hand length, we must add 7 cm to the foot length. For our first blank, adding 3 to 3 gives us 6, and adding 7 to 7 gives us 14. Now we've found an equivalent ratio to the ratio 3 to 7. We can fill in the rest of the blanks in a similar way, checking periodically to make sure we get the equivalent ratios given on the cards. Mary wants her monster to have hands at least 21 cm long, but not longer than 25 cm. Is there an equivalent ratio for hands that is longer than 21 cm, but shorter than 25? By repeating the process from before to find an equivalent ratio, we can add 3 cm to the arm length while adding 7 cm to the foot length. OKAY! It looks like we've found what Mary's been looking for. 24 cm hands and 56 cm feet! Now that that's settled, all the monster needs is a head. All monsters have big heads, of course, so this is a great choice! Her monster is charged up and ready to leave with Mary! Mary helps him take his first steps! Now the only question is, which jungle gym will they go to first?