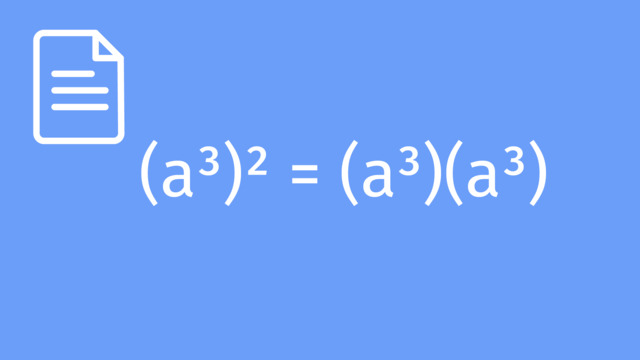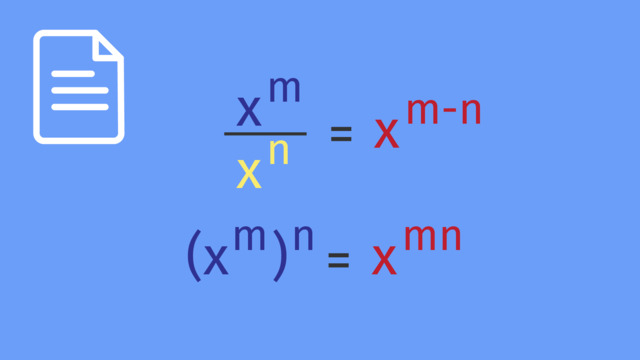Numbers Raised to the Zeroth Power
Basics on the topic Numbers Raised to the Zeroth Power
Numbers Raised to the Zeroth Power – Definition
Understanding the power of zero is an essential part of learning algebra. This concept is a piece of the broader puzzle of the laws of exponents, which are vital for simplifying expressions and solving equations involving exponential notation.
The power of zero may seem simple, but it plays a significant role in mathematical computations and has real-world applications in areas like computer science and engineering. By learning how numbers behave when raised to the power of zero, you're unlocking an important skill in mathematics.
The Power of Zero Rule states that any non-zero number raised to the power of zero equals one. In simpler terms, no matter what number you start with, if you raise it to the power of zero, the result is always one.
Numbers Raised to the Zeroth Power – Explanation
To truly grasp why anything raised to the power of zero is one, it's essential to understand the concept of exponents. Exponents indicate how many times a number, known as the base, is multiplied by itself. The power of zero is a unique case in this system.
Let’s take a look at some examples of problems involving a zeroth power.
Simplify: $\frac{m^{4}}{m^{4}}$
- Divide with same base: When we have the same base in both the numerator and the denominator, we subtract the exponents.
- Expansion: $\frac{m^{4}}{m^{4}} = m^{4-4}$
- Simplification: $m^{4-4} = m^{0}$
- Solution: $m^{0} = 1$
Simplify: $(m^{-3})(m^{3})$
- Multiply with same base: When we multiply powers with the same base, we add their exponents.
- Expansion: $(m^{-3})(m^{3}) = m^{-3+3}$
- Simplification: $m^{-3+3} = m^{0}$
- Solution: $m^{0} = 1$
Simplify: $\frac{5^{n}}{5^{n}}$ for any positive integer $n$
- General form: This represents a general case where any positive integer $n$ is the exponent.
- Divide with same base: Similar to the first problem, we subtract the exponents when dividing like bases.
- Solution: $\frac{5^{n}}{5^{n}} = 5^{n-n} = 5^{0} = 1$
Practice some own your own!
Numbers Raised to the Zeroth Power – Application
Evaluate $4^{x} \div 4^{x}$ when $x = 5$
- Substitute the value of $x$: Replace $x$ with 5 in the expression.
- Calculation: $4^{5} \div 4^{5}$
- Simplify: As the bases are the same, we subtract the exponents.
- Expansion: $4^{5-5} = 4^{0}$
- Solution: $4^{0} = 1$
Evaluate $(2^{x-1}) \times (2^{1-x})$ when $x = 3$
- Substitute the value of $x$: Replace $x$ with 3.
- Calculation: $(2^{3-1}) \times (2^{1-3})$
- Simplify: Add the exponents since the bases are the same.
- Expansion: $2^{2} \times 2^{-2} = 2^{2-2} = 2^{0}$
- Solution: $2^{0} = 1$
Evaluate $\dfrac{(5^{x})(5^{2x})}{5^{3x}}$ when $x = 2$
- Substitute the value of $x$: Replace $x$ with 2.
- Calculation: $\frac{(5^{2})(5^{4})}{5^{6}}$
- Simplify: Add exponents in the numerator and subtract from the exponent in the denominator.
- Expansion: $\frac{5^{6}}{5^{6}} = 5^{6-6} = 5^{0}$
- Solution: $5^{0}= 1$
Try some on your own!
Numbers Raised to the Zeroth Power – Summary
Key Learnings from this Text:
- Understanding the power of zero is crucial in algebra and simplifying expressions.
- The Power of Zero Rule, stating any non-zero number raised to the power of zero equals one, is a key concept in exponents.
- This rule is not just theoretical; it has practical applications in fields like computer science and engineering.
- Mastering this concept aids in developing a stronger grasp of mathematical principles and problem-solving techniques.
Numbers Raised to the Zeroth Power – Frequently Asked Questions
Transcript Numbers Raised to the Zeroth Power
Young Vaughn, a Greek scholar in training, is in the middle of his daily lesson. Vaughn has learned all about exponents, but he wants to know what happens when you raise a number to the zeroth power. His Sage has just told him that any non-zero number raised to the zeroth power equals one. But Vaughn is a man of logic, a scholar! He won't accept this explanation without proof. Let's help Vaughn use patterns, logic, and laws of exponents to prove the Sage's advice about numbers raised to the zeroth power. First, let's look at the exponential patterns of 2. 2 to the first power is 2, 2 to the second power is 4, 2 to the third power is 8, and 2 to the fourth power is 16. Do you notice any patterns in the bottom of our table? As our exponents increase from left to right the value increases by a multiple of two. That makes sense, because 2 is the base, and the exponent tells us how many times the number 2 is multiplied. But what happens when we move from right to left? Notice that we're going in the opposite direction of the multiplication. Therefore, we divide by two each time. So, let's continue our pattern to the left. 2 divided by 2 is 1, 1 divided by 2 is 1/2, 1/2 divided by 2 is 1/4. Now let's fill in the exponential notation where the exponent decreases by one when moving from right to left. That gives us 2 to the zeroth power 2 to the power of negative one and 2 to the power of negative 2. Both patterns do confirm that 2 to the zeroth power is 1. So far the Sage appears to be right. This was just a pattern but we can use a law of exponents to write our proof. Recall the quotient of powers law states that when you divide two powers... with the same base you subtract the exponents. For example, to simplify 5 to the 7th divided by 5 to the third we subtract the exponents, to arrive at 5 to the fourth. But what about this expression, 5 to the third divided by 5 to the third? Well, we know that any number divided by itself equals one. We can also apply the quotient of powers law and subtract the 3 from 3, this expression simplifies to 5 to the zeroth power. Therefore, we can see that 5 to the zeroth power equals one. So let's use the variable 'x' to represent any base except zero according to the definition of the zeroth power rule. Then let the variable 'm' represent any exponent. Using the same logic as before, we can see that any number divided by itself equals one. And applying the quotient of powers law and simplifying shows us that any non-zero number raised to the zeroth power equals one. So, the sage is still right, and we can believe him with our proof of the zeroth power. We can apply what we know about the zeroth power to all sorts of expressions, including ones that use the laws of exponents. Let's take a look at the expression: the quantity 'y' to the 6th power, all raised to the zeroth power. Which law of exponents do you recognize here? Using the law of powers of powers, we can multiply together the inner and outer exponents. We can see that gives us 'y' raised to the zeroth power is one. Notice that the zeroth power rule holds true. Any non-zero number raised to the zeroth power is one. Okay, what about five times 'x' squared times 'y' cubed, all raised to the zeroth power. We could expand it using the powers of products law then we multiply the exponents applying the powers of powers law simplify and finally notice that each term reduces to one using the zeroth power law. Giving us a result of one. Or we could recall that any non-zero number raised to the zeroth power is one. Therefore, identifying when the zeroth power law can be used will help you make dealing with exponents quicker. Let's review numbers raised to the zeroth power and applying it to other power laws. What is the zeroth power law? Any non-zero number raised to the zeroth power equals one. This law works no matter which law of exponents you're dealing with such as powers of powers of products or quotient of powers. Vaughn needed to use logical reasoning to prove the zeroth power law of exponents, and so did you! Vaughn continues his studies and becomes a great philosopher, thanks to his skepticism and use of logic and reasoning. People come from far and wide to hear him speak. Vaughn's definitely going down in history as one of the greats.
Numbers Raised to the Zeroth Power exercise
-
Recognize a pattern of exponential powers.
HintsThe large number is the base and the smaller number is called the exponent.
To solve, we multiply the base by itself by the number of times the value of the exponent is.
The expression $4^2$ would be $4 \cdot 4$, not $4 \cdot 2$.
$4^2 = 16$
If the exponent was negative, the result would be a multiplicative inverse.
For example, $4^{-2} = \frac{1}{16}$.
SolutionHere you will see the solutions to the pattern in this table.
-
Understanding the relationship between the Quotient Power Law and the Zeroth Power Law.
HintsTo further prove the Quotient Powers Law, a number in exponential notation can also be expanded to show why we subtract.
$\dfrac{k^8}{k^4} = \dfrac{(k)(k)(k)(k)(k)(k)(k)(k)}{(k)(k)(k)(k)}$
The $k$s can cancel out, which essentially is $8-4$.
The result is $k^4$.
Another way to think about the Zeroth Power Law is to recognize that anything divided by itself is always $1$.
For example...
$\dfrac{7}{7}=1$
$\dfrac{7^4}{7^4}=1$
$\dfrac{w^3}{w^3}=1$
SolutionThe Quotient of Powers law states that when you have the same base, you can subtract the exponents. For example $\dfrac{k^8}{k^4}$ would be $\bf{k^{8-4}}$, resulting in $k^4$.
${}$
The Zeroth Power law states that anytime you have an exponent of $0$, and the base does not equal zero, the solution is always $\bf{1}$. For example, $\dfrac{k^8}{k^8}$, would be $\bf{k^{8-8}}$ resulting in $k^0$, which is equal to $1$.
-
Identify the Laws of Exponents that relate to the Zeroth Power Law.
HintsAn example of the Zeroth Law being applied:
$g^0=1$
- Any number raised to the power of $0$ is equal to $1$.
An example of the Quotient of Powers Law being applied:
$\dfrac{h^7}{h^2}=h^5$
- When there are like bases, keep the base and subtract the exponents.
An example of the Product of Powers Law being applied:
$j^2 \cdot j^7 = j^9$
- When there are like bases, keep the base and add the exponents.
An example of the Power of a Power Law being applied:
$(f^2)^{5}=f^{10}$
- When there is a power being raised to another power, multiply the exponents.
SolutionZeroth Power Law: $n^0 = 1$
Any number raised to the power of zero equals one.
Quotient of Powers Law: $\dfrac{n^5}{n^2}=n^{5-2}=n^3$
When dividing like bases, subtract the exponents.
Product of Powers Law: $n^4 \cdot n^3 = n^{4+3} = n^7$
When multiplying like bases, add the exponents.
Power of a Power Law: $(n^3)^{4}=n^{(3)(4)}=n^{12}$
For a power raised to another power, multiply the exponents.
-
Apply the Zeroth Power Law.
HintsThese examples may help you find the solution.
The Power of a Power Law states that when you have a power raised to another power, the powers will be multiplied.
$(n^5)^{3}=n^{(5)(3)}=n^{15}$
SolutionThe solution to $(3a^4b)^{0}$ would be $\bf{1}$.
If you apply the power of a power law, each exponent inside the parentheses would be multiplied by $0$, and since anything multiplied by zero is zero, all the exponents in the parentheses would change to $0$.
$3^0a^0b^0$ = $1$
The Zeroth Power Law then states that any number raised to the power of zero is equal to one.
-
Apply the Zeroth Power Law to expressions in exponential notation.
HintsThe Zeroth Power Law states that any value raised to the zeroth power will result in a positive one.
As long as the base is not zero, this rule will apply.
SolutionEach solution will be $1$, since each example has a base that is not zero, and an exponent of zero.
$3^0 = 1$
${}$
$e^0 = 1$
${}$
$999^0 = 1$
${}$
$(-d)^0 = 1$
-
Apply your understanding of the Zeroth Power Law.
HintsThe Laws of Exponents will be useful when simplifying expressions in exponential notation.
Remember also the Product of Powers Law states that when you multiply two expressions with like bases, you add the exponents.
For example: $(x^3)(x^2)$ we would add the 3 and 2 to find a final solution of $x^5$
If one of those exponents were negative, we would do the same, but use what you know about adding integers.
For example: $(x^{-3})(x^2)$ we would add the $-3$ and $2$ to get a result of $-1$ or $x^{-1}$
Solution- Anything with a power of zero will result in 1 as a solution.
$(5g^3)^0=1$
$(-9)^0=1$
$\dfrac{n^6}{n^6}=1$
$z^0 = 1$
$(n^{-2})(n^2)=1$
${}$
- If the exponent is not equal to zero, then the solution is not one.
$b^1=b$