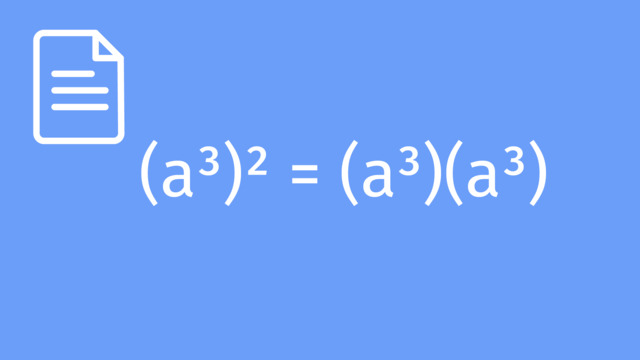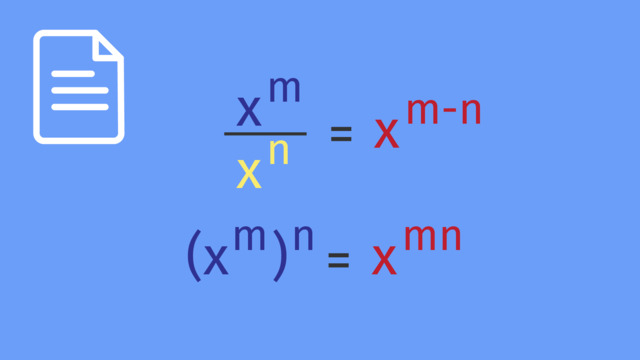The Definition of Negative Exponents
Basics on the topic The Definition of Negative Exponents
Negative Exponents – Introduction
Negative exponents are an essential concept in algebra, often encountered in scientific notation, algebraic expressions, and real-world scenarios such as calculating decay rates or understanding exponential growth in finance. A negative exponent indicates repeated division, contrary to a positive exponent, which denotes repeated multiplication.
A negative exponent expresses how many times the reciprocal of the base is multiplied by itself. For instance, $a^{-n}$ means $1$ divided by $a$ multiplied by itself $n$ times.
Negative Exponents – Explanation
The shift from positive to negative exponents represents a transition from multiplication to division in terms of how we handle the base number. With positive exponents, like $a^{3}$, we multiply the base ($a$) by itself a certain number of times (three times here). However, with negative exponents, such as $a^{-3}$, it indicates division. Instead of multiplying the base, we divide $1$ by the base multiple times. This reflects the inverse relationship - while positive exponents grow the number, negative exponents reduce it reciprocally.
Example:
- Positive Exponent: $2^{3} = 2 \times 2 \times 2 = 8$
- Negative Exponent: $2^{-3} = \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8}$
Practice converting negative exponents to positive exponents.
The Laws of Exponents
To understand the definition of negative exponents, it is important to understand the proofs of laws of exponents. Here, you will see all the important laws of exponents, including the law of negative exponents!
| Law | Mathematical Representation | Description |
|---|---|---|
| Product of Powers | $a^{m} \times a^{n} = a^{m+n}$ | When multiplying like bases, add the exponents. |
| Quotient of Powers | $\frac{a^{m}}{a^{n}} = a^{m-n}$ | When dividing like bases, subtract the exponents. |
| Power of a Power | $(a^{m})^{n} = a^{mn}$ | When raising a power to a power, multiply the exponents. |
| Zero Exponent | $a^{0} = 1$ (where $a \neq 0$) | Any non-zero number raised to the power of zero is one. |
| Negative Exponent | $a^{-n} = \frac{1}{a^{n}}$ | A negative exponent indicates the reciprocal of the base raised to the positive exponent. |
Let’s practice applying these laws of exponents and specifically involving negative exponents.
Product of Powers: Simplify $2^{-3} \times 2^{-2}$.
- Add the exponents: $2^{-3} \times 2^{-2} = 2^{(-3)+(-2)} = 2^{-5}$.
- Convert to a positive reciprocal: $2^{-5} = \frac{1}{2^{5}} = \frac{1}{32}$.
Quotient of Powers: Simplify $\frac{3^{-4}}{3^{-2}}$.
- Subtract the exponents: $\frac{3^{-4}}{3^{-2}} = 3^{-4-(-2)} = 3^{-2}$.
- Convert to a positive reciprocal: $3^{-2} = \frac{1}{3^{2}} = \frac{1}{9}$.
Power of a Power: Simplify $(5^{-2})^{3}$.
- Multiply the exponents: $(5^{-2})^{3} = 5^{-2 \times 3} = 5^{-6}$.
- Convert to a positive reciprocal: $5^{-6} = \frac{1}{5^{6}}$.
Try some on your own!
Understanding Negative Exponents with Expansion
Expanding an expression written in exponential notation can help us better visualize how negative exponents work.
Expand and simplify the expression:
$\dfrac{5^{3}}{5^{7}}$
Expand Both Exponents:
- Numerator $5^{3}$ as $5 \times 5 \times 5$
- Denominator $5^{7}$ as $5 \times 5 \times 5 \times 5 \times 5 \times 5 \times 5$
Divide Step by Step:
- Each $5$ in the numerator cancels out a $5$ in the denominator.
- Left with $\frac{1}{5 \times 5 \times 5 \times 5}$ (four $5$'s remain in the denominator).
Result After Cancelation: $\dfrac{1}{5^{4}}$
Practice some expanding and working with negative exponents on your own
Negative Exponents – Summary
Key Learnings from this Text:
- Negative exponents represent reciprocal values and repeated division.
- Understanding and applying exponent rules is crucial for simplifying expressions.
- Expanding negative exponents helps to understand their meaning visually.
- Converting negative exponents to positive exponents simplifies the expression.
Definition of Negative Exponents – Frequently Asked Questions
Transcript The Definition of Negative Exponents
Wheezy, Macaroni, and Pipsqueak are starting to notice a disturbing trend. The iceberg where they love to play keeps breaking in half! It's a repeated-division catastrophe! Fortunately, Professor Penguin is on hand to explain using the definition of negative exponents. Let's take a closer look at how the iceberg is breaking apart. We started with one iceberg. Dividing this iceberg in half gives use two icebergs that are one-half the size of the original. But the icebergs continue to split in half. One-half of the original, divided by two, gives us one-fourth. One-fourth divided by two gives us one-eighth. So after 3 rounds of splitting in half, each mini-iceberg is one-eighth the size of the original. How small would each berg be after 6 rounds of splitting in half? We can answer this question by looking at exponents and division. You should already be familiar with the Law of Quotients of Powers, which tells us how to divide numbers written in exponential notation, when they both have the same base. For example, how would you simplify 2 to the 5th over 2 squared? When dividing numbers with the same base, we subtract the exponents. So this expression can be simplified to 2 cubed. But let's take a look at what happens if we have a larger exponent in our denominator than in our numerator. To simplify 2 to the fifth divided by 2 to the eighth we subtract the exponents and are left with 2 to the negative third power. But what does that mean? If we write our numerator and denominator in their factored forms and then cancel we can see that 1 over 2 to the third power is the same as 2 to the negative third power. In general, this is how we define negative exponents: x' to the negative 'n' equals 1 over 'x' to the 'n'. So while positive exponents represent repeated multiplication, negative exponents represent repeated division. This will come in handy, since we always want to write numbers without a negative exponent when simplifying. So let's go back to our iceberg. Originally, we had one whole iceberg. After one round of dividing in half, one mini-berg is half the size of the original, which we can write as 2 to the negative first power. After two rounds of dividing, that's 1 over 2 squared, or 2 to the negative second power. After 3 rounds it's one over 2 to the third, or 2 to the negative 3. We want to know how small are the mini-bergs after dividing by 2, six times. How could we write that using negative exponents? Well we're dividing by two over and over again, so that number is our base. And we're going to divide six times, so our exponent is negative 6. Using the definition of negative exponents we can write this as a fraction and see that each mini-berg is one sixty-fourth of the original. “Let's look at three quick examples to see how negative exponents apply to what you already know about the Laws of Exponents." Our first example uses the Product of Powers Law. Four to the negative 3rd times four to the negative 5th. We are multiplying numbers with the same base, so what should do with the exponents? Adding the exponents, gives us 4 to the negative eighth power. We don't want to leave this number with a negative exponent, so we use the definition of negative exponents to simplify to the fraction one over 4 to the 8th. Now an example of the quotient of Powers Law. Three to the negative 1st over three to negative the 7th. Here we are dividing numbers with the same base, so what should we do with the exponents? The Quotient of Powers Law tells us to subtract the exponents, so negative 1 minus negative 7 is equal to negative 1 plus 7. Leaving us with 3 to the 6th power. Our third and final example is a number raised to a power, then raised to a power again. What does the Powers of Powers Law tell us to do with the exponents in this case? A power raised to a power means we multiply exponents. Negative 3 times 2 is negative 6. Because we don't want to leave this number with a negative exponent, we rewrite eight to the negative 6th as one over 8 to the 6th power. Let's review. While positive exponents are how we represent repeated multiplication negative exponents represent repeated division. In general, we define a negative exponent as 'x' to the negative 'n' is equal to one over 'x' to the 'n'. And remember, the laws of exponents apply to all numbers written in exponential notation. This includes Product of Powers Quotient of Powers and Powers of Powers. Uh oh, it looks Professor Penguin got a bit carried away with splitting those icebergs in half. I think we're gonna need another iceberg!
The Definition of Negative Exponents exercise
-
Simplify the powers.
HintsWhen we multiply exponents with the same base we use the product of powers rule.
For example, $5^3\times5^2 = 5^{3+2} = 5^5$
We add the exponents.
When we divide exponents with the same base we use the quotient of powers rule.
For example, $\dfrac{7^6}{7^4} = 7^{6-4} = 7^2$
We subtract the exponents.
When subtracting negatives we can use a number line.
For example $-3 - (+2) = -3 - 2 = -5$
Solution- $3^4\times3^2 = 3^{4+2} = 3^6$
- $3^7\times3^{-2} = 3^{7-2} = 3^5$
- $\dfrac{3^8}{3^4} = 3^{8-4} = 3^4$
- $\dfrac{3^{-2}}{3^4} = 3^{-2-+4} = 3^{-2-4} = 3^{-6}$
-
Simplify the negative exponent.
HintsThe rule we are using states that a negative power is the same as $1$ over the positive power.
If a negative power is equal to $1$ over the positive power then $8^{-5} = \dfrac{1}{8^5}$
Solution$9^{-3} = \dfrac{1}{9^3}$
$9^{-2} = \dfrac{1}{9^2}$
$9^{-1} = \dfrac{1}{9}$
$9^{-4} = \dfrac{1}{9^4}$
-
Calculate the product of negative powers.
HintsFor the product of powers we add the powers when the base is the same.
Example shown.
If we have added the powers and we get a negative power. We know that a number to the negative power is equal to one over the number to the positive power.
This should be done to simplify further.
Solution$\mathbf{\frac{1}{3^6}}$
- We use the product of powers rule, adding the powers
- Negative power is $1$ over the positive power
-
Calculate the quotient of negative powers.
HintsWhen subtracting negative numbers subtracting a negative means to add.
For example $-7 - (-3) = -7 + 3 = -4$
For the quotient of powers we subtract the powers when the base is the same.
Example shown.
When we have subtracted the powers, we get a negative power.
We know that a number to the negative power is equal to one over the number to the positive power.
This should be done to simplify further.
Solution$\dfrac{1}{5^4}$
- We use the quotient of powers rule, subtracting the powers
- Subtracting a negative is the same as adding
- Negative power is $1$ over the positive power
-
Calculate the quotient of negative powers.
HintsTo work this out we subtract the powers which gives us a negative power.
We then use the definition of negative exponents.
A number to a negative power is equal to $1$ over the number with a positive power. See the example.
If we had $\dfrac{8^2}{8^7}$ we subtract the powers first.
$2 - 7 = -5$
Our answer is $8^{-5} = \dfrac{1}{8^5}$.
We can see the example where we use repeated division to show this.
SolutionAnswer $\dfrac{1}{5^3}$
- We subtract the powers first.
- $3 - 6 = -3$
- Our answer is $5^{-3}$
- By using repeated division shown = $\dfrac{1}{5^3}$.
-
Calculate the power of negative powers.
HintsA positive number $\times$ negative number $=$ negative answer.
For example $8\times(-2) = -16$.
For the power of powers we multiply the powers when the base is the same.
Example shown.
If we have multiplied the powers and the answer is a negative power.
We know that a number to the negative power is equal to one over the number to the positive power.
This should be done to simplify further.
Solution$\dfrac{1}{9^{12}}$
- We use the power of powers rule, multiplying the powers
- positive $\times$ negative $=$ negative
- Negative power is $1$ over the positive power