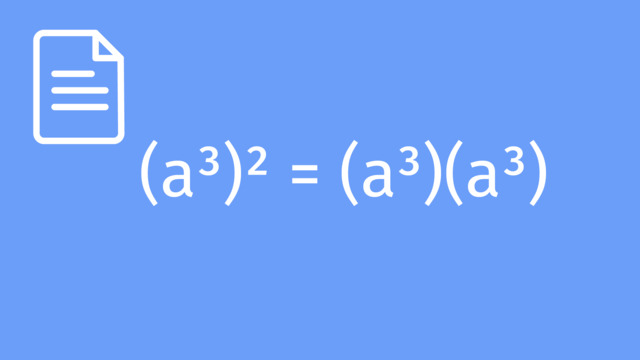Exponents with Negative Bases


Basics on the topic Exponents with Negative Bases
Exponents with Negative Bases – Introduction
When we delve into the world of mathematics, we encounter various operations that extend beyond simple addition and subtraction. One such operation is the use of exponents, which are not only efficient but also foundational in understanding higher-level math concepts. Exponents with negative bases, on the other hand, add a twist to the conventional rules and require a keen understanding, especially when interpreting and solving complex problems. Let's uncover the nuances of exponents, particularly focusing on those with negative bases.
Exponents with Negative Bases – Definition
Exponents provide a shorthand notation for indicating how many times a number, known as the base, is multiplied by itself. The exponent, written as a superscript number, represents the count of multiplications. For instance,$4^{3}$ is the same as saying $4 \times 4 \times 4$, which simplifies to $64$. But what happens when we introduce a negative base into the mix?
If you're discussing how a negative base affects the outcome when raised to an exponent, remember: - If the exponent is an even number, the result is positive because the negative signs cancel out. For example, $(-4)^{2} = 16$. - If the exponent is an odd number, the result is negative because there's one unmatched negative sign. For example, $(-4)^{3} = -64$.
Negative bases refer to numbers less than zero that are raised to a power. The outcome of an exponentiation involving a negative base hinges on whether the exponent is even or odd.
- Even Exponents: An even number of negative multiplications will result in a positive product because each pair of negative numbers multiplies to a positive.
- Odd Exponents: An odd number of negative multiplications will yield a negative product since there will always be one unpaired negative number.
Exponents with Negative Bases – Example
Let's look at an example to clarify:
With an Odd Exponent: $(-3)^{3}$ simplifies to $-3 \times -3 \times -3$, which equals $-27$.
With an Even Exponent: $(-3)^{2}$ simplifies to $-3 \times -3$, which equals $9$.
These examples illustrate the fundamental difference in outcomes based on the parity of the exponent.
Exponents with Negative Bases – Practice
Exponents with Negative Bases – Summary
Key Learnings from this Text:
- Exponents provide a concise way of representing repeated multiplication.
- A negative base raised to an even exponent results in a positive number.
- A negative base raised to an odd exponent results in a negative number.
Feel encouraged to explore other content on our educational platform, including interactive practice problems, videos, and printable worksheets to support your journey through the fascinating landscape of mathematics.
Exponents with Negative Bases – Frequently Asked Questions
Transcript Exponents with Negative Bases
What do you think is a negative one to the power of one hundred a positive or negative answer? Let's explore 'exponents with negative bases' to find out the answer to that question. If you remember, exponents can always be expanded in order to find a solution. Negative one times negative one times negative one times negative one times negative one. Yeah, this is going to take forever there has to be a quicker way to determine if the solution is negative or positive! Let's break it down with a smaller exponent. Negative one to the fifth power, expanded would look like this. Notice the negative ones stay in parenthesis so we remember they are all negative. We can multiply a negative one by a negative one, to get a positive one. The now positive one, times a negative one, is back to a negative one. Again, negative one times negative one is positive one. And finally, positive one times negative one is negative one. Let's try another example, and see if we can identify a pattern. Negative one to the fourth power. Just like before, we can expand and start multiplying this one at a time. Negative one times itself is positive one. That times a negative one brings it back to negative one. And finally, a negative one times itself is a positive one. If you noticed, when our exponent was five, which is an odd number, the result was negative. And when our exponent was four, an even number, the result was positive. Using this pattern, let's try a some more. Negative one to the ninth power. Would it be a negative or a positive solution? Since nine is an odd number, the solution will be a negative answer. Would negative one to the power of twenty be a positive or negative solution? Twenty is an even number, so the solution will be a positive one. Here is another to try, but look closely and see if you can spot the difference. You may quickly say this is a positive solution since eight is an even number, but that is actually not correct! The negative one is not included in a grouping symbol, like parentheses, and this will change things up! If we expanded this, we would not be multiplying negative ones, but rather positive ones, like this. The negative sign in front, since not inside a parentheses with the one, is separate. If we follow the order of operations to solve this, we would first perform the exponent, which is one to the eighth power. This is equal to a positive one. But then the negative is applied like multiplication, and the solution becomes negative. So, where there are no parentheses we must remember the base is positive, and the negative sign is applied at the end. Let's summarize! Back to the original question: would negative one to the power of one-hundred be negative or positive? We learned when we have a negative base and an even exponent, our solution is always positive. And when we have a negative base, but an odd exponent, the solution is negative. Based on this pattern we discovered, the solution must be positive since one-hundred is an even number!
Exponents with Negative Bases exercise
-
Understand the rule to determine the sign of a negative number with an exponent.
HintsIf you ever forget the rule and are unsure if an expression in exponential notation with a negative base is positive or negative, you can always expand the expression.
For example:
$(-3)^4 = (-3)(-3)(-3)(-3)$
When you have very large exponents, this may not be efficient, so the rule will then be useful.
- When the base is negative and you have an even exponent, the solution is positive.
- When the base is negative and you have an odd exponent, the solution is negative.
SolutionSince $(-1)^{100}$ has an even exponent of $\bf{100}$, it is equal to a positive one. The rule states that when there is a negative base, and the exponent is even, the result is always positive.
For this example, $(-1)^{101}$ has an odd exponent of $101$, it is equal to a negative one. The rule states that when there is a negative base, and the exponent is odd, the result is always negative.
The solution to $(-1)^{200}$ is 1.
The solution to $(-1)^{199}$ is -1.
-
Determine the sign of an exponent with a negative base.
HintsWhen there is a negative base, the exponent will determine whether the solution will be positive or negative.
Even Exponent = Positive Solution
Odd Exponent = Negative Solution
Here is an example to help you:
$(-2)^4$
The exponent of $4$ is even which will make our solution positive.
$(-2)^7$
The exponent of $7$ is odd which will make our solution negative.
SolutionPositive Solutions $(-3)^2$ $(-11)^8$ $(-5)^{10}$ $(-1)^{12}$
Negative Solutions $(-2)^3$ $(-9)^{19}$ $(-5)^5$ $(-10)^9$
-
Applying your knowledge of exponential notation.
HintsThe rule states that when you have a negative base and an exponent follow these guidelines for determining the sign of the solution.
If you are using a calculator to check your solution, be sure to include the parentheses sign.
The expression can be expanded to $(-2)(-2)(-2)(-2)(-2)$.
First multiply the first two $(-2)(-2)=4$ and then continue with the remaining $(-2)$s.
Solution$(-2)^5 = \bf{-32}$
This expression can be expanded: $(-2)(-2)(-2)(-2)(-2)$.
Since this expression with a negative base, has an odd exponent, the solution must be negative.
The solution can be found by multiplying $-2$ by itself $5$ times.
-
Identify characteristics in exponential notation that can determine a solution's sign.
HintsUsing a set of parentheses is super important when it comes to exponents.
$(-1)^8$ and $-1^8$ are not the same thing.
$(-1)^8$ expanded: $(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)$
$-1^8$ expanded: $- (1)(1)(1)(1)(1)(1)(1)(1)$
$(-1)^8 = 1$
$-1^8 = -1$
SolutionHere are the matches.
$(-3)^2=9$
$-3^2=-9$
$(-1)^8=1$
$(-6)^1=-6$
$-1^8=-1$
$(-6)^2=36$
-
Understand what it means to expand an expression in exponential notation.
HintsNumbers written in exponential notation are made up of a base and an exponent.
In $(-1)^7$, $\bf{(-1)}$ is the base and $\bf{7}$ is the exponent
Numbers written in exponential notation can be expanded.
In $(-1)^7$, we are multiplying $\bf{(-1)}$ by itself seven times.
SolutionThe base is $(-1)$ and the exponent is $7$. This means that the $(-1)$ is multiplied by itself $7$ times and can be expanded like this:
$\bf{(-1)(-1)(-1)(-1)(-1)(-1)(-1)}$
-
Compare quantities in exponential notation with negative bases.
HintsExamples of Inequality Symbols:
4 > -1
-3 < 8
-5 = -5
Use what you have learned about negative bases with an exponent.
Take a look at this example to help you!
$(-2)^4$ ? $(-5)^5$
${}$
$(-2)^4$ > $(-5)^5$
${}$
$16$ > $-3,125$
Solution$(-2)^3$ < $(-2)^1$
- $-8$ < $-2$
$(-3)^2$ > $(-3)^3$
- $9$ > $-27$
$(-x)^2$ > $(-x)^9$
- "a positive value" > "a negative value"
${}$
$(-1)^4$ = $(-1)^8$
- $1$ = $1$