Standard Form
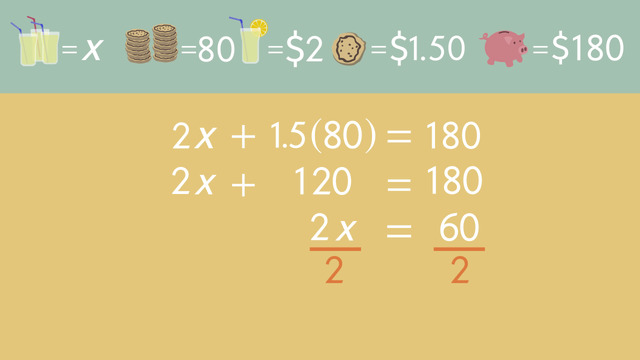

Basics on the topic Standard Form
When writing linear equations, the equation can be written in more than one form. Most common is the slope-intercept form, but point-slope form and standard form (general form) also have advantages. To answer linear equation problems, how do you know which form to use?
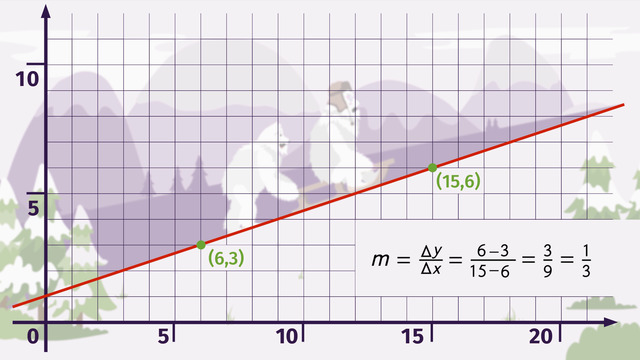
That depends on the unknown value, and this is why you must understand all the forms. For this video, we will explore the standard form of linear equations. The standard form of a linear equation is: Ax + By = C. There are some restrictions for the use of this form. Both A and B cannot be equal to zero at the same time, both A and B must be integers, and usually A is a positive number. To understand the real value of this form, graph the information.
You will see the graph shows all the combinations possible combinations of x and y to sum to the constant – the C-value. The x-intercept at point ( x, 0 ) is the maximum value for x, and the y-intercept at point ( 0, y ) is the maximum point for y. The standard form is valuable in the real world for situations when you need to figure out the combinations of two variables to sum to a constant. To learn more about the standard form of linear equations, sit back, relax, and take a look at this video.
Use slope to create equations of the line.
CCSS.MATH.CONTENT.HSG.GPE.B.5
Transcript Standard Form
Kayla runs a lemonade and chocolate chip cookies stand during summer vacation to make some money.
She has just sold her last cup of lemonade for the day. She made a total of $180 and sold 80 chocolate chip cookies.
Kayla wants to know how many cups of lemonade she has sold to prepare for tomorrow's sales.
Writing the Equation in Standard Form
A linear equation in standard form can be used to find the number of cups of lemonade.
The standard form of a linear equation is Ax + By = C, where A and B cannot both equal zero.
Let's use x to represent the number of cups of lemonade sold and y for the number of cookies sold.
- We also know that the cost per cup of lemonade is 2 dollars.
- And that Kyla sells her cookies for 1 dollar and 50 cents each.
- We also know that Kyla sold a combined hundred eighty dollars' worth of cookies and lemonade.
Our coefficients in this example are the prices we know. So 2 can be substituted in for A. Now we have an expression that represents the money earned from the lemonade: 2x.
$1.50 can be substituted in for B. 1.5y stands for the money earned from the cookies.180 can be substituted in for C. This represents Kyla's sales total for the day. So our expression to find the number of cups of lemonade Kayla sold, written in standard form, is 2x + 1.5y = 180.
Solving the Linear Equation
Since we know Kyla sold 80 cookies, we can plug this into y. Now we can solve the equation for x in order to find the number of cups of lemonade Kyla sold.
- The first step is to multiply 1.5 and 80 together, giving us 120. Remember, 120 is the total money Kyla earned from selling cookies.
- The next step is to subtract 120 from both sides of the equation, leaving us with 2x = 60.
- The last step is to divide both sides of the equation by 2, leaving us with x = 30. So now we know Kayla sold 30 cups of lemonade today.
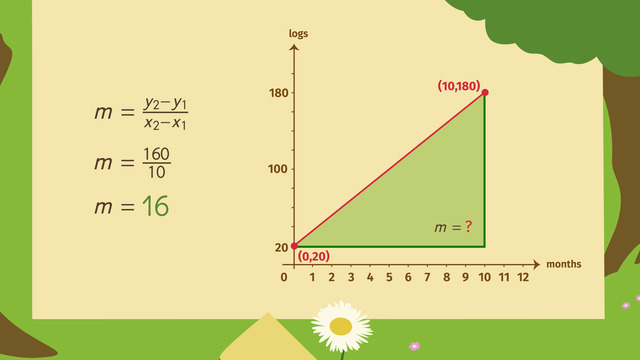
Graphing Linear Equations in Standard Form
A linear equation in standard form can also be graphed to determine the number of cups of lemonade and cookies sold for 180 dollars. The linear equation produces all possible combinations of lemonade and cookie sales that would yield $180 including negative values.
The part of the graph we need to focus on is in the first quadrant where x and y are positive. The x- and y-intercepts can be used to find the starting point and ending point for the number of items sold.
The x-intercept will show the maximum amount of lemonade that can be sold for $180. The y-intercept will show the maximum amount of cookies that can be sold for $180.
Finding the X-Intercept
The first step is to find is the x-intercept. This is the point that crosses the x-axis when y is 0. This means we should substitute y in the equation with 0.
Since anything times 0 equals 0, this leaves us with the equation 2x = 180. The last step is to divide both sides of the equation by 2, giving us x equals 90. Now we have our x-intercept. And we can graph the ordered pair of (90, 0) on the coordinate plane.
Finding the Y-Intercept
The second step is to find is the y-intercept. This is the point that crosses the y-axis when x is 0. This means we should substitute x in the equation with 0. Since anything times 0 equals 0, this leaves us with the equation 1.5y = 180.
The last step is to divide both side of the equation by 1.5 giving us y equals 120. Now, we have our y-intercept. So we can graph the ordered pair of (0, 120) on the coordinate plane.
Example Solutions
We can use the graph to see how many cups of lemonade sold when she sold 80 cookies. When y equals 80, we look at our line and see that x equals 30 cups of lemonade.
We can use the graph to see the relationship between the number of cups of lemonade and number of cookies sold for Kayla to make $180.
Another example is Kayla would have made $180 by selling 60 cups of lemonade and 40 cookies.
The next day Kayla comes to open her stand. Oh no! All of the neighborhood kids want to get in on her profit!
Standard Form exercise
-
Determine the number of glasses of lemonade that are sold.
HintsThe standard form:
$Ax+By=C$
$A\neq 0$ and $B\neq 0$.
In this example, $A=2$ and $B=1.5$ are the known prices.
To solve an equation, first simplify by combining like terms, and then isolate the variable using opposite operations.
SolutionTo write the in standard form:$Ax+By=C$, consider the facts.
- $x$ is the unknown number of sold glasses of lemonade.
- $y$ is the number of sold cookies.
- $A=2$ is the price of one glass of lemonade.
- $B=1.5$ is the price of one cookie.
- $C=180$ is the total amount Kayla earned that day.
$2x+1.5y=180$.
Since we already know the number of sold cookies ($80$), we can substitute $y$ with this number:
$2x+1.5\times 80=180$.
Now we can solve the equation:
$\begin{array}{rclrl} 2x+1.5\times 80&=&~~~180&&|\text{ multiplying}\\ 2x +120&=&~~~180\\ \color{#669900}{-120}&&\color{#669900}{-120}\\ 2x&=&~~~~~60 \end{array}$
Finally we divide both sides of the equation by $2$:
$x=30$.
Now we know that Kayla sold 30 glasses of lemonade.
-
Describe how to graph the equation.
HintsMultiplying by $0$ always equals $0$.
To solve the equation $3x=12$, you have to divide by $3$.
Each point $P(p_x,p_y)$ has an x-($p_x$) and a y-coordinate ($p_y$).
SolutionTo graph the equation $2x+1.5y=180$, let's evaluate the intercepts:
- for the y-intercept substitute $0$ for $x$
- for the x-intercept substitute $0$ for $y$
- $2(0)+1.5y=180$
- $2(0)=0$, so we get $1.5y=180$
- divide by $1.5$ to get $y=120$
- the y-intercept is $(0,120)$
- $2x+1.5(0)=180$
- $1.5(0)=0$, so we get $2x=180$
- divide by $2$ to get $x=90$
- the x-intercept is at $(90,0)$
-
Decide how many marbles and colored pencils Sue can buy.
Hints$x$ represents the number of colored pencils, and $y$ represents the number of marbles.
Write the equation in standard form:
$\begin{array}{c|c|c|c|c} A&x&B&y&C\\ 1&x&0.5&y&10. \end{array}$.
The equation for this situation written in standard form: $x+0.5y=10$.
Use a graph to verify each combination.
Use this graph to verify the combinations.
SolutionLet's start by using the standard form of an equation:
$Ax+By=C$.
- $x$ represents the unknown number of colored pencils.
- $y$ represents the unknown number of marbles.
- $A=1$ is the price for one colored pencil.
- $B=0.5$ is the price for one marble.
- $C=10$ is the total amount of Sue's pocket money.
$x+0.5y=10$.
The corresponding graph can be seen on the right side.
Let's check the combinations of pencils and marbles:
10 pencils and 5 marbles.
The point $(10,5)$ doesn't lie on the line. This isn't a solution of the equation.
$~$
5 pencils and 10 marbles
The point $(5,10)$ lies on the line. Let's calculate:
$5+0.5\times 10=5+5=10$ $\surd$.
$~$
6 pencils and 8 marbles
The point $(6,8)$ lies on the line, so it's a correct answer:
$6+0.5\times 8=6+4=10$ $\surd$.
$~$
8 pencils and 6 marbles
The point $(8,6)$ doesn't lie on the line, so it can't be an answer to the equation.
$~$
12 pencils and 4 marbles
The point $(12,4)$ doesn't lie on the line.
$~$
4 pencils and 12 marbles
The point $(4,12)$ lies on the line:
$4+0.5\times 12=4+6=10$ $\surd$.
-
Explain how you can determine the number of large scoops of ice cream.
HintsWe know the price and the number of the small scoops, but we don't know the number of the large scoops.
Write an equation in standard form: $Ax+By=C$.
To check your solution, you can substitute $y=5$ and $x$ into the equation written in standard form.
SolutionWe already know the price of a large scoop: $\$1.50$
The corresponding number of scoops is unknown. So let's assign $x$ to this number. So we can write the term:
$1.5 \times x$ which represents the total cost of large scoops.
For the small scoops, the price as well as the number of scoops are known. So we get the equation:
$0.9\times 5=4.5$
So the total costs for 5 small scoops of ice cream is $\$4.50$.
Adding the two terms we get the expression:
$1.5x+4.5$
This represents the total cost for the ice cream. Because Sue has $\$9$ to spendl, we can write and solve the following equation:
$1.5x+4.5=9$
Subtract $4.5$ on both sides of the equation and rewrite as:
$1.5x=4.5$
Dividing both sides by $1.5$ is equal to the solution for x:
$x=3$
Therefore, Sue can buy three large scoops of ice cream for herself to eat.
-
For standard form, determine all parts of the equation.
HintsUse this pattern
$\begin{array}{c|c|c|c|c} \text{price for lemonade}&\text{number of glasses}&\text{price for cookie}&\text{number of cookies}&\text{total}\\ 2&x&?&?&? \end{array}$
You already know which variable is assigned to the number of glasses and which to the number of cookies.
Use the following pattern:
$\begin{array}{c|c|c|c|c} \text{price for lemonade}&\text{number of glasses}&\text{price for cookie}&\text{number of cookies}&\text{total}\\ A&x&B&y&C \end{array}$
SolutionAn equation in standard form looks like this:
$Ax+By=C$
- $x$ is the unknown number of sold glasses of lemonade
- $y$ is the unknown number of sold cookies
- $A=2$ is the price for one glass of lemonade
- $B=1.5$ is the price for one cookie
- $C=180$ is the total amount Kayla earned that day
$2x+1.5y=180$
Since we know that Kayla sold 80 cookies, we can substitute $y$ with $80$ then we can rewrite the equation:
$2x+1.5\times 80=180$
-
Decide which equation in standard form corresponds to the graph.
HintsUsing the standard form, there are many combinations of x and y to write the equation of a line.
For this line the intercepts are at $(0,16)$ and $(20,0)$.
SolutionWrite an equation in standard form, $Ax+By=C$, for the given line.
Let's look at the intercepts, $(20,0)$ and $(0,16)$:
- if we plug in $x=20$ and $y=0$, we get $20\times A=C$
- for $(0,16)$ we get $16\times B=C$
- now we choose any value for $C$, for example $C=320$
- then we get $A=16$ and $B=20$
- One possible equation is $16x+20y=320$
We can say that any multiple of the equation $16x+20y=320$ is the same line that is graphed on the right:
- $0.8x+y=16$
- $2x+2.5x=40$
- and so on