Slope

Basics on the topic Slope
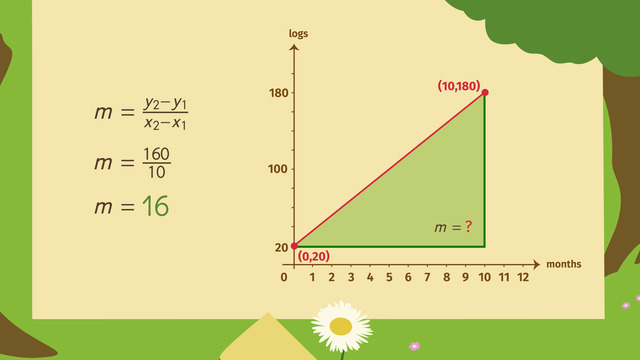
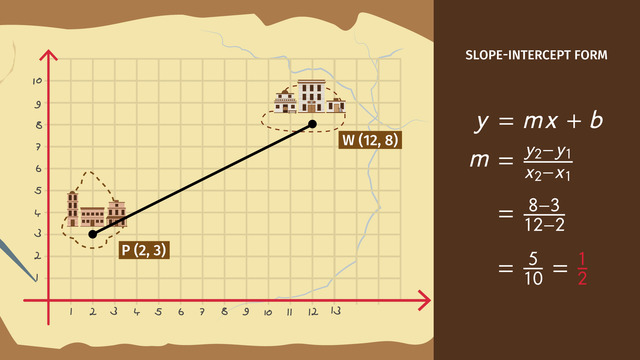
Slope measures the incline of a line. You can also think of this as the number that represents the steepness of a line. To calculate the slope, you can use the slope formula which is the change in the height compared to the change in the width. Using ordered pairs, this is the change in the y-values divided by the change in the x-values or the rise divided by the run.
How can you use the value of slope to compare the steepness of lines? The greater the absolute value of the slope, the more steep the incline. Slopes can be positive or negative. Often students are told to remember this information using a mountain analogy (let’s hit the slopes!).
For a positive slope, the line goes up the mountain and for negative slopes, the lines go down the mountain. I am positive it is more difficult to walk up a mountain – do you get my drift? What if there is no incline? Then the slope is zero, and if the line is vertical, the slope is not defined. Does this seem like a lot to remember? Watch this video on slope, and you will learn some helpful tips to remember this very important information, so you won’t go bombing on the Bunny Slope.
Use slope to create equations of the line. CCSS.MATH.CONTENT.HSG.GPE.B.5
Transcript Slope
On the slopes of the Himalayans, Leonetti the Yeti and his wife Betty are sledding. While Leonetti pushes his wife up the mountain, she nags at him to go faster. It’s hard work, and Leonetti is huffing and puffing with the exertion!
What is Slope?
Why is it such hard work? There’s a mathematical explanation! Slope!
Slope is a number that expresses the steepness of a line. Imagine you draw a line along the incline of the mountainside. Slope is the change in height compared to the change in width.
Formula for Slope
Let’s take a look at the formula for slope. M stands for slope, and the triangle symbol is the Greek letter delta, meaning change or difference.
To determine the slope of a line, select two points on a line then calculate delta y, the change of the y-values, to determine the change of height; divided by delta x, the change of the x-values, to determine the change of width.
When you determine the differences of the x- and y-values, make sure you maintain the order of the coordinates. Alternatively, you can think of this as rise divided by run or simply rise over run.
Slope Calculation Example 1 (Positive Slope)
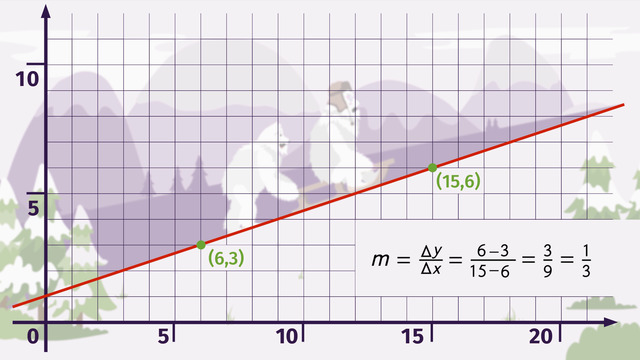
Let’s figure out the slope of the route where Leonetti is having such a tough time pushing his bride up the mountainside.
Draw a line along the side of the mountain's incline and select any two points on the line. Then determine the ordered pairs for both points, and plug the numbers into the slope formula.
6 − 3 = 3 and 15 − 6 = 9. You can simplify this fraction. So the slope is one over three, or one-third.
Slope Calculation Example 2 (Positive Slope)
What happens if the angle of the incline is different? Imagine Leonetti and Betty take a different route, this time less steep. It’s not such a workout for Leonetti to push Betty up the mountain. How does the slope differ?
Just like before, use the slope formula to divide the change in height by the change in width. One divided by five is equal to one-fifth. FYI, on the same line, regardless of where you select the two points, the slope will always be the same.
On the steeper route, the slope is 1/3 and on the less steep route, the slope is 1/5. So can we conclude, the larger the slope, the steeper the line? That is true for this situation, but the rule is: the larger the absolute value of the slope, the steeper the line.
Calculation example 3 (Negative Slope)
Both times Leonetti has pushed his wife up the mountain. Are you wondering what happens to the slope of the line when the Yetis sled down the mountain? Great question!
To model sledding down the mountain, let's put some new numbers into the slope formula. 2 − 6 = −4, and 15 − 3 = 12. Divide the numbers, and you get a slope equal to negative one third.
So, does that mean we can conclude that a negative slope means a line slanted down? You betcha! And, the greater the absolute value of the negative slope the steeper the line? Right again!
Calculation example 4 (No Slope)
Leonetti and his wife Betty are now on level ground. This time he pulls his wife across the snow. Again, she nags at him to go faster. What happens to the slope when there is no incline or decline?
Since there is no change in height, Y2 − Y1 = 0. X2 − X1 = 13. The slope is zero over 13 which is equal to zero. FYI again, if you draw another line parallel to this line… Guess what? The slopes will be the same!
Slope Tree
I have a fantastic graphic to help you remember all of this. No, it’s not a Christmas tree, it’s a slope tree!
- If the line slants up, the slope is positive.
- If the line slants down, the slope is negative.
- And, if the line is parallel to the x-axis, the slope is zero.
What about the tree trunk? What if the line is parallel to the y-axis? In that case, you would have a zero in the denominator, and we all know you can’t divide a number by zero – it’s not defined, so the slope is not defined as well.
What does all this mean for Leonetti and his nagging wife Betty?
Slope exercise
-
Label the picture using the correct terms.
HintsFor the line shown on the graph, the change in height and the change in width can be expressed in $3$ different ways.
If $\Delta y$ increases and $\Delta x$ stays the same, $m$ also increases.
Remember, slope is rise over run.
SolutionWe use the following formula to calculate the slope of a line:
$\text{slope}=\frac{\text{change in height}}{\text{change in width}}$.
Mathematically, we write this formula in the following manner:
$m=\frac{\Delta y}{\Delta x}$.
- $m$ stands for the slope
- $\Delta$ is the Greek capital letter delta, meaning 'change'
- $\Delta y$ or $\Delta x$ is the change in $y$ or $x$, respectively
- We can also expand $\Delta y$ to $y_2-y_1$, which is the difference between two y-coordinates. Similarly, $\Delta x$ can also be expanded to $x_2-x_1$, which is the difference between two x-coordinates
- Another way to think about $\Delta y$ is rise and another way to think about $\Delta x$ is run
- The pair of points, (x_1, y_1) and (x_2, y_2) is your choice. It also doesn't matter which is your "first" point and which is your "second" point; you just have to be consistent.
Point 1 "FIRST"
$\large m = \frac{20-25}{2-10} = \frac{-5}{-8} = \frac{5}{8}$
Point 2 "FIRST"
$\large m = \frac{25-20}{10-2} = \frac{5}{8}$
-
Determine the slope of the mountainside.
HintsPay attention to the order of subtraction:
It doesn't matter which point you choose as point $1$ or point $2$, but when finding the slope of a line, the order in which you subtract the numbers must be consistent.
The first coordinate of a point is the x-coordinate, and the second is the y-coordinate.
Remember, another way to remember slope is rise over run.
Reducing a fraction to its lowest terms means dividing the numerator and the denominator by the GCF.
SolutionWe use the formula $m=\frac{\Delta y}{\Delta x}$ to evaluate the slope, $m$.
- $\Delta y$ means change in height (or rise)
- $\Delta x$ means change in width (or run)
$m=\frac{6-3}{15-6}=\frac39=\frac13$
It's very important to pay attention to the order of subtraction. It doesn't matter which point you choose as point $1$ or point $2$, but when finding the slope of a line, the order in which you subtract the numbers has to be consistent.
-
Examine the slopes of the lines using the formula $m = \frac{\Delta y }{\Delta x}$.
HintsYou need to know two points on a line to calculate the slope.
For example $(0.5,2.5)$ and $(2.5,3)$ are two points on the violet line.
Lines that are parallel to the x-axis have a slope of zero because the y-coordinates of the two points are the same.
A rising line has a positive slope.
SolutionTo use the slope formula, we need two points from each line.
First, let's take a look at the blue line:
- The points are $(1,4.5)$ and $(3,0.5)$
- $m=\frac{0.5-4.5}{3-1}=-\frac42=-2$
- The points are $(0,3.5)$ and $(3,3.5)$
- we should have a zero slope since the y-coordinates of both points are the same
- $m=\frac{3.5-3.5}{3-0}=\frac03=0$
- The points are $(1,2)$ and $(4,5)$
- $m=\frac{5-2}{4-1}=\frac33=1$
- The points are $(0.5,2.5)$ and $(2.5,3)$
- $m=\frac{3-2.5}{2.5-0.5}=\frac{0.5}2=\frac14=0.25$
-
Determine the slopes of the different routes.
HintsThe larger the slope, the steeper the line.
Use the following formula to help you:
$\large{m=\frac{\Delta y}{\Delta x}}$
We only have positive slopes. Poor yetis!
Pay attention to the order of subtraction.
For example, for the following points:
$\large{(x_1,y_1)}$ and $\large{(x_2,y_2)}$
Though it doesn't matter which point is point 1 and which is point 2, you do have to be consistent.
$\large{m=\frac{y_2-y_1}{x_2-x_1}}$
SolutionFor each route, we use the formula:
$\large{m=\frac{\Delta y}{\Delta x}}$
Let's take a look at the slopes for the different routes.
Yellow Route:
- $m=\frac{4-2}{5-1}=\frac24=\frac12$
- $m=\frac{5-3}{4-2}=\frac22=1$
- $m=\frac{7-1}{4-1}=\frac63=2$
- $m=\frac{10-4}{3.5-2}=\frac6{1.5}=4$
-
Describe how the slope influences the look of a line in the coordinate plane.
HintsHave a look at two points lying on a line parallel to the x-axis, such as $(3,3)$ and $(5,3)$.
Use the equation $\large{m=\frac{\Delta y}{\Delta x}}$ to determine the slope of a line that passes through these points.
What's going on if you have a line parallel to the y-axis that passes through the points $(3,3)$ and $(3,5)$?
Use the equation $\large{m=\frac{\Delta y}{\Delta x}}$ to determine the slope.
Remember! Since you're not allowed to divide by zero, any slope that has zero in the denominator is undefined!
SolutionTake a look at the whole slope tree:
- on the left the line rises, so the slope is positive
- on the right the line falls, so the slope is negative
But what's going on with the tree trunk? A line parallel to the y-axis always indicates an undefined slope.
Hint: You can always tell a line will have an undefined slope if the $x$ coordinates of the two points are the same.
-
Calculate the height of the mountain.
HintsThe x-coordinate of the mountain peak is $15+20=35$.
The corresponding y-coordinate is the unknown height.
Use the formula $\large{m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}}$ and plug in all the known values.
In this case, $(x_2,y_2)$ are the coordinates of the mountain peak. The unknown value is $y_2$.
Isolate the unknown value by using opposite operations.
SolutionThe given information for this problem is:
- the slope ($m=2$)
- point on the mountain side ($15, 7$)
- x-coordinate of the mountain peak ($15 + 20, y_2$)
We need to use the formula $m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$ and plug in the known values:
$2=\frac{y_2-7}{35-15}=\frac{y_2-7}{20}$
Multiplying by $20$ we get the following equation:
$40=y_2-7$
Performing opposite operations, we add $7$ to both sides of the equation, giving us the solution:
$y_2=47$
The height of the mountain peak is 47 units tall.















Please consider different values for the points as the 6-3/15-6 looks as though you are subtracting the x-coordinate - y-coordinate.
Thank you for your kind comments! We're working hard to continue to bring you videos with easy-to-understand explanations...and fun stories!
I know, it's really good :)
really cool