Point-Slope Form
Basics on the topic Point-Slope Form
You are probably familiar with the formula for slope, you know, change in the y-values divided by the change in the x-values, the rise over the run. The point-slope form is simply the slope formula, rearranged.
The point-slope formula is the difference of the y-values set to equal the slope times the difference of the x-values. So, what’s the difference, and why do we need two formulas for the same thing? To solve equation of the line problems, the formula you use depends on what information is known and what you are amount you are solving for.
To use the slope formula, you know at least two points on a line and use this information to calculate the slope of the line. If you know the slope, and at least on point on the line, you can use the point-slope formula to calculate unknown ordered pairs on the line. Also, often your teacher will ask you to present an answer in a certain format. If you are asked to present the answer in point-slope form, you will want to be certain what that form looks like. Whatever equation of the line you decide to use, one thing is sure, you are going to love this video!
Use slope to create equations of the line.
CCSS.MATH.CONTENT.HSG.GPE.B.5
Transcript Point-Slope Form
A trio of busy business beavers gets together to make plans for the current year’s production of logs. Last year was problematic and they don't want to make the same mistake this year.
Last year, the beavers took a long vacation in the middle of the year and they had to work a lot of overtime just to reach their yearly goal. A member of the group has something to say about the plan, but the boss beaver won't let him speak.
The big boss goes on and on and on... The boss wants to plan for steady production throughout all twelve months. To figure this out, the beavers need some help calculating the equation of a line. Let's help them.
Point-slope Form and Slope Formula
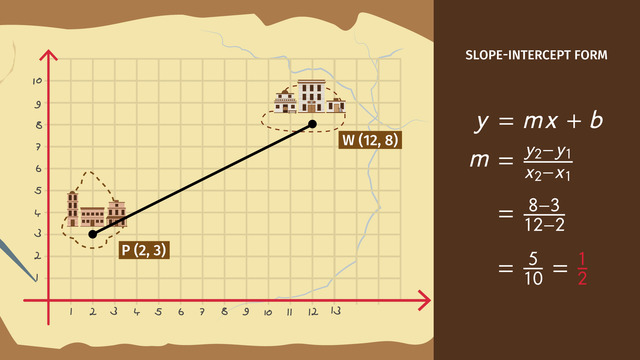
The beavers, and you, can use two equations to figure out a steady production plan: the point-slope form & slope formula. I'll write the formulas down.
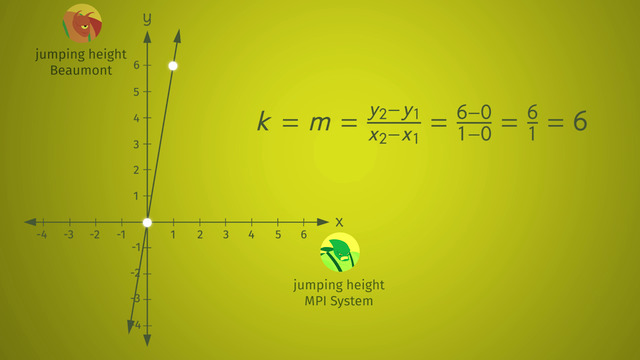
M stands for the slope of a line. Why M? No one knows for sure. What we do know is ordered pairs (x1, y1) and (x2, y2) are known points on the line, and the ordered pair (x, y) is any unknown point on the line.
Note how these two formulas are really just the same formula presented in two different ways. Why do we need to use two versions of the same formula? Well, stay tuned and you’ll see why two is better than one.
Point-slope Form Calculation 1
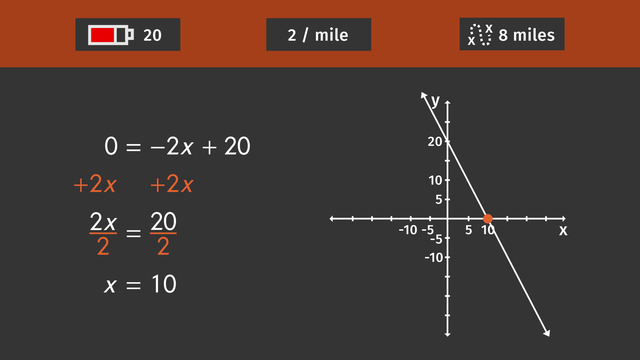
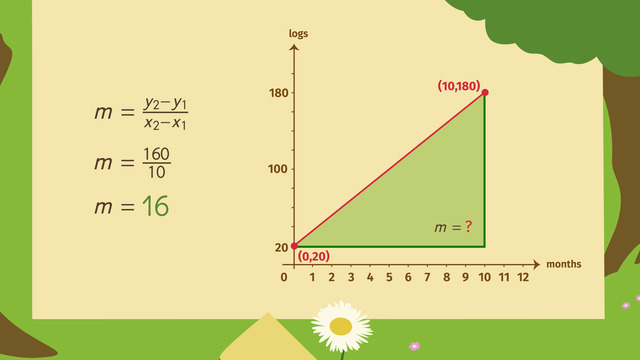
At the beginning of the year, the busy beavers have 20 logs in storage. To make sure they have enough logs for the annual winter festival, they need to have 180 logs in storage by the end of the tenth month.
Based on this steady production schedule, for each month, how many logs do the beavers need to produce and store?
To solve this problem, since we do know two points on the line, but we don't know the slope. The formula to determine the slope of the line is the best choice.
M is equal to difference of the two y-coordinates divided by the difference of the two x coordinates. Let's plug in the numbers.
The slope is equal to 180 minus 20 over 10 minus zero, that’s 160 over ten, which is equal to 16. To meet their production goal, they must produce 16 logs each and every month.
Point-slope Form Calculation 2
And, if they stay on this same production schedule, how many logs will they have in storage at the end of the twelve months?
Since we know the slope is equal to 16, and we know at least one point on the line, the point-slope form is easier to use to calculate the number of logs that will be produced and stored at the end of 12 months - if the beavers can stay on schedule, that is.
- Plug the numbers into the formula, y minus y1 is equal to the slope times the difference of x and x1.
- When we evaluate this, we get: Y is equal to two hundred twelve.
Awesome, problem solved! Check out the graph!
Now the beavers can get to work, to stay on schedule, they must produce 16 logs every month. That same member of the committee is still trying to speak, but the big boss only wants to listen to himself talk. I wonder what he wants to say.
Oh no! There’re no more trees! That must be what he was trying to say all along. I guess it's back to the drawing board...
Point-Slope Form exercise
-
Describe the point-slope form and the slope formula.
HintsThere's also the slope-intercept form:
$y=mx+b$, where
- $m$ is the slope and
- $b$ is the y-intercept.
The slope is the change in $y$ divided by the change in $x$.
Each point in the coordinate system is defined by the x-coordinate and the y-coordinate.
SolutionHere we have two different equations:
The point-slope form
$y-y_1=m(x-x_1)$
For this equation, we have to know one point $(x_1,y_1)$ on the line and the slope $m$.
The slope formula
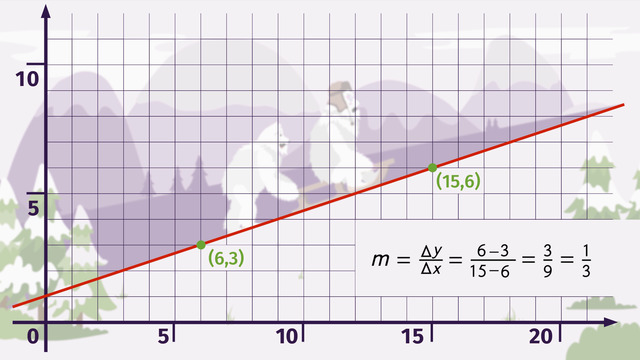
$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$
In order to use this formula, we have to know two points $(x_1,y_1)$ and $(x_2,y_2)$. Now we can calculate the slope by dividing the change in $y$ by the change in $x$.
-
Determine the slope of the equation.
HintsUse the correct order of subtraction.
The slope shows the increasing number of logs for each month starting with 20 logs in January.
SolutionFrom the given information, we know get two points:
- $(0,20)$ and
- $(10,180)$.
$m=\frac{y_2-y_1}{x_2-x_1}$.
Now we plug in the coordinates of the points. It's very important to be consistent with the order of subtraction:
$m=\frac{180-20}{10-0}=\frac{160}{10}=16$.
-
Determine the slope and the coordinates needed for the point-slope form.
HintsThe variable $x$ corresponds to the number of months. $y$ corresponds to the number of logs.
The slope is the increase of the number of logs over the number of months.
SolutionAt the beginning, $x_1=0$, there are 30 logs, $y_1=30$.
The beavers work 11 months, giving us a second x coordinate, $x_2=11$. The number of logs at this point, $y_2$, is unknown.
Each month they chop down 15 trees and produce 15 logs a month. This gives us the slope $m$.
Now we can write the equation:
$y-y_1=m(x-x_1)$
Let's plug in the values:
$y-30=15(x-0)=15x$.
After adding $30$ we can write the equation as $y=15x+30$.
If we plug $x_2=11$ into this equation, we get the amount of logs in November:
$y=15\times 11+30=195$.
Busy beavers!
-
Decide which equation corresponds to which line.
HintsThe points in the graph are
- $P(3,60)$,
- $Q(8,60)$
- $R(8,50)$
You can determine the slope by counting
- the number of steps to the right and
- the corresponding number of steps up or down.
All the slopes are positive.
Remember that the x-axis and the y-axis have different scales.
SolutionThe point-slope form is:
$y-y_1=m(x-x_1)$.
So we need:
- one point $(x_1,y_1)$
- the slope
- $P(3,60)$
- slope: one step to the right and twenty steps up $m=\frac{20}1=20$.
$y-60=20(x-3)$.
The green line
- $Q(8,60)$
- slope: two steps to the right and ten steps up $m=\frac{10}2=5$.
$y-60=5(x-8)$.
The blue line
- $Q(8,50)$
- slope: four steps to the right and ten steps up $m=\frac{10}4=\frac52$.
$y-50=\frac52(x-8)$.
-
Decide which equation is in point-slope form.
HintsIn order to solve the point-slope form we need:
- one point
- the slope.
Any point in the coordinate system has
- an x-coordinate and
- a y-coordinate.
The slope has to be multiplied by $x$.
There's also the slope-intercept form:
$y=mx+b$.
SolutionThe point-slope form can be solved with
- a point $(x_1,y_1)$ and
- the slope $m$.
-
Determine how many logs each beaver business has at the end of the year.
HintsWrite down the point-slope form for each business.
The point-slope form is:
$y-y_1=m(x-x_1)$.
The first coordinate of a point is the x-coordinate, the second is the y-coordinate.
One year later is represented by $x_2=12$.
SolutionWe can plug the values into the point-slope form
$y-y_1=m(x-x_1)$.
Justin's beaver business: $m=20$, $(0,35)$.
$y-35=20(x-0)=20x$.
After adding $35$ rewrite the equation as $y=20x+35$.
Now we plug in $x_2=12$ for one year:
$y=20\times 12+35=275$.
Paul*s beaver business: $m=15$, $(0,42)$.
$y-42=15(x-0)=15x$.
After adding $42$ rewrite the equation as $y=15x+42$.
Now we plug in $x_2=12$ for one year:
$y=15\times 12+42=222$.
Adele's beaver business: $m=25$, $(0,5)$.
$y-5=25(x-0)=25x$.
After adding $5$ rewrite the equation as $y=25x+5$.
Now we plug in $x_2=12$ for one year:
$y=25\times 12+5=305$.
Janet's beaver business: $m=18$, $(0,12)$.
$y-12=18(x-0)=18x$.
After adding $12$ rewrite the equation as $y=18x+12$.
Now we plug in $x_2=12$ for one year:
$y=18\times 12+12=228$.