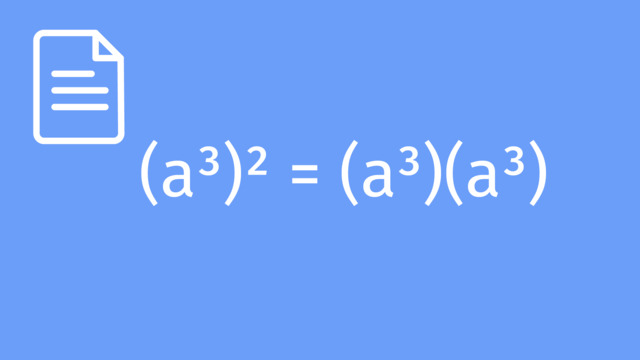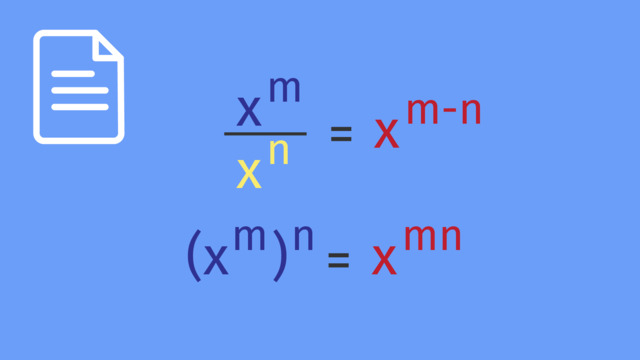Numbers in Exponential Form Raised to a Power


Basics on the topic Numbers in Exponential Form Raised to a Power
After this lesson you will be able to simplify exponential expressions involving powers of powers.
The lesson begins by teaching you the Powers of Powers Law. It leads to simplifying expressions with multiple terms using the Powers of Products Law. It concludes with simplifying expressions containing fractions using the Powers of Quotients Law.
Learn about numbers in exponential form raised to a power by helping Dr. MK keep the growth rate of her Grumples under control!
This video includes key concepts, notation, and vocabulary such as: power (a synonym for exponent); Powers of Powers Law (multiplying together the inner and outer exponents to simplify certain exponential expressions); Powers of Products Law (distributing an exponent over multiplication to simplify certain exponential expressions); and Powers of Quotients Law (distributing an exponent over division to simplify certain exponential expressions).
Before watching this video, you should already be familiar with the “repeated multiplication” rationale.
After watching this video, you will be prepared to learn about negative exponents in exponential expressions.
Common Core Standard(s) in focus: 8.EE.A.1 A video intended for math students in the 8th grade Recommended for students who are 13-14 years
Transcript Numbers in Exponential Form Raised to a Power
Midnight is approaching in Dr. Em Kay's laboratory. But what's this? Medical supplies? A dangerous chemical? Some new experiment? Oh, a Grumple! Isn't it cute? Dr. Em Kay decides to take the little one in. But one Grumple quickly turns to two, and two to four and more! Dr. Em Kay has got to get this under control, and fast. To figure out how many Grumples there'll be by morning, we're going to need to look at numbers in exponential form raised to a power. After a few hours of observation, Dr. Em Kay has come up with an expression for determining how many Grumples there are in her laboratory. g' cubed, raised to the fourth power where 'g' is the number of Grumples formed when a single Grumple reproduces. If you wanted to simplify this expression so that we just have one exponent, instead of two, where would you start? Well, we already know that 'g' cubed is the same as 'g' times 'g' times 'g'. Now to expand this even further, how can we write this expression without ANY exponents? Here, the exponent 4 is telling us that the expression in the parentheses is multiplied by itself 4 times. That gives us 'g' multiplied by itself 12 times which can be written as 'g' to the 12th power. If we compare this to our original expression notice that we get 12 by multiplying together the inner exponent 3 and the outer exponent 4. This is known as the Law of Powers of Powers. Any number 'x' raised to the 'm'th power, then raised to the nth power, equals 'x' to the power of 'm' times 'n'. Oh no! Some of the Grumples are getting into Dr. Em Kay's lunch! Now they're duplicating at a totally different rate! After four hours, the number of lunch-eating Grumples can be represented by this expression 7 times 'b', all raised to the fourth power where 'b' is the number of bites of human food consumed. Hm, how would you simplify this expression, so it is written without parentheses? Well, we know that the exponent 4 is telling us to multiply 7b by itself four times. Using the commutative property of multiplication we can group like terms together. Now, how would you simplify from here? Using exponential notation, we can write this as 7 to the fourth times 'b' to the fourth. Now compare that to the original expression. Notice anything interesting? We were able to distribute the exponent of 4 over the product of 7b. This is called the Powers of Products Law of exponents. It states that the quantity 'x' times 'y' all raised to the nth power is equal to 'x' to the 'n' times 'y' to the 'n'. Lets take a look at one more expression that Dr. Em Kay came up with to track the growth of the Grumples. The quantity 2 over 's', raised to the fourth power where 's' is the number of sleepy Grumples. What first step would you take if you wanted to simplify this expression? The exponent 4 tells us that we have to multiply the expression 2 over 's' by itself four times. From here we can group like terms to get the expression 2 to the fourth divided by 's' to the fourth. Once again, we can compare this to our original expression and see an example of the Powers of Quotients Law. Just like with multiplication, we can distribute exponents over division. Generally, this is written as 'x' over 'y' to the nth power is equal to 'x' to the 'n' over 'y' to the 'n'. Before we get back to those adorable Grumples, let's review. Three properties of exponents allow us to simplify expressions raised to a power. The Powers of Powers Law tells us we can multiply together the inner and outer exponents to simplify certain exponential expressions. The Powers of Products law allows us to distribute an exponent over multiplication. Similarly, the Powers of Quotients law allows us to distribute an exponent over division. Being able to simplify large expressions helps keep things under control which is good, because when working with exponents, things can get out of hand very quickly! Fortunately you can never have too many Grumples.