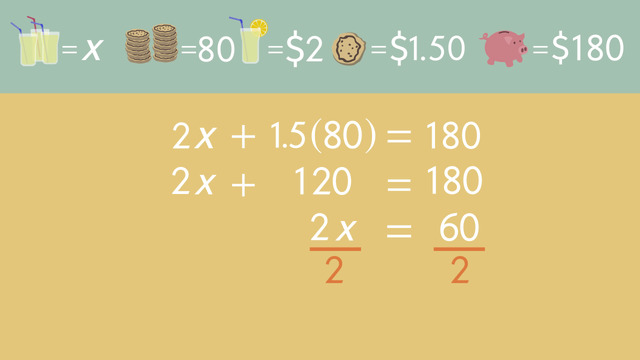Slope-Intercept Form

Basics on the topic Slope-Intercept Form
To write linear equations, there are three forms: slope-intercept form, point-slope form and standard from. For this video, we will investigate the very popular slope-intercept form.
Equations written in this form follow this format: y = mx + b. The m-value represents the slope which is the rise over the run of the line – the steepness of the line. The b-value represents the y-intercept, the point where the line touches the y-axis, and the x-coordinate is equal to zero. You can learn a lot from an equation of a line written in slope-intercept form.
Let’s look at an example: y = -2x + 5. From this linear equation, I can tell the line is sloping down because the m-value is a negative number. The slope is somewhat steep because the larger the m-value the more steep the line. I can also tell the line touches the y-axis at the ordered pair ( 0, 5).
That’s a lot of information from an equation with only three terms. No wonder teachers often tell their students to write equations of the line in slope-intercept form. To learn more about this form, and some practical uses in the real world, take a look at this video.
Use slope to create equations of the line. CCSS.MATH.CONTENT.HSG.GPE.B.5
Transcript Slope-Intercept Form
NASA is planning a special project for Valentine's Day--Mission4Love. They want to show a live sunset from Mars on national television.
In order to get the best view, they plan to send the Mars Rover to the top of a mountain. To complete the mission successfully, NASA has to figure out if the Rover has enough power to reach the top of the mountain and which route he has to take. We can help NASA by using slope-intercept form.
Introduction to Slope-Intercept Form & Formula
There are three common forms to write linear equations:
- Slope-Intercept form
- Point-Slope form
- Standard form
Today we will focus on Slope-Intercept form. As you can see, the slope is explicitly included in this form. Let's recall what slope is:
- Slope shows the steepness of a line.
- It can be calculated by "rise over run".
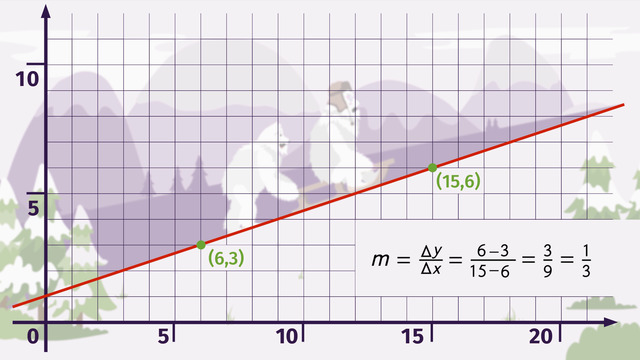
- If you take any two points on the line, you can calculate the slope using this formula: m equals the change of the two y-coordinates divided by the change of the two x-coordinates, or delta y over delta x for short. The Greek letter Delta means 'change' in math expressions.
So, what about about the intercepts? Let's look at the formula for the Slope-Intercept form. Remember, M represents the slope of the line, while b is the y-intercept.
Y-Intercept
Lets look at the graph of y=2x+1 in the coordinate plane.
The y-intercept is the point where the line crosses the y-axis. Here, the line crosses the y-axis at positive 1.
What happens if you change the y-intercept to 2? As you can see, the slope stays the same, but the whole line is shifted up one unit.
What happens if you change the y-intercept to -1? As you can see, the slope stays the same, but the whole line is shifted down by two units.
Slope
Now that we understand the concept of the y-intercept, let's look at slope.
Here, the slope is positive 2, meaning the graph is increasing from left to right. For every unit you go to the right, you must go up 2 units.
If we let m equal 1, the y-intercept stays the same, but now the slope is different. It still increases from left to right, but for every 1 unit you go to the right, you must also go up 1 unit.
If you change the slope to be zero, the y-intercept stays the same, but the line becomes horizontal. It is neither increasing nor decreasing.
Let's try changing the slope to −1. Again, the y-intercept stays the same, but the line is now decreasing from left to right because it has a negative slope. Now, for every unit right, you must go down one unit. Now that you've gotten the hang of slope-intercept form, let's get back to our Mars Rover.
Slope-Intercept Form Example 1
The Rover currently has 20 units of solar battery power left. If it uses 2 units of battery power per mile, how many miles can the Rover drive before it runs out of battery? Can it reach a spot that is 8 miles away?
Let's put this information into slope-intercept form:
- x represents the number of miles traveled by the rover.
- y represents the amount of battery power left. We need to find the numbers to replace m and b.
- The battery power decreases by 2 units each mile, so you should put −2 as the slope.
- Since the Rover starts with 20 units of battery power, 20 is the y-intercept.
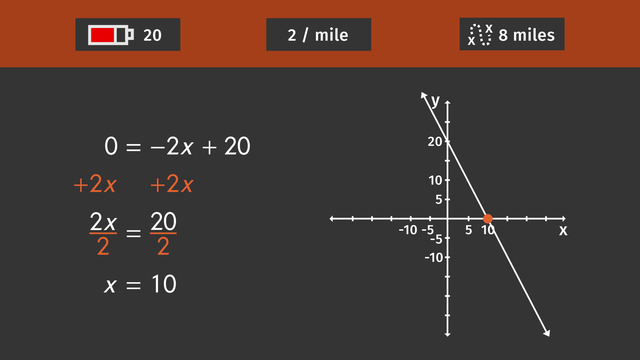
So how many miles can the Rover travel until the battery power gets down to 0 units? We put 0 in for y, the amount of battery power left. Now you can solve this equation to find x, the number of miles traveled:
- First, add 2x to both sides of the equation.
- Now you can divide both sides by 2.
And x = 10. So, this means that the rover can travel 10 more miles with it's power. It can easily reach the spot that is 8 miles away.
If you graph y = −2x + 20, you can see the solution right away: the x-intercept is 10. This is the point where now power is left.
Slope-Intercept Form Example 2
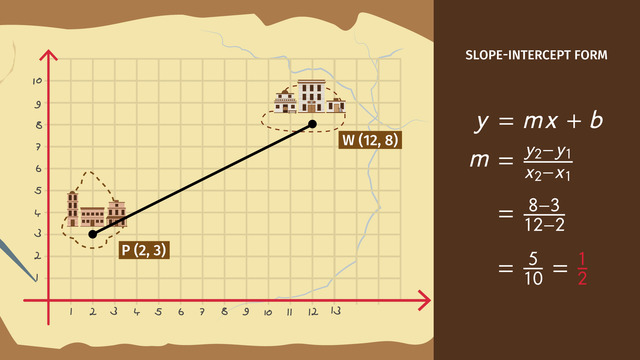
Let's look at one more problem. The Rover has to get to the top of the mountain to F (7, 6). It can either take a route starting here at S1 (1, 0) or here at S2 (5, 0). The rover can go a maximum slope of 2.5. Which route is better?
Since the Rover can't go over anything with a slope higher than 2.5, we need to find the slope of two different routes. First let's find the slope of S2(5, 0) to F(7, 6).
The slope formula is y2 − y1 over x2 − x1. So, the first slope is 6 − 0 over 7 − 5. This reduces to 6 over 2 which is 3. That slope is too steep! Hopefully the other starting point will be better.
The second slope from S1(1, 0) to F(7, 6). Is 6 − 0 over 7 − 1. This reduces to 6 over 6 which is 1. This slope is better for the Rover.
It looks like we are pretty much done. But unfortunately, the Rover needs the whole formula to get into perfect position for the sunset. To find the y-intercept, we can plug-in all of the other information we know.
The slope, m, is 1. Now we can choose a point (x, y) on the route to plug in values for x and y. Let's choose the final point (7, 6). 6 goes in for y. 7 goes in for x.
Now we can solve for b. Subtract 7 from both sides. B equals negative 1. So the equation for the Rover's route is y = x − 1.
NASA managed to get the Rover in the perfect position for a romantic sunset. But what is this? Love is in the air on planet Mars.
Slope-Intercept Form exercise
-
Describe the effects of changing $m$ or $b$.
HintsDraw the lines of
- $y=2x+2$ and
- $y=4x+2$
What can you see? If the slope changes, what happens?
The slope is:
$m=\frac{\Delta y}{\Delta x}$.
SolutionThe slope-intercept form is:
$y=mx+b$, where
- $m$ is the slope
- $b$ is the y-intercept.
- if $m$ is positive (negative), the line increases (decreases).
- if the absolute value of $m$ increases (decreases), the line is steeper (less steep).
- if $m=0$, the line is parallel to the x-axis.
- this is the point where the line crosses the y-axis.
- if $b$ increases (decreases), the line lies higher (lower) in the coordinate system.
-
Decide whether or not the Mars rover has enough battery power left to drive eight miles.
HintsThe slope-intercept form is:
$y=mx+b$, where
- $m$ is the slope
- $b$ is the y-intercept.
For each mile the rover travels the battery power decreases by 2 units.
Which means we'll have a negative slope.
The x-intercept is at $y=0$.
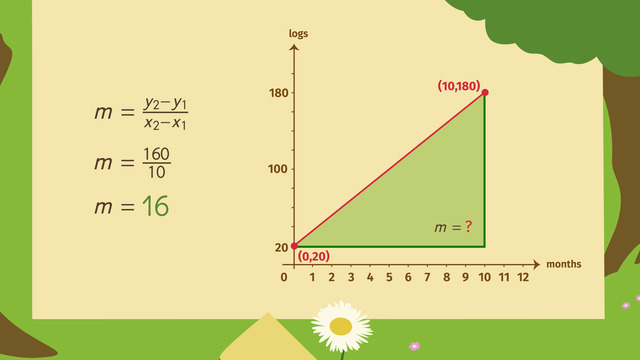
SolutionThe rover starts with 20 units of battery power left. This is the y-intercept. Because the rover needs two units of battery power each mile, the slope is $m=-2$. Each mile the battery power decreases by 2 units.
This gives us the equation: $y=-2x+20$.
We can determine the x-intercept of this equation:
$\begin{array}{rcr} 0&=&-2x+20\\ \color{#669900}{+2x} && \color{#669900}{+2x}\\ 2x&=&20. \end{array}$.
Now we divide by $2$ and get the x-intercept at: $x=10$.
Therefore, the Mars rover has enough battery power left to drive eight miles ($8<10$).
-
Determine the lines and corresponding equations.
HintsThe slope-intercept form is:
$y=mx+b$
- $m$ is the slope
- $b$ is the y-intercept.
First, have a look at the y-intercept.
For the slope, calculate the change in $y$ divided by the change in $x$.
$m=\frac{\Delta y}{\Delta x}$.
SolutionThe y-intercept of the blue, red. and violet lines is at $2$. The other two lines have the y-intercept at $4$.
Let's have a look at the slope:
- The blue line: for each four steps to the right, we go one step down - this gives us the slope $m=-\frac14$. This is the equation: $y=-\frac14x+2$.
- The yellow line is parallel to the blue line, so the lines have the same slope $m=-\frac14$. This is the equation: $y=-\frac14x+4$.
- The red line: for each two steps to the right, we go one step up - this gives us the slope $m=\frac12$. This is the equation: $y=\frac12x+2$.
- The green line is parallel to the red line. So the lines have the same slope $m=\frac12$. This is the equation: $y=\frac12x+4$.
- The violet line: for each step to the right we go one step up - this gives us the slope $m=\frac11=1$. This is the equation: $y=x+2$.
-
Determine the equations which the describe the Mars rover's expedition.
HintsTo write the slope-intercept form you need:
- the slope $m$ and
- the y-intercept $b$.
The slope is the change in $y$ divided by the change in $x$:
$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$.
Plug the x- and y-coordinates of the given points into the definition of $m$.
Pay attention to the order of subtraction.
For the intercept you can
- use the point-slope form
- substitute one point into the slope-intercept form
SolutionIf you'd like to write the slope-intercept form of an equation with the two points ($P(4,0)$ and $Q(9,-7)$):
- Calculate the slope by $m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$
- Determine the y-intercept with the slope.
$m=\frac{\Delta y}{\Delta x}=\frac{-7-0}{9-4}=-\frac75=-1.4$.
Now we can write down the equation as follows
$y=-1.4x+b$.
The y-intercept
We substitute $x$ and $y$ with the given coordinates of one of the two points. It doesn't matter which point we choose. With the point $P(4,0)$ - $x=4$ and $y=0$, we get the equation
$0=-1.4\times 4+b$.
This gives us $b=5.6$.
This leads to: $y=-1.4x+5.6$.
-
Decide which equations are in slope-intercept form.
HintsThe slope indicates the steepness of the line.
The y-intercept is the point where the line crosses the y-axis.
The point-slope-form is:
$y-y_1=m(x-x_1)$.
SolutionThe slope-intercept form is:
$y=mx+b$, where
- $m$ is the slope. The greater the absolute value of the slope, the steeper the line.
- $b$ is the y-intercept, the point where the line crosses the y-axis.
- $y=-2x+20$ and $y=2x+1$ are in slope-intercept form.
- $y-10=-2(x-5)$ is the point-slope form of $y=-2x+20$.
- $m=\frac{\Delta y}{\Delta x}$ is the slope.
-
Determine the correct equation for the given points.
Hints$\Delta y=y_2-y_1$ is the change in $y$, and $\Delta x=x_2-x_1$ is the change in $x$.
If the y-intercept is know, substitute the coordinates of any given point into the slope-intercept form to calculate the slope.
You can also check each the equation, do both points satisfy the equation?
Solution- First, we calculate the slope: $m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$
- Then, we determine the y-intercept.
- $m=\frac{\Delta y}{\Delta x}=\frac{4-2}{4-3}=\frac21=2$.
- Next we substitute the coordinates of, for example $Q$, in the equation $y=2x+b$. Rewrite the equation as $4=2\times 4+b$. Subtracting $8$ we get $b=-4$.
$\mathbf{P(1,-2)}$ and $\mathbf{Q(0,1)}$
- $m=\frac{\Delta y}{\Delta x}=\frac{1-(-2)}{0-1}=-\frac31=-3$.
- Next we substitute the coordinates of, for example $P$, in the equation $y=-3x+b$. Rewrite the equation as $-2=-3\times 1+b$. Adding $3$ we get $b=1$.
$\mathbf{P(4,6)}$ and $\mathbf{Q(2,5)}$
- $m=\frac{\Delta y}{\Delta x}=\frac{5-6}{2-4}=\frac12=0.5$.
- Next we substitute the coordinates of, for example $P$, in the equation $y=0.5x+b$. Rewrite the equation as $6=0.5\times 4+b$. Subtracting $2$ we get $b=4$.
$\mathbf{P(-6,0)}$ and $\mathbf{Q(3,-3)}$
- $m=\frac{\Delta y}{\Delta x}=\frac{-3-0}{3-(-6)}=-\frac39=-\frac13$.
- Next we substitute the coordinates of, for example $Q$, in the equation $y=-\frac13x+b$. Rewrite the equation as $-3=-\frac13\times 3+b$. Adding $1$ we get $b=-2$.