What are Parallel and Perpendicular Lines?


Basics on the topic What are Parallel and Perpendicular Lines?
Just to refresh your memory, parallel lines are lines that are the same distance apart, and perpendicular lines are lines that intersect at a right angle - which is the same as a 90 degree angle.
So we know what these lines look like on a graph, but how can we recognize equations of lines that are parallel or perpendicular? There is an easy answer for this question of parallel lines. The equations of parallel lines have slopes that are the same i.e. when written in slope-intercept form, the m-values of the lines will be the same.
How can we recognize equations of lines that are perpendicular? The answer to this question is not quite as easy as for parallel lines, so pay attention! The product of the slopes of perpendicular lines is equal to -1, meaning when the lines are written in slope-intercept form, the product of the m-values will be equal to -1.
So, just by looking at the equations, without plotting points on a graph and drawing a line, you can determine if the slopes are parallel or perpendicular? You sure can! To learn more about the slopes of parallel and perpendicular lines and see some awesome examples, tune in to this video.
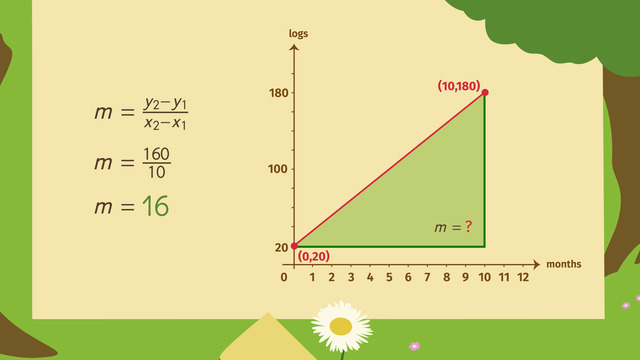
Write equations of the line.
CCSS.MATH.CONTENT.HSG.GPE.B.5
Transcript What are Parallel and Perpendicular Lines?
Although Richard the mage is the world's greatest wizard, he’s unhappy because he’s crazy jealous of his nemesis, The Dark Count.
Not only does The Dark Count have an incredible selection of the very finest English breakfast teas, he’s also a few inches taller than Richard.
To grow taller than his nemesis, Richard uses wizardry to create a special growth potion. But, The Dark Count has impressive magic skills plus knowledge of parallel and perpendicular lines, so anything could happen.
Parallel Lines
We’ll use our mad math skills to explain... The Dark Count is six feet tall. As he's a full grown man, the line to describe his height would look like this. The equation of this line is y = six.
Now for Richard the mage, he starts out at five feet tall and after drinking the potion, he'll grow quickly. We can describe the line of his growth as y = 1/4x + 5.
Compare the two lines. If all goes according to Richard's plan, you can see that after four days, Richard will be taller than The Dark Count. But The Dark Count, not to be outdone by Richard, drinks a growth potion as well.
The equation of the line describing the Count's height after he drinks the potion is y = 1/4x + 6. Look what happened to the graph. The lines are now parallel. Is it magic? No, just math.
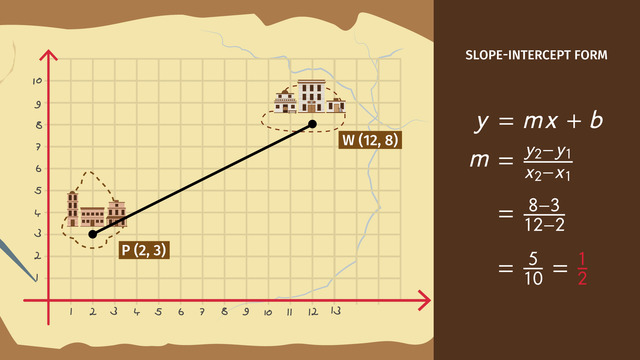
The equation of each line is in slope intercept form, y = mx + b. See? Both equations have a slope equal to one-fourth.
Whenever lines have the same slope, they are parallel.
Now, given this situation, Richard will never, ever be taller than his nemesis! Oh no, The Dark Count just donned his big sunday hat! Look! Now The Dark Count is 12 feet tall on day 12.
What would have been the equation for his height, if he had worn his hat from day 0? Remember, the slope of the equation shouldn't change since the slope is describing the same potion Richard and the Count used from before.
Basically, we are looking for the equation of the line that passes through point P AND is parallel to the line with the equation y = 1/4x + 6.
To solve, we can use the point-slope form. Substitute the values for point P into the formula as y1 and x1 then use the Distributive Property. Simplify the problem and display the answer in slope-intercept form. Notice the slopes of both lines are the same.
Perpendicular Lines
Richard the mage doesn't give up. He concocts a shrinking potion hidden inside an olive-eye and intends to slip it into The Dark Count's drink.
If this plan works, The Dark Count's growth will be described by this line. Its equation is y = −4x + 40.
Instead of growing one foot in four days, The Dark Count will shrink four feet in one day! Let's look at the graph. Something magical is happening.
The lines are no longer parallel; they are perpendicular. Do you see the ninety degree angle?
Again, it's math, not magic. The slopes aren't equal here, but they still have a special relationship. Can you figure it out? The slope of The Dark Count's growth line before was one-fourth and is now negative four. The product of the two slopes is negative one! The product of the slopes of two perpendicular lines is always negative one.
Let’s get back to the two magicians. Oh no! The Dark Count has pulled the ol' switcharoo on Richard.
What are Parallel and Perpendicular Lines? exercise
-
Describe the effect of the potions.
HintsThe general equation of a line is $y=mx+b$.
- $m$ is the slope
- $b$ the y-intercept
Lines with the same slope are either equal or parallel.
If the product of two slopes is equal to $-1$, the corresponding lines are perpendicular.
SolutionRichard the Mage is quite sad because his nemesis, the Dark Count, is taller than him.
- Richard the Mage: 5 ft. tall
- The Dark Count: 6 ft. tall
The equation that describes the Dark Count's height is $y=6$.
If the Dark Count drinks a magic growing potion as well, he will grow at the same rate as Richard the Mage. The equation describing the Dark Count's growth is $y=\frac14 x+6$. Since the slope of the lines describing Richard the Mage and the Dark Count's growths are now the same, we can say the lines are parallel.
Richard prepares a magic shrinking potion for the Dark Count. The equation to describe the growth after he will take the shrinking potion is $y=-4x+40$. If the lines are perpendicular, the product of the slopeswill equal $-1$.
$-4\times \frac14=-1$
Perpendicular means that two lines meet to form a right angle.
-
Determine the Dark Count's starting height without his Sunday hat.
HintsParallel lines have the same slope.
Each point has an x- and y-coordinate: $P(p_x,p_y)$.
The Distributive Property is:
$a\times(b+c)=a\times b+a\times c$
SolutionThe equation that describes the Dark Count's growth when he has on his Sunday hat is $y=\frac14x+b$. Remember, parallel lines have the same slope.
We still have to examine the y-intercept. This is the Dark Count's starting height including the Sunday hat, which is unknown. We know his height on Day $12$, $12$ feet. So $x=12$ and $y=12$.
We use the following point-slope-form:
$y-y_1=m(x-x_1)$
We substitute our known values, giving us:
$y-12=\frac14(x-12)$
Now we use the Distributive Property on the right side:
$y-12=\frac14x-3$
Adding $12$ on both sides give us the equation:
$y=\frac14x+9$
The Dark Count's starting height is our the y-intercept, 9 feet. So we also know the hat is 3 feet tall.
-
Examine which line corresponding to the equation is parallel or perpendicular to the given line.
HintsTwo parallel lines have the same slope.
Keep in mind that fractions can also be represented in decimal form.
If the product of the slopes of two equations is equal to $-1$, then the corresponding lines are perpendicular.
SolutionTake a look at the equation $y=\frac14x+6=0.25x+6$.
In order to decide if the equation of a line is parallel or perpendicular to a given line, you just have to look at the value for $m$.
- If $m=\frac14=0.25$, the corresponding lines are parallel
- If $m\times \frac14=-1$, the corresponding lines are perpendicular
- If neither is true, then the corresponding lines are neither parallel nor perpendicular.
- The lines corresponding to $y=\frac14x+7$ and $y=0.25x+9$ are parallel to the line $y=\frac14x+6$.
- The lines to $y=-4x+22$ and $y=-4x+43$ are perpendicular to the line $y=\frac14x+6$.
- The other two equations and their corresponding lines are neither parallel nor perpendicular to the line $y=\frac14x+6$ because one slope is $0.5$ and the other slope is $\frac13$. Our original equation has a slope of $\frac14$.
-
Determine the equation of a line that is perpendicular to the graph of the given equation.
HintsIsolate $4$ in the equation $m\times \frac14=-1$ to find the slope of a line that would be perpendicular to the line with slope $m=\frac14$.
Use the point-slope-form for linear equations, $y-y_1=m(x-x_1)$.
The equation we're looking for is in the form $y=mx+b$ where $m$ is the slope and $b$ is the y-intercept.
SolutionWe are looking for an equation $y=mx+b$ that is perpendicular to the line $y=\frac14 x+6$. What do we know?
- The slope of a line that is perpendicular to $y=\frac14x+6$ will have a slope that is the negative inverse of $\frac1/4$.
- The line passes through the point $P(7,14)$.
$\begin{array}{rcl} &~&\\ m\times\frac14&=&-1\\ \color{#669900}{\times 4} &&\color{#669900}{\times 4}\\ m&=&-4 \end{array}$
Now we use the point-slope-form $y-y_1=m(x-x_1)$ and substitute the known slope and the x- and y-coordinates of point $P$.
$y-14=-4(x-7)$
Next, we use the Distributive Property on the right side of the equation:
$y-14=-4x+28$
Finally, we add $14$ to both sides of the equal sign to get the equation into slope-intercept form.
$y=-4x+42$
-
Decide if each line is parallel or perpendicular to the red line.
HintsParallel lines have the same slope. Therefore, they have the same steepness.
The point where perpendicular lines meet forms a right angle.
There is only one line that is parallel to the red line and one line that is perpendicular to the red line.
SolutionThe red line belongs to the equation $y=\frac14x+5$.
The green line is parallel to the red line. The corresponding equation is $y=\frac14x +6$.
Notice that the slope of the two lines $m=\frac14$ is the same.
The slope of the blue line is $m=-4$. The product of this slope and the slope of the red line, $\frac14$, is $-1$. So the blue line is perpendicular to the red line. The point where perpendicular lines meet forms a right angle.
The orange and violet lines are neither parallel nor perpendicular to the red line.
-
Write equations to describe the new streets.
HintsIf the slopes of two lines are the same, they are parallel. If the product of the two slopes is $-1$, the lines are perpendicular.
Use the point-slope form for linear equations:
$y-y_1=m(x-x_1)$
$x_1$ and $y_1$ are the x- and y-coordinates of a given point.
Use the Distributive Property
$a\times (b+c)=a\times b+a\times c$
The equation we're looking for is given by $y=mx+b$.
- $m$ is the slope
- $b$ is the y-intercept
SolutionWe know the equation of one street is $y=2x+8$.
We want to know the equation of a parallel street.
- The slope is $m=2$ because the streets are parallel.
- Now that we know the slope and one point, $P(6,6)$, we can substitute the known values into the equation $y-y_1=m(x-x_1)$.
- $x-6=2(x-6)$
- Use the Distributive Property to get: $y-6=2x-12$
- Use Opposite Operations and add $6$ to both sides: $y=2x-6$
- The slope is the negative reciprocal of $m=2$, which is $m=-0.5$. To check our work, we multiply the two slopes to see if they equal $-1$. $-0.5\times 2=-1$.
- We're also given one point, $Q(1,10)$.
- Now we substitute the known values into $y-y_1=m(x-x_1)$ just like we did in the previous problem.
- $y-10=-0.5(x-1)$
- Use the Distributive Property to get $y-10=-0.5x+0.5$
- Use Opposite Operations and add $10$ to both sides: $y=-0.5x+10.5$