Direct Variation

Basics on the topic Direct Variation
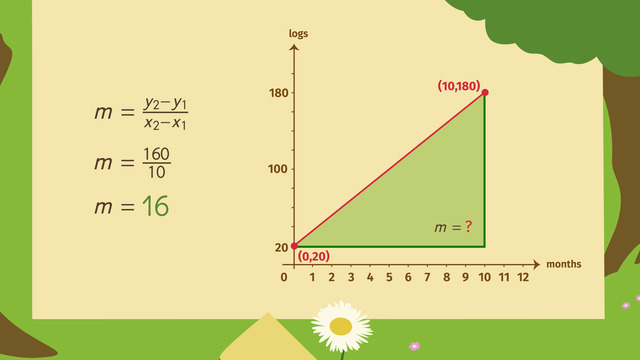
When variables are related by a constant, they have a direct variation. This constant is designated as the k-value, and we can write this relationship as a formula: y = kx or k = y/x.
As always, using algebra, you can solve for the unknown value by isolating the variable, so if you know two values of the equation, you can solve for the third. When variables have a direct variation, as one variable increases so will the other variable, at the same rate. Likewise, as the one variable decreases so will the other variable, also at the same rate.
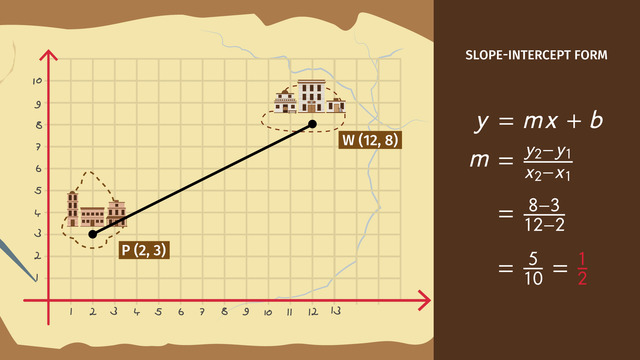
When you graph this relationship, you will notice the k-value determines the steepness of the line, just like the m-value in the slope-intercept form but with one major different. On the graphs of a line with a direct variation between the two values - the line always passes through the origin. If the line does not pass through the point ( 0, 0 ) then there is no direct variation and no constant of variation, k.
Understanding the topic of direct variation is especially important for real world use such as currency exchange. You wouldn’t want to get stranded in Tibet without enough Renminbi in your pocket just because you didn’t understand how to calculate the exchange rate with the dollar using the constant of variation. To see what I mean, watch this video.
Write equations of the line using slope.
CCSS.MATH.CONTENT.HSG.GPE.B.5
Transcript Direct Variation
Welcome to the Interstellar Olympics, three thousand five! Let the games begin! Let's join some of the top triathalon contestants... Sir Lift-a-Lot from Planet Broadray can lift three thousand pounds! And here’s another favored competitor, Schulzy from the MPI system. He can lift 2 pounds.
The Direct Variation
Sir Lift-a-Lot and Schulzy are currently tied. This is just incredible! What a competition! What? You don’t get it? How can they have tying scores? To help you understand, let’s explore Direct Variation. This means one value varies directly with the other.
In this case, the weight Sir Lift-a-Lot can lift is called y, and the weight Schulzy can lift is called x. We already said that Sir Lift-a-Lot and Schulzy are tied, but 3000 lbs is OBVIOUSLY larger than 2 lbs. So how can this be? The larger the planet, the greater the force of gravity is. This changes how much something weighs.
The constant of variation
The values are related by K, ......or the constant of variation. Now we can plug our known values into the Direct Variation formula. It doesn't matter which value is X and which is Y, but you do have to be consistent. Let’s assign two to X, and three thousand for Y. We divide both sides by 2 and get....
... K is equal to one thousand five hundred. Look what happens ...... when we double 3000 lbs to 6000 lbs. Notice thex value is also doubled. When variables have a direct variation, as one variable increases, so does the other. What do you think happens as one variable decreases? That's right, when we divide one value by four, the other decreases by a factor of four as well! Since k is our constant, it never changes.
Example
For example, while on their home planets, if Sir Lift-a-Lot were able to lift four thousand five hundred pounds, it would be the same as if Schulzy were to lift 3 pounds. To tie, for each additional 1,500 pounds Sir Lift-a-Lot lifts, Schulzy must lift one pound. Schulzy from the MPI system is also competing in the high jump. He can jump 1 foot. Wow! This alien has really brought his 'A' game!
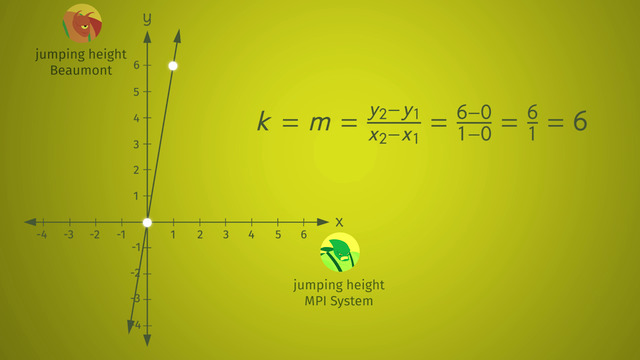
From Planet Beaumont, here's Schmiddy. Beaumont has less gravity, so although he ties with Schulzy, the absolute value of his jump is greater, measuring six feet. Let's draw a graph comparing the values of the jumps. Notice how the line goes through the origin? Graphs of values with a direct variation ALWAYS go through the origin. The y-intercept is always equal to zero.
The determine k
Take a look at another formula todetermine k, the constant of variation… Does this look familiar? You betcha. It’s the equation for slope of the line. So does that mean k is equal to the slope of a line? You betcha again! Let’s plug in the numbers for this situation and figure out the value for k. Do the math. K is equal to 6.
Weights and Measures
Now for the Meteorite Throw competition... Sir Lift-a-Lot from Planet Broadray has recorded a throw of 100 miles...and Schmiddy from Planet Beaumont has recorded a throw of 2 miles. To figure out which contestant is currently in the lead, the Interstellar Committee for Weights and Measures created this chart… Well, would you look at that! There is a direct variation because all of the k values are equal. We have another tie!
Sir Lift-a-Lot is up for his first throw of this Olympics. Oh boy! I think it's gonna be a good one! And there it goooooooooooes! That might be a new record! What's this? ...so THAT'S what happened to the dinosaurs!?
Direct Variation exercise
-
Draw the graph that represents the described direct variation.
HintsThe equation for direct variation is $y=kx$.
$k$ is the constant of variation and is also the slope.
$x$ represents the height reached by Schulzy, while $y$ represents the height reached by Schmiddy.
SolutionOn the planet MPI, Schulzy can jump $1$ ft, and on the planet Beaumont, Schmiddy can jump $6$ ft high.
The scores have a direct variation. So we can use the equation $y=kx$ to calculate the constant of variation k, or we can calculate the slope.
The slope of a line is defined by $m=\frac{y_2-y_1}{x_2-x_1}$.
- Schulzy jumps 1 ft and Schmiddy jumps 6 ft - this data is represented by the point $(1,6)$.
- If $x=0$, the direct variation gives us $y=0$. This is the point $(0,0)$, or the origin of the coordinate system. Lines formed by data that has direct variation always pass through the origin.
-
Determine the factor $k$.
HintsUse the equation $y=kx$ and substitute the given values for $x$ and $y$.
Solve this equation for $k$.
You can reduce a fraction by dividing the numerator as well as the denominator by the same number.
SolutionIn the equation $y=kx$, we can substitute each given pair of $x$ and $y$ and solve for $x$:
$\mathbf{x=100,~y=2}$
- This results in the equation: $2=k\times 100$
- Divide by $100$: $k=\frac2{100}=\frac{2\div2}{100\div2}=\frac1{50}$
- This results in the equation: $3=k\times 150$
- Divide by $150$: $k=\frac3{150}=\frac{3\div3}{150\div3}=\frac1{50}$
- This results in the equation: $4=k\times 200$
- Divide by $200$: $k=\frac4{200}=\frac{4\div4}{200\div4}=\frac1{50}$
This results in the equation $y=\frac1{50}x$.
-
Determine body weight on different planets.
Hints$y$ represents the body weight on the other planets.
$x$ represents the body weight of Susan or Johnny on the planet Earth.
The relationship between the weight on Earth and the weight on other planets varies directly, and the equation to calculate the constant of variation is: $y=kx$.
$100~lbs$ on Earth equals $140~lbs$ on Neptune.
SolutionTo calculate the constant of variation, use the equation: $y=kx$.
On Earth, $x$ is the given body weight of Susan, $140~lbs$, and $x$ is also the given body weight of Johnny, $174~lbs$. $k$ is the constant of variation.
We have to multiply $x$ by the constant of variation to get the body weight of Susan and Johnny on the different planets.
Jupiter, $\mathbf{k=2.63}$
- Susan: $y=2.63\times 140=368.2$
- Johnny: $y=2.63\times 174=457.62$
- Susan: $y=\frac1{1.15}\times 140 \approx 121.74$
- Johnny: $y=\frac1{1.15}\times 174 \approx 151.3$
- Susan: $y=1.4\times 140=196$
- Johnny: $y=1.4\times 174=243.6$
- Susan: $y=1.13\times 140=158.2$
- Johnny: $y=1.13\times 174=196.62$
- Susan: $y=2.63\times 140 \approx 53.23$
- Johnny: $y=2.63\times 174 \approx 66.16$
- Susan: $y=\frac1{2.9}\times 140 \approx 48.28$
- Johnny: $y=\frac1{2.9}\times 174=60$
-
Identify the equations.
HintsEach situation demonstrates a relationship that is directly variable.
The equation to describe a direct variation is: $y=kx$.
If you know to points on the line, you can use the slope formula to determine the constant of variation, $k$:
$\large k=m=\frac{y_2-y_1}{x_2-x_1}$
SolutionWhat do we know?
- Each situation is directly variable.
- The equation to describe a direct variation is: $y=kx$.
- We have to determine the constant of variation, $k$.
- We know the points $(2,2.4)$ and $(4,4.8)$.
- Therefore, we can find $k$ by using the slope formula $k=m=\frac{4.8-2.4}{4-2}=\frac{2.4}{2}=1.2$.
- $y=1.2x$.
- We know the two points $(3,96)$ and $(5,160)$.
- Therefore, we can find $k$ by using the slope formula $k=m=\frac{160-96}{5-3}=\frac{64}{2}=32$.
- $y=32x$.
- We know the two points $(2,12.8)$ and $(1.5,9.6)$.
- Therefore, we can find $k$ by using the slope formula $k=m=\frac{12.8-9.6}{2-1.5}=\frac{3.2}{0.5}=6.4$.
- $y=6.4x$.
-
Summarize the characteristics of direct variations.
HintsThe table at right shows a direct variation.
A linear equation in slope-intercept form is given by $y=mx+b$.
- $m$ is the slope
- $b$ is the y-intercept
For $y=mx+b$, if the variable $b$ is equal to $0$, there is a direct variation.
SolutionThe equation to solve for the constant of variation is: $y=kx$. When there is a direct variation, $b=0$ for $y=mx+b$. The graph of a direct variation always passes through the origin of a coordinate system and has a y-intercept of 0.
If you double the value for either variable, $x$ or $y$, the value of the other variable will double as well.
In a situation such as where the height of a jump depends on gravity, if Schmiddy jumps 6 ft while Schulzy jumps just 1 ft, we get the following values for the doubled height:
- $2\times 1= 2$ ft for Schmiddy
- $2\times 6=12$ ft for Schulzy
-
Find the equations that are represented by the graphs.
HintsTo solve for the constant of variation, k, you can use the formula: $y=kx$.
$k$ is the slope of the line. Keep in mind that the slope is rise over run.
The slope is given by the change in $y$ divided by the change in $x$.
SolutionEach line represents data that is directly variable and corresponds with the equation $y=kx$.
The light purple line
- passes through the point $(20,50)$
- therefore, $k=m=\frac{50-0}{20-0}=\frac{50}{20}=\frac52$
- the equation is $y=\frac52x$
- passes through the point $(30,50)$
- therefore, $k=m=\frac{50-0}{30-0}=\frac{50}{30}=\frac53$
- the equation is $y=\frac53x$
- passes through the point $(70,50)$
- therefore, $k=m=\frac{50-0}{70-0}=\frac{50}{70}=\frac57$
- the equation is $y=\frac57x$
- passes through the point $(50,50)$
- therefore, $k=m=\frac{50-0}{50-0}=\frac{50}{50}=1$
- the equation is $y=x$















my brother loves this video
my mom wont let me take notes :( but very fun!