What is Percent & Part of a Whole as a Percent
- Understanding Percent as a Part of a Whole
- Understanding Percent as a Part of a Whole – Explanation
- Understanding Percent as a Part of a Whole – Example
- Understanding Percent as a Part of a Whole – Practice
- What is Percent & Part of a Whole as a Percent – Summary
- What is Percent & Part of a Whole as a Percent – Frequently Asked Questions


Basics on the topic What is Percent & Part of a Whole as a Percent
Understanding Percent as a Part of a Whole
A percent is a unit of measurement used in mathematics to express how a number relates to 100. It is crucial in everyday life, helping us understand everything from financial discounts to statistical data and more.
Percent: A percent is written with the symbol % and represents a part of a whole divided into 100 equal parts.
Understanding Percent as a Part of a Whole – Explanation
Percentages are a fundamental concept in expressing proportions and ratios. They provide a clear, standardized way to compare different quantities and measure parts of a whole.
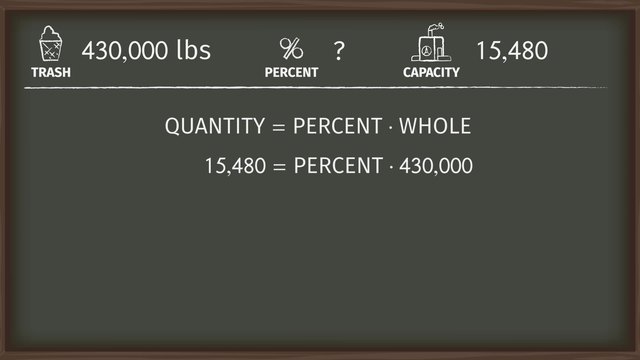
The relationship between a part, the whole, and the percent can be expressed with the proportion:
$\frac{\text{Percent}}{100} = \frac{\text{Part}}{\text{Whole}}$
Understanding Percent as a Part of a Whole – Example
To fully grasp how percents relate to parts of a whole, let’s look at a practical example:
Example 1: Imagine a garden that is divided into 4 equal sections. If 1 section is planted with flowers, what percent of the garden is used for flowers?
Example 2: A parking lot has 50 spaces, and 15 of them are occupied by cars. What percent of the parking lot is currently used?
Example 3: A small tank can hold 20 liters of water, but currently, it has 12 liters. What percent of the tank is full?
Understanding Percent as a Part of a Whole – Practice
Now take some time to try some of these on your own!
What is Percent & Part of a Whole as a Percent – Summary
Key Learnings from this Text:
- Percentages represent a ratio or proportion expressed as a fraction of 100.
- Understanding how to calculate percentages from a fraction of a whole allows for clearer, more applicable insights in both academic and real-world scenarios.
- The formula $\frac{\text{Percent}}{100} = \frac{\text{Part}}{\text{Whole}}$ is essential for solving many percent word problems involving ratios and proportions.
Here you will see some common part and whole ratios and their percentages.
| Part | Whole | Percent |
|---|---|---|
| 1 | 2 | 50% |
| 1 | 3 | 33.33% |
| 1 | 4 | 25% |
| 1 | 5 | 20% |
| 1 | 6 | 16.67% |
| 1 | 8 | 12.5% |
| 1 | 10 | 10% |
| 2 | 5 | 40% |
What is Percent & Part of a Whole as a Percent – Frequently Asked Questions
Transcript What is Percent & Part of a Whole as a Percent
Leelee is an ambitious young entrepreneur who's always got her finger on the pulse of the latest online trends. Today she’s launching a crowdfunding campaign to start her new high-end fashion line for pets. Raising money online is about as easy as herding cats. So to track her fundraising, we're going to have to help Leelee calculate percent as part of a whole. Leelee starts her fundraising efforts by blasting out an email to 135 people she knows. She hopes that 40% of them will respond. So how many people is that? We can create a diagram to help us visualize 40 percent of 135. Let's first look at the WHOLE, or 100 percent of the people she emailed. What number of people represents our whole? Since Leelee emailed a total of 135 people, that will represent 100 percent. Now, we want to figure out how many people represent our PART of 40 percent, so let's mark that here on the diagram. How can we go from 100 percent to 40 percent? One strategy for answering this question is to figure out what 1 percent is, then use that information to calculate 40 percent. So if we know that 135 people is equal to 100 percent, how could we find how many people are equal to 1 percent? Notice we can divide our whole of 100 percent by 100 to get 1 percent, so we can also divide our whole of 135 by 100 to find the missing part. That means 1.35 people is equal to 1%. Now that we know what 1 percent is, how do you think we can figure out 40 percent? Since we can multiply 1 percent by 40 to get 40 percent, we can also multiply 1.35 people by 40 to get 54 people, which represents 40% of the WHOLE. With 54 friends ready to donate, Leelee is feeling as excited as a puppy at a dog park. On the crowdfunding site Leelee is using, she needs to declare a fundraising goal. In order to collect the money she raises, she needs to reach 65% of that goal. Leelee needs at LEAST 19 hundred and 50 dollars to get her clothes on the catwalk. So she needs to set a HIGHER fundraising goal. If 19 hundred and 50 is ONLY 65% of her goal, what should her goal be? Let's use a diagram again, to help us sort all of that information out. We want to figure out our whole, which is a dollar amount equal to 100 percent of Leelee's goal. So let's call that 'x' on the diagram. Now, where on the diagram do we put our PART, which is 65 percent and 19 hundred 50? We know that 19 hundred and 50 is 65% of her goal. So we have the PART and the PERCENT. We know that the part equals the percent TIMES the whole. So 19 hundred and 50 is 65% times 'x'. Since 65% is 65 hundredths, how can we isolate ‘x’ to solve our equation? We can start by getting rid of the fraction on the right side of the equation by multiplying both sides by its reciprocal, 100 over 65. Then, we just simplify. So 3000 is equal to 'x'. That means Leelee needs to set a WHOLE fundraising goal of 3000 dollars. Let's see how her fundraising is going so far. Check it out: she just got a 900 dollar donation from some anonymous fat cat! Starting with this 900 dollars, what percent has Leelee raised so far, and what percent is left for her to meet her goal? The diagram shows us that 900 dollars gets her PART of the way to the WHOLE of 3000. Let’s call the unknown PERCENT ‘p’. Now let’s use our handy equation, part equals percent times whole. Since we're solving for the percent 'p', we can rewrite that as part over whole equals the percent. Plugging in our known values for PART and WHOLE, we can simplify our fraction to get 9 over 30 or 3 tenths, which we can rewrite as a decimal. We can write this as our needed percent because thirty one-hundredths is equal to 30 percent. Now we can see that Leelee has raised 30 percent of her goal. That means she has 70% left to go. Before Leelee's grand opening, let’s review the tools we used to calculate percents, using parts and wholes. First, creating a diagram is a great way to visualize the relationship between percent, part, and whole. When we know a value and its percent, we can convert to 1% by dividing by 100, then expand in order to find the value for a desired percent. We also have an equation, part equals percent times whole, which we can always use to substitute and solve for any unknown value. With a couple more deep-pocketed donations, Leelee has launched her pop star fashion for domesticated animals! But what’s wrong Leelee? Tired of internet fame already? Yikes! Or should I say... Mee-YOW!
What is Percent & Part of a Whole as a Percent exercise
-
Find the percent of the total.
HintsRemember, to find the percent of a total, you need to solve the equation: $\frac{\text{Part}}{\text{Whole}}$ = Percent
The part is 350 and the whole is 1,000. You need to solve the equation $\frac{350}{1,000}$ = Percent
Once you solve $\frac{350}{1,000}$, you need to multiply the result by 100 to get the percent
Solution$\frac{\text{Part}}{\text{Whole}}$ = Percent
$\frac{350}{1,000}$ = Percent
$0.35$ = Percent
$0.35\cdot100$ = Percent
$\bf35%$ = Percent
-
Find the percent donated.
HintsThe part is $\$750$ because this is only a piece of the total donated money, while $\$5,000$ is the goal so this is the whole.
If you divide the part by the whole, you must multiply the decimal product by 100 to get the percent.
Solution$\frac{\text{Part}}{\text{Whole}}$ = Percent
Which value is the part? 750 Which value is whole? 5,000 Therefore, our equation is: $\frac{\textbf{750}}{5,000}$ = Percent
Divide 750 by 5,000 to find the percent. 0.15 = Percent
Now multiply to find the percent. $0.15\:\cdot$ 100 = Percent
15% = Percent
-
Find the number of respondents.
Hints135 is the total, which is 100% of people.
Remember, what you do to one side, you must do to the other side too. This means if you divide one side by 100, you must divide the other side by 100 too.
Solution81 people responded to the invitation.
-
Find 100% of the total.
HintsFirst set up an equation for: Part = Percent $\cdot$ Whole
When you set up the equation with the values, it should look like this:
$2000=\dfrac{40}{100}\cdot{x}$
We can solve the equation by multiplying both sides by the reciprocal fraction to isolate $x$.
The reciprocal of $\dfrac{40}{100}$ is $\dfrac{100}{40}$, which must be added to both sides of the equation.
After isolating $x$, the equation should now read:
$\dfrac{100}{40}$ * 2,000 = $x$
SolutionPart = percent $\cdot$ whole
$2,000$ = $\dfrac{40}{100}$ $\cdot$ $x$
$\dfrac{100}{40}$ $\cdot$ $2,000$ = $\dfrac{100}{40}$ $\cdot$ $\dfrac{40}{100}$ $\cdot$ $x$
$\dfrac{100}{40}$ $\cdot$ $2,000$ = $x$
$2.5$ $\cdot$ $2,000$ = $x$
$\$$$5,000$ = $x$
-
Find the number of respondents.
HintsFirst set up a table to help solve the problem.
With your table set up, find what 1% of the people and percent is. To do this, think about what you need to divide 100% by to get 1%, and do the same for the people column.
1% of people is 1.5. You need to multiply 1.5 by 30 to find 30% of the people.
SolutionFirst divide the total number of people, 150 by 100 and 100% by 100.
This gives us 1.5 people and 1%.
Then multiply what 1% of people is by 30, to get 30% of people.
Next, do the same to the number of people: $1.5 \cdot 30$.
$1.5 \cdot 30$ = 45 people.
-
Find the goal total.
HintsWhen finding the part, both the percent and whole are important.
The formula Part = percent $\cdot$ whole can help.
The current amount raised can help you find the goal total.
Remember, $\frac{100}{70}$ $\cdot$ $\frac{70}{100}$ cancels itself out by cross multiplication.
$\frac{100}{70}$ is asking you to solve 100 divided by 70, and then multiply this value by the total raised so far.
SolutionPart = percent $\cdot$ whole
$\frac{100}{70}$ $\cdot$ __USD__4,900 = $\frac{100}{70}$ $\cdot$ $\frac{70}{100}$ $*$ $x$
$\frac{100}{70}$ $\cdot$ __USD__4,900 = $x$
__USD__7,000 = $x$
The goal total is __USD__7,000