A Fraction as a Percent
Basics on the topic A Fraction as a Percent
Fraction as a Percent – Definition
Understanding how to convert between fractions and percentages is an essential skill in mathematics and everyday life. Whether you're working out discounts, analyzing data, or comparing statistics, knowing how to switch between these formats can provide clearer insights and more accurate calculations. Further, explore this concept with What is Percent & Part of a Whole as a Percent and see how these ideas apply in various scenarios in Applying Percentages to the Real World.
Fraction: A mathematical expression representing a part of a whole, denoted as $\frac{\text{numerator}}{\text{denominator}}$.Percent: A way of expressing a number as a part of 100, denoted by the symbol %.
Fraction as a Percent – Explanation
Converting a fraction to a percent involves a simple multiplication by 100, as you are converting a part out of one whole into a part out of one hundred. Conversely, converting a percent back into a fraction involves dividing by 100 and simplifying if necessary.
Converting a Fraction to a Percent
Imagine you have completed $\frac{3}{4}$ of a project. To find out what percent of the project is complete, you would convert the fraction to a percent.
Try some more like this on your own!
Concerting a Percent to a Fraction
If a survey shows that 25% of people prefer reading to other hobbies, we can convert this percent into a fraction to simplify data analysis.
Practice converting percent to a fraction.
Converting Between Fraction and Percent
| Conversion Type | Formula | Example |
|---|---|---|
| Fraction to Percent | $\left(\frac{N}{D}\right) \times 100$ | $\frac{1}{2} \rightarrow 50\%$ |
| Percent to Fraction | $\frac{Percent}{100}$ | $50\% \rightarrow \frac{1}{2}$ |
Fraction as a Percent – Summary
Key Learnings from this Text:
Understanding how to convert between fractions and percentages is crucial for practical applications in real-life scenarios.
The formulas for converting from a fraction to a percent and vice versa are straightforward but essential for accurate data representation.
Fraction as a Percent – Frequently Asked Questions
Transcript A Fraction as a Percent
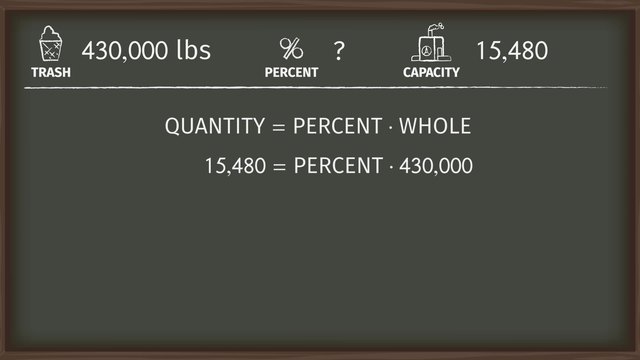
Olivia has spent the last months training herself physically and mentally to be ready to battle wildfires. She’s passed every test so far and now she’s reached the last challenge. The firefighters have set a controlled burn in a field at their training center and she must extinguish 85% of the flames, by herself, before sundown. In order to track her progress and accomplish the mission, Olivia will need to convert fractions to percents, and back again. Time is ticking but before grabbing a firehose, Olivia needs to perform some calculations. The whole field is divided into 20 squares. If she needs to extinguish 85% of the field, how many squares IS that? Remember, a percent is a quantity out of 100. That means 85% is the same as the fraction 85 over 100. We can use equivalent fractions to rewrite 85 over 100 to what we need. For this problem, we want to find the equivalent fraction that has 20 in the denominator. 85 over 100 equals WHAT over 20? In order to change the denominator from 100 to 20, we need to divide by 5. But since we want an equivalent fraction, we also have to divide the numerator by 5. Dividing 85 by 5 gives us 17 which tells us 85 percent is equivalent to the fraction seventeen twentieths. Olivia needs to extinguish 17 out of the 20 squares. After a few hours of hard work, she takes a short break giving us time to calculate her progress so far. Olivia has extinguished the fire in 8 squares out of 20. What percentage has she extinguished so far? Let's take a look at the grid. Here are the eight squares where the fire has already been extinguished. On the right side we can write the number of squares in each row: 4, 8, 12, 16 and 20. Hmm, this reminds us of a double number line, so let's put the strip right here and turn it on it's side. The whole is always equal to 100 percent, so we can write that 20 squares is equal to 100 percent. We need to divide the 100 percent into 5 parts. Since 100 divided by 5 is 20, each part is 20 percent. That gives us 20 percent, 40 percent, 60 percent, and 80 percent. Looking at the double number line, that shows us that 8 squares represents 40 percent. That's 40 percent of the fire already extinguished. Olivia just remembered that she can earn a special commendation if she extinguishes at least 90 percent of the field before noon and now that seems like a real possibility. It looks like Olivia has extinguished all the squares but one! Has she earned the special commendation? What is the fraction of the fire that is still burning? One twentieth. What percent is that? Again, a percent is a quantity out of 100. That means we have to find an equivalent fraction with 100 in the denominator. What can we multiply 20 by to get 100? 100 divided by 20 is 5, so we need to multiply the denominator by 5. But since we want to find an equivalent fraction, we also have to multiply the numerator by 5. That gives us 5 over 100, which is equal to 5%. If only 5% is still burning, what percent did Olivia extinguish? 100%, which represents one whole, minus 5% gives us 95%. She did it! While Olivia takes a well-earned rest, let's review. Because percents are a quantity out of 100, we can convert fractions to percents, and vice versa. To convert a percent to a fraction, first write the percent as a fraction with 100 in the denominator. Then multiply or divide the numerator and denominator by the same number to find the equivalent fraction with the denominator you want. To convert a fraction to a percent, we first find what number we need to multiply or divide the denominator by in order to get 100. Then we multiply or divided both the numerator and denominator by that value to get a fraction out of 100. The numerator shows us the percent. This allows us to compare numbers even when they are given in different forms. Congratulations Olivia! With careful conversions of fractions to percents and back, you'll always be able to track your firefighting progress. But what’s this? Hmm, I’m not sure fractions and percents will help here. Olivia has to rescue 100% of the cat!
A Fraction as a Percent exercise
-
What is the correct order of steps to convert a fraction to a percent?
HintsWe always start off by setting up our tape diagram with 0%, 100% and the total parts that make up 100%.
How many parts do we need to divide the diagram into?
How many parts do we need to shade?
What does the shaded part represent?
SolutionSet up a tape diagram, marking 0%, 100% at the top, and 0 and the whole underneath. In this example, the whole would be 2.
Now divide the tape diagram by the number of the whole provided. Here, we would divide it into two parts. We notice this is halfway, so mark 50% at the top.
Next, shade in how many parts of the whole the fraction has. The fraction in the example has one part of the whole, so shade in one part.
Finally, write the percent as shown by the number of parts shaded in. In this example, 1 part of 2 is equal to 50%. This means $\frac{1}{2}$ = 50%.
-
Understanding the importance of fractions and percent.
HintsRemember that fractions show how many parts of a whole there is.
The same is true with percentages!
$\frac{3}{5}$ and $\frac{60}{100}$, or 60%, are linked. With this information, how many parts out of 5 does 60% represent?
SolutionA percent represents a part of something out of 100. When converting a fraction to a percent, it tells us how many parts out of 100 the fraction represents.
For example, $\frac{3}{5}$ as 60% means that 3 out of every 5 parts make up 60% of the whole. This helps us understand the fraction's relationship to a whole hundred.
-
Which answer shows $\frac{2}{8}$ as a percent?
HintsRemember, set up a tape diagram to help.
Find what 25%, 50%, and 75% would be on the tape diagram.
SolutionIf we shade in one part of the tape diagram up to $\frac{2}{8}$, we see that it is equal to 25%.
This means $\bf{\frac{2}{8}}$ as a percent is 25%.
-
What percentage are these fractions equal to?
HintsRemember to set up tape diagrams like this one for $\frac{1}{2}$ to help you.
Then shade in 1 part. $\frac{1}{2}$ is equal to 50%.
SolutionHere we can see the correct pairs.
-
Which answer represents the displayed fraction as a percent?
HintsSet up a tape diagram like this to help you.
Divide 100 by 10, to get 10. Each block is worth 10%.
Now shade in the total parts of the fire Olivia put out, which is 8.
SolutionWith the tape diagram set up, shade in 8 parts, since each block represents 1 part.
Now look at the matching % at the top.
We can see that $\bf{\frac{8}{10}}$ is equal to 80%.
-
Enter the values that make this step by step solution true.
HintsRemember that the numerator represents the parts of the whole, and the denominator represents total parts that make up the whole.
What must you multiply the denominator, 20, by to get 100? You need to multiply the numerator by the same value.
SolutionFirst, we find out how much of the fire remains. 5 parts of the fire remain, so this is our numerator. The denominator is represented by how many parts in the whole. Here, it is 20, so our fraction is $\frac{5}{20}$.
Next, we need to create a fraction with 100 as the denominator. To do this, we multiply 20 by 5 to get 100. We must multiply the numerator by the same value; 5 multiplied by 5 is 25. The new fraction is $\frac{25}{100}$.
Finally, we can convert $\frac{25}{100}$ to a percent. A percent represents out of 100, so $\frac{25}{100}$ as a percent is 25%. This means that 25% of the fire remains.


















its alright ig