Comparing Quantities with Percent

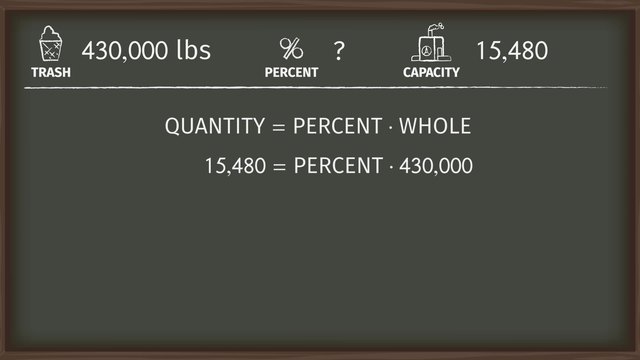
Maryam likes to spend her afternoons outside, dreaming up creative ways to make the world a better place. One day, while sitting outside as usual, an idea suddenly pops into her head! She realizes that she could combine a plastics recycling machine WITH a 3-D printer. Then almost all of her town’s waste could be turned into useful products. In order to make her project work, Maryam will have to recycle a high percentage of her town’s trash. Determining how much trash she can recycle AND the number of machines she needs, will require Comparing Quantities with Percents. Maryam does some research and discovers that her town produces 430,000 pounds of trash every day. Her research further shows that 72% of that garbage is recyclable. So how many pounds of trash will her machines need to digest every day? Remember that a percent is a ratio of the part to the whole. We want to find 72% of 430,000 pounds. Therefore the ratio of part to whole is 72 over 100. The whole amount of trash produced is 430,000 pounds. We are looking for the recyclable PART. To solve, let’s first simplify 72 over 100. To divide 72 by 100, we just move the decimal to the left two places. So 72 over 100 is zero point 72. That’s how we write 72% in DECIMAL form. Now we just isolate the variable 'Part'. Multiplying both sides of the equation by 430,000 gives us that the 'PART' equals point 72 times 430,000. Before completing this calculation, note that we can skip DIRECTLY to this final step to solve an equation involving percents. We can always write the PART as the PERCENT times the WHOLE, where the percent here is written as a decimal. Since the PART is the QUANTITY of the WHOLE we are interested in, let's call the part QUANTITY from now on. And the whole is always here. So in general, we can find desired QUANTITIES using the equation QUANTITY equals PERCENT times WHOLE. This shortcut avoids the step of writing a proportion, and we’ll use it often. So, what IS the recyclable quantity here? The QUANTITY equals 309,600 pounds. Maryam is a careful scientist, so she’ll check her result using a 10 by 10 grid. Let's start again. We want to find 72% of 430,000 pounds of trash. The WHOLE 430,000 pound grid is divided into 100 squares, so how much trash does ONE square represent? 430,000 pounds divided by 100 squares gives us 4,300 pounds of trash per square. That's 1% of the trash. We can find 72% by multiplying 4,300 times 72. That gives us 309,600 pounds of recyclable materials each day. The same result Maryam got previously. It’s a lot of trash to recycle, so Maryam will need to build her machines to maximize the amount of garbage they can process. Maryam has already built a few 3-D printers, but she needs to perform some calculations to see how many her town needs. Maryam decides to solve this problem by comparing percents. So first, she wants to find the percent of the town’s trash that each machine can handle. In her tests, Maryam discovered that each machine can process 15,480 pounds of trash per day. And we already know that the whole town produces 430,000 pounds of trash per day. Let’s use our equation, QUANTITY equals PERCENT times WHOLE. What is our quantity? It's the amount that each machine can process per day, 15,480 pounds. And what is the whole? 430,000 pounds. We can solve for the PERCENT by dividing 15,480 by 430,000. We get that PERCENT equals point oh five. We can rewrite this decimal as a PART over a 100 by moving the decimal two places to the right. So each machine can process 5% of the town’s trash every day. So how many machines are needed to recycle 72%? We can use our 10 by 10 grid again to visualize this problem. The 100 squares in our grid together represent 100% of our trash. 72 squares represent the 72 % of the trash that is recyclable. Since one square represents 1% of the town's trash, and one machine can process 5% of the trash, each machine's capicity is represented by 5 squares. So we need one, two, three, four, five. 14 doesn't quite do it. It looks like we need 15 machines to process all of the town's recyclable trash! Maryam rushes back to her workshop to build a few more 3-D printers! Let’s review how we used a new equation, and a 10 by 10 grid, to find quantities and compare percents. The equation Quantity equals Percent times Whole is a useful tool when working with percents. In THIS equation, the PERCENT is written in DECIMAL form. If you know two of any of the values in this equation, you can plug them in to solve for the third. Also, we can use a 10 by 10 grid to visualize and solve for Percents, Quantities, and Wholes. Maryam ships her Recycling 3-D printers throughout the town, and they're a huge hit. People use them to build and sell every sort of product. But Maryam isn't 100 percent satisfied. Same waste, different color.