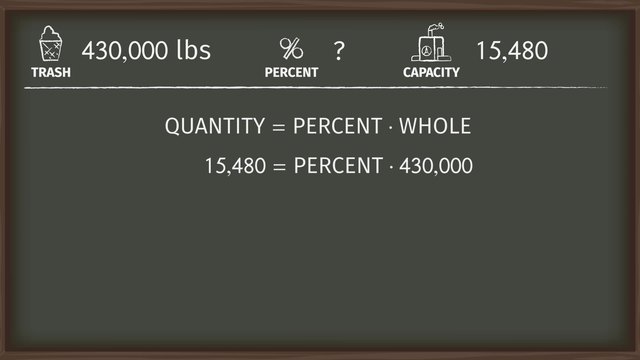
Solving Percent Problems: part and whole given
- Solving Percent Problems: Part and Whole Given
- Solving Percent Problems: Part and Whole Given – Explanation
- Solving Percent Problems: Part and Whole Given – Examples
- Solving Percent Problems: Part and Whole Given – Practice
- Solving Percent Problems: Part and Whole Given – Summary
- Solving Percent Problems: Part and Whole Given – Frequently Asked Questions


Basics on the topic Solving Percent Problems: part and whole given
Solving Percent Problems: Part and Whole Given
When dealing with percentages in mathematics, understanding how to manipulate the relationship between part, whole, and percent is essential. This skill is crucial for a variety of real-world applications, including calculating discounts, determining interest rates, and analyzing statistical data.
Solving Percent Problems: Part and Whole Given – Explanation
Percent: A measurement that represents a number as a fraction of 100.
This formula provides a straightforward method for calculating any of the three components—part, whole, or percent—given the other two. It's a basic proportion that can be rearranged to solve for the unknown quantity.
| Component | Description | Example |
|---|---|---|
| Part | The specific segment or quantity of interest within the whole. | 18 students passed the test. |
| Whole | The total or entirety of the quantity being considered. | There are 60 students in the class. |
| Percent | The part expressed as a fraction of 100. | 30% of the students passed the test. |
Solving Percent Problems: Part and Whole Given – Examples
Let’s look at an example of different situations where the missing information will be either the part, whole, or percent.
Example 1: Finding the Whole
Given: The part (number of students who passed) is 18, and the percent is 30%.
Question: How many students are in the class?
Example 2: Finding the Part
Given: The whole (total number of apples) is 50, and the percent is 20%.
Question: How many apples are red?
Example 3: Finding the Percent
Given: The part (number of red apples) is 10, and the whole (total number of apples) is 50.
Question: What percent of the apples are red?
Solving Percent Problems: Part and Whole Given – Practice
Solving Percent Problems: Part and Whole Given – Summary
Key Learnings from this Text:
Mastery of the formula $\frac{\text{Part}}{\text{Whole}} = \frac{\text{Percent}}{100}$ is vital for solving various practical problems involving percentages.
This knowledge is applicable in a range of real-life situations such as finance, academics, and everyday calculations.
Visual examples aid in the comprehension and application of these concepts in an engaging and accessible manner.
For further exploration of how these principles are applied in everyday scenarios, see Applying Percentages to the Real World.
Solving Percent Problems: Part and Whole Given – Frequently Asked Questions
Transcript Solving Percent Problems: part and whole given
Jungle Jack is a world-renowned scientist. He's written many books about his adventures, including research on the animals of Madagascar. On his current expedition, to Palm Island, he's joined by Tina, who's applying to become his long-term apprentice. If she wants to work with the famous researcher, she'll have to pass an animal-spotting test. It will require a sharp eye, as well as the ability to solve percent problems. Palm island has a population of feisty lemurs! For her first challenge, Tina has one hour to find as many lemurs as she can. Jack tells her there are a total of 20 on the island. It's almost the end of the hour, and Tina has just observed her 14th lemur. Tina wants to calculate what percent that is to see if she's passed this part. Let's organize our information in a table, showing the part observed, 14, the whole population, 20, and the percent, which we don't know yet. Since the percent is an unknown, let’s use the variable 'x' to stand for percent. Remember that a percent is a ratio, a part out of 100. We can write it as a fraction, 'x' over 100. We know Tina’s ratio of part to whole is 14 out of 20, and we want to find the percent equivalent. So we write an equation, 14 over 20 equals 'x' over 100. Notice that the fractions on both sides of the equation are part over whole. To solve, we cross-multiply. 14 times 100 equals 20 times x. Dividing both sides by 20 gives us x= 70. 14 lemurs out of 20 total is equivalent to 70 out of 100. That’s 70 percent, which is good enough to pass the first part of the test. Let's add the results to her clipboard. So where were the other 6 lemurs hiding? Oh, you tricky lemurs you. Let’s head down to the beach for Tina’s next challenge. To prove she's ready to do scientific research, Tina needs to count hermit crabs on this beach. She finds 136 crabs on the beach, and Jack tells her she's passed this portion of the test with flying colors. But Tina doesn't just want to pass the test: she wants to know everything about the island. So she asks Jungle Jack what percent she found. He tells her 85%. Can we calculate the total population of crabs from this information? Let’s add the known data to our table. We know the part observed, 136, but not the whole population. We also know the percent, 85. Let’s call our unknown whole population 'w'. 136 over 'w' equals 85 over 100. Again, let's cross-multiply. Thirteen-thousand six-hundred equals 85 "w." To isolate the variable 'w', divide by 85, giving us 'w' equals 160. Let's add that to the table. But where are the crabs that Tina couldn't find? They were at an underground rock party! And now she has her last challenge, finding the elusive hippos. They are extremely shy. Jack tells Tina there are 30 hippos in total on the island. Tina only needs to find 20% of them to pass the final test. So exactly how many hippos is that? Adding the data to the table makes this easy to set up. Let’s call the unknown part 'p'. We know the whole is 30 hippos, and she needs to find 20 percent of the total p over 30 equals 20 over 100. Cross multiplying and solving gives us "p" equals 6. While she's out searching for the hippos, let’s review what it takes to be a professional with percents. Here are the steps to solve part, whole, and percent problems. First, organize and identify your given information with the words part, whole, and percent. Then, assign a variable to the unknown information. The variable might be the part, the whole, or the percent. Now, set up a proportion relating part out of whole to your percent and solve for the variable you want to find. It's almost sunset and she's only seen 4 hippos, and she's struggling to stay awake. Luckily her new animal friends are there to help her pass the test. She will now be able to work on Palm Island for years to come. Time to celebrate with her new friends!
Solving Percent Problems: part and whole given exercise
-
Calculate the percentage of animals Tina saw today.
HintsSet up a proportion.
$\dfrac{\text{part}}{\text{whole}}=\dfrac{\%}{100}$
$\dfrac{14}{35}$ = $\dfrac{x}{100}$.
Now cross multiply.
$35x = 1400$
Solve for the missing percent by dividing both sides by $35$.
$\dfrac{35x}{35}=\dfrac{1400}{35}$
$x=40$
SolutionTo find a missing percent, set up a proportion with the percent as the variable. $\dfrac{\text{part}}{\text{whole}}=\dfrac{\%}{100}$
Here are the steps to finding one of the solutions:
$\begin{array}{l}\frac{16}{20}=\frac{x}{100}\\ \\ 16\left(100\right)=20\left(x\right)\\ \\ \frac{1600}{20}=\frac{20x}{20}\\ \\ x=80\end{array}$
-
How many of each animal did she see?
HintsThe part is missing. Use the proportion and fill in the information you already know.
$\dfrac{\text{\bf{part}}}{\text{whole}}=\dfrac{\%}{100}$
A variable can be used in place of the part.
$\dfrac{x}{60}=\dfrac{90}{100}$
Use cross multiplication to solve.
$\begin{array}{l}\frac{x}{60}=\frac{90}{100}\\ \\ 100x=5400\\ \\ \frac{100x}{100}=\frac{5400}{100}\\ \\ x=54\end{array}$
SolutionThe proportion $\dfrac{\text{\bf{part}}}{\text{whole}}=\dfrac{\%}{100}$ can be used to find the missing part observed for each animal.
For example to find the number of hippos observed, you could take the steps seen here:
$\begin{array}{l}\frac{x}{20}=\frac{50}{100}\\ \\ x\left(100\right)=50\left(20\right)\\ \\ \frac{100x}{100}=\frac{1000}{100}\\ \\ x=10\end{array}$
-
Calculate the missing percentages and numbers from the table below.
HintsTo find a missing part, whole or percent, use the formula
$\dfrac{\text{part}}{\text{whole}}=\dfrac{\%}{100}$.
Using the formula, $\dfrac{\text{part}}{\text{whole}}=\dfrac{\%}{100}$
- fill in the information you already know
- replace the missing value with a variable, such as $x$
Cross-multiplication can help you solve for the missing value.
SolutionHere you will find the solutions in the table.
-
Calculate the missing percentages and fractions.
HintsTo find a percent, the numerator is the part and the denominator is the whole.
Fractions can be converted to a percent by dividing the numerator by the denominator and then multiplying by 100.
For example, $\frac{3}{5}$ can be written as $3 \div 5$ which is equal to $0.6$. This can then be multiplied by 100, to get a percent of $60\%$.
One of the animals has 3 solutions and the other has 4 solutions.
SolutionHermit Crab: 120 out of 160
- $\frac{120}{160}$
- $\frac{60}{80}$
- $\frac{30}{40}$
- $75\%$
- $\frac{14}{20}$
- $\frac{7}{10}$
- $70\%$
-
Identify the correct order of instructions to work out the percentages.
HintsPut the information you already know into the formula: $\dfrac{\text{part}}{\text{whole}}=\dfrac{\%}{100}$
Here you will see an example of the steps taken to find a missing percentage.
Solution1) Use the formula: $\dfrac{\text{part}}{\text{whole}}=\dfrac{\%}{100}$
2) Substitute the $4$ in the part, the $16$ in the whole and a variable $x$ in the percent.
$\dfrac{4}{16}=\dfrac{x}{100}$
3) Cross multiply: $4 \times 100 = 16 \times x$
4) Divide both sides by 16 to find the solution. $400=16x$
5) The solution is found. $x=25\%$
-
Find the percentage of a number.
HintsSetting up a proportion can help find a missing percentage when the part and whole are know.
For example; 3 is what percent of 12.
The proportion used to solve would be:
$\frac{3}{12}=\frac{n}{100}$
To solve this proportion,
$\frac{3}{12}=\frac{n}{100}$
the following steps can be taken:
$\begin{array}{l}\frac{3}{12}=\frac{n}{100}\\ \\ 12\left(n\right)=3\left(100\right)\\ \\ \frac{12n}{12}=\frac{300}{12}\\ \\ n=25\end{array}$
Solution- To find a missing percent, given a part and a whole, set up a proportion: $\dfrac{\text{part}}{\text{whole}}=\dfrac{\%}{100}$
- Fill in the known information and then cross-multiply to solve for the missing value.
4 is 20% of 20
5 is 10% of 50
27 is 45% of 60