Multiplying up to Three Digits Using the Standard Algorithm
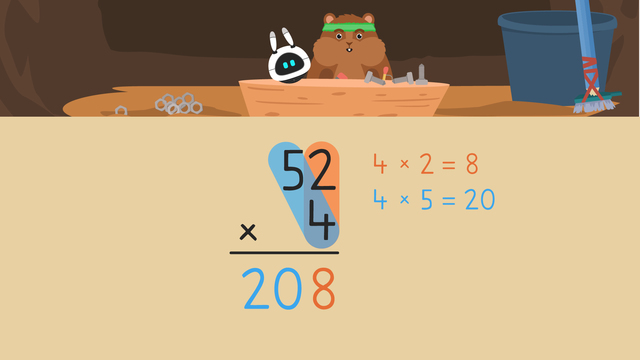

Basics on the topic Multiplying up to Three Digits Using the Standard Algorithm
Multiplication with Regrouping
What is the standard algorithm for multiplication? First, we need to know what a standard algorithm is. A standard algorithm is a step-by-step way to solve a problem. What is the standard algorithm for multiplication? Understanding the standard algorithm for multiplication just means that you know the step-by-step way to solve a multiplication problem. The standard multiplication algorithm is demonstrated and explained by multiplying multi-digit numbers.
Multiplication – Standard Algorithm
Now that we know what a standard algorithm for multiplication is, you may be wondering how to do standard algorithm multiplication. We can do multiplication by following the standard algorithm multiplication steps.
Let’s take a look at a standard algorithm multiplication example so we can see step by step standard algorithm multiplication!
In this standard algorithm multiplication example, we will be multiplying fifty-two times four. Before we can do multiplication using the standard algorithm, we must set up the problem by placing the larger factor on top, and line up the other factor below it. We must line up all the digits by place value, and include a multiplication symbol.


Now that our problem is set up for multiplication using standard algorithm, let’s solve it!
In order to calculate fifty-two times four first, multiply the bottom factor by the ones place, regrouping as needed. Four times two is eight, so we write it in the ones place.

No regrouping is needed, so we move on to the next step. Next, multiply the bottom factor by the tens place. What is the product of four times five tens? Twenty tens, and we write it in the tens and hundreds place.

When we solve fifty-two times four we get the product two hundred eight! We just did multiplication using the standard algorithm! Now that you have practiced and know what the standard algorithm in multiplication is, let’s review!
Standard Algorithm Multiplication with Regrouping – Summary
Remember: the standard algorithm of multiplication is just the steps for how to solve multiplication using the standard algorithm. Here are the steps for how to do the standard algorithm multiplication:
| Step # | What to do? |
|---|---|
| 1 | Set up the equation vertically by lining up the place values. |
| 2 | Multiply the bottom factor by the ones place, regrouping as needed. |
| 3 | Multiply the bottom factor by the tens place, regrouping as needed. |
| 4 | Repeat the pattern as needed until you have multiplied all the place values. |
Follow these simple steps if you want to practice multiplication with the standard algorithm!
Want some more standard algorithm multiplication practice? In addition to the multiplication standard algorithm video, there are more interactive exercises, worksheets and other activities on multi-digit multiplication with regrouping using the standard algorithm.
Transcript Multiplying up to Three Digits Using the Standard Algorithm
Transkripte - DACH Prozess Transkripte - DACH Prozess 100% 10 C2:J100
One afternoon long long ago, Mr. Squeaks decided to make a new invention out of spare parts. There's just one problem, all it displays is multiplication equations! Let's help Mr. Squeaks unlock his invention by... "Multiplying up to Three Digits Using the Standard Algorithm". The first equation we need to solve to help Mr. Squeaks is fifty-two times four. When we multiply numbers using the standard algorithm... ...we place the larger factor on top, and line up the other factor below it. We MUST line up all the digits by place value, and include a multiplication symbol. In order to calculate fifty-two times four... first, multiply the bottom factor by the ones place, regrouping as needed. Four times two is eight... so we write it in the ones place HERE. No regrouping is needed, so we move on to the next step. Next, multiply the bottom factor by the tens place. What is the product of four times five tens? (...) Twenty tens, and we write it HERE. The product of fifty-two times four is two hundred eight. Mr. Squeaks enters the product on the robot and... another equation appears! Now, we'll calculate eighty-six times nine. First, set up the equation vertically by lining up the place values. (...) Then, multiply the bottom factor by the ones place, regrouping as needed. What is the product of nine times six? (...) Fifty-four, but fifty-four does not fit in the ONES place... so we put four in the ones place (...) and regroup five TENS here. Next, multiply the bottom factor by the tens place. What is the product of nine times eight tens? (...) Seventy-two tens, but we're not finished yet. Since we regrouped five tens to the tens place, we MUST add them. Seventy-two tens PLUS five tens is seventy-seven tens. The product of eighty-six times nine is seven hundred seventy-four. Mr. Squeaks enters the product on the robot, and... one final equation appears! Last, we'll calculate two hundred ninety-three times seven. First, set up the equation vertically by lining up the place values. (...) Next, multiply the bottom factor by the ones place, regrouping if needed. What is the product of seven times three? (...) Twenty-one, so we put one in the ONES place... and regroup two tens HERE. Then, multiply the bottom factor by the tens place. What is the product of seven times nine tens? (...) Sixty-three tens. Now, add the two tens we regrouped. Sixty-three plus two is sixty-five... so we put five in the tens place (...) regrouping six to the hundreds place. We have three digits this time, so we continue solving. Next, multiply seven times two hundreds... to get fourteen hundreds. Are we finished? (...) Not until we add the six hundreds we regrouped. Forteen hundreds plus six hundreds is twenty hundreds (...) and we write it HERE. Don't forget your comma! The product of two hundred ninety-three times seven (...) is two thousand fifty-one! Remember (...) when we multiply numbers up to three digits using the standard algorithm... the first step is to set up the equation vertically by lining up the place values. The second step is to multiply the bottom factor by the ones place, regrouping as needed. The third step is to multiply the bottom factor by the tens place, regrouping as needed. The fourth step is to repeat the pattern as needed until you have multiplied all the place values. Okay Mr. Squeaks, is your invention working? Mr. Squeaks has a new robot friend (...) and it looks like he's called them Imani! What would you name his new friend? Write your name ideas in the comments below! To enable screen reader support, press ⌘+Option+Z To learn about keyboard shortcuts, press ⌘slash
One afternoon long long ago, Mr. Squeaks decided to make a new invention out of spare parts. There's just one problem, all it displays is multiplication equations! Let's help Mr. Squeaks unlock his invention by... "Multiplying up to Three Digits Using the Standard Algorithm". The first equation we need to solve to help Mr. Squeaks is fifty-two times four. When we multiply numbers using the standard algorithm... ...we place the larger factor on top, and line up the other factor below it. We MUST line up all the digits by place value, and include a multiplication symbol. In order to calculate fifty-two times four... first, multiply the bottom factor by the ones place, regrouping as needed. Four times two is eight... so we write it in the ones place HERE. No regrouping is needed, so we move on to the next step. Next, multiply the bottom factor by the tens place. What is the product of four times five tens? (...) Twenty tens, and we write it HERE. The product of fifty-two times four is two hundred eight. Mr. Squeaks enters the product on the robot and... another equation appears! Now, we'll calculate eighty-six times nine. First, set up the equation vertically by lining up the place values. (...) Then, multiply the bottom factor by the ones place, regrouping as needed. What is the product of nine times six? (...) Fifty-four, but fifty-four does not fit in the ONES place... so we put four in the ones place (...) and regroup five TENS here. Next, multiply the bottom factor by the tens place. What is the product of nine times eight tens? (...) Seventy-two tens, but we're not finished yet. Since we regrouped five tens to the tens place, we MUST add them. Seventy-two tens PLUS five tens is seventy-seven tens. The product of eighty-six times nine is seven hundred seventy-four. Mr. Squeaks enters the product on the robot, and... one final equation appears! Last, we'll calculate two hundred ninety-three times seven. First, set up the equation vertically by lining up the place values. (...) Next, multiply the bottom factor by the ones place, regrouping if needed. What is the product of seven times three? (...) Twenty-one, so we put one in the ONES place... and regroup two tens HERE. Then, multiply the bottom factor by the tens place. What is the product of seven times nine tens? (...) Sixty-three tens. Now, add the two tens we regrouped. Sixty-three plus two is sixty-five... so we put five in the tens place (...) regrouping six to the hundreds place. We have three digits this time, so we continue solving. Next, multiply seven times two hundreds... to get fourteen hundreds. Are we finished? (...) Not until we add the six hundreds we regrouped. Forteen hundreds plus six hundreds is twenty hundreds (...) and we write it HERE. Don't forget your comma! The product of two hundred ninety-three times seven (...) is two thousand fifty-one! Remember (...) when we multiply numbers up to three digits using the standard algorithm... the first step is to set up the equation vertically by lining up the place values. The second step is to multiply the bottom factor by the ones place, regrouping as needed. The third step is to multiply the bottom factor by the tens place, regrouping as needed. The fourth step is to repeat the pattern as needed until you have multiplied all the place values. Okay Mr. Squeaks, is your invention working? Mr. Squeaks has a new robot friend (...) and it looks like he's called them Imani! What would you name his new friend? Write your name ideas in the comments below! Turn on screen reader support
Multiplying up to Three Digits Using the Standard Algorithm exercise
-
Arrange the steps for solving a multiplication problem.
HintsThe first step is to set up the equation vertically by lining up the place values.
Multiply each place value starting with the ones place, regrouping when you need to.
Repeat the pattern until you have multiplied all the place values.
SolutionIn order to calculate 971 x 2:
- First, set up the equation vertically by lining up the place values of 971 and 2
- Second, multiply 2 x 1 = 2
- Then, multiply 2 x 7 = 14, regrouping the 1 to the hundreds place
- Now, multiply 2 x 9 = 18, and add 18 + 1 = 19
- Write the 19 below, which gives us the answer 1,942
-
Which factors do we multiply first?
HintsFirst, multiply the ones place.
Next, multiply the tens place.
Solution- We highlight the 8 x 6 in yellow, since we multiply the ones place first
- We highlight the 8 x 4 in blue, since we multiply the tens place second
-
What is 38 x 5?
HintsFirst, multiply the bottom factor by the factor in the ones place.
In this illustration, you can see the steps for solving, starting with the orange highlight.
SolutionIn order to calculate 38 x 5:
- First, multiply the 5 x 8 = 40. Write 0 in the ones place, and regroup the 4 to the tens place
- Next, multiply 5 x 3 = 15
- Then, add 15 + 4 = 19
- Last, record 19, which gives us the answer 190
-
What is 861 x 7?
HintsFirst, multiply 7 x 1.
Then, multiply 7 x 6. Last, multiply 7 x 8. Don't forget to regroup if you need to!
Solution- First multiply 7 x 1 = 7
- Next, multiply 7 x 6 = 42. Write the 2 in the tens place and regroup the 4 to the hundreds place
- Then, multiply 7 x 8 = 56. Add 56 + 4 = 60, which gives us the product 6,027
-
What is 13 x 3?
HintsMultiply each place value, starting with the ones place.
Multiply 3 x 3, then multiply 3 x 1.
Solution- First, 3 x 3 = 9. Place a 9 in the equation on the right and in the product below
- Next, multiply 3 x 1 = 3. Place a 3 in the equation on the right, and in the product below to get the final answer 39
-
Complete each step for solving a multiplication equation using the standard algorithm.
HintsAlways start by multiplying the smallest place value on the right side of the equation, and work your way to the left.
Begin by multiplying the ones.
Solution- First, multiply the bottom number, 3 by the ones place, 8. 3 x 8 = 24. Write the 4 in the product, and regroup the 2 to the tens place.
- Next, multiply the bottom number, 3 by the tens place, 3. 3 x 3 = 9. Add 9 and the 2 we regrouped, which equals 11. Write the 1 in the product, and regroup the 1 to the hundreds place.
- Last, multiply the bottom number, 3 by the hundreds place, 4. 3 x 4 = 12. Add 12 and the 1 we regrouped, which equals 13. Write 13 in the space below to get the final product 1,314.
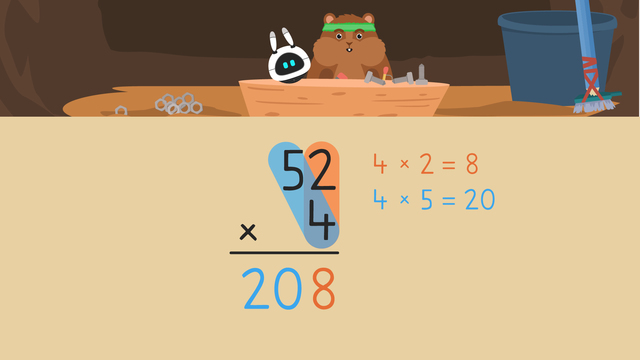
Multiplying up to Three Digits Using the Standard Algorithm
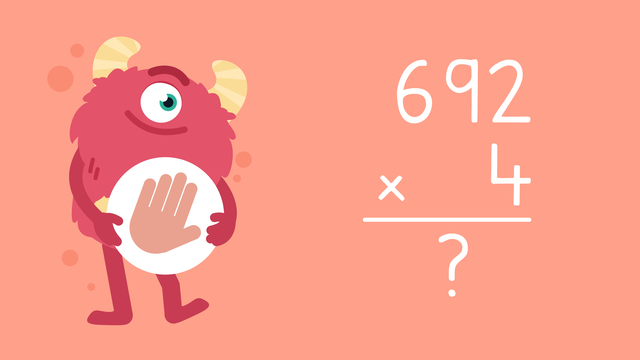
Multiplying up to Three Digits Using the Standard Algorithm—Let's Practice!

Multiplying Two-Digit Numbers by Two-Digit Numbers
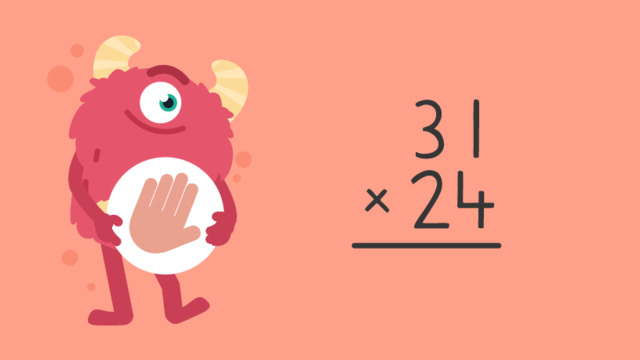
Multiplying Two-digit Numbers by Two-digit Numbers — Let's Practice!
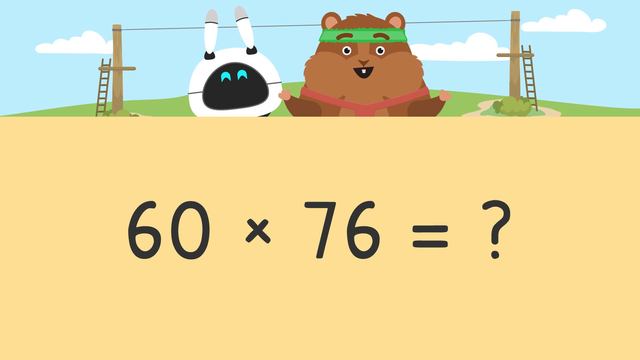
Multiplying 2-Digit Numbers by Multiplies of 10

Multiplying Tens, Hundreds and Thousands
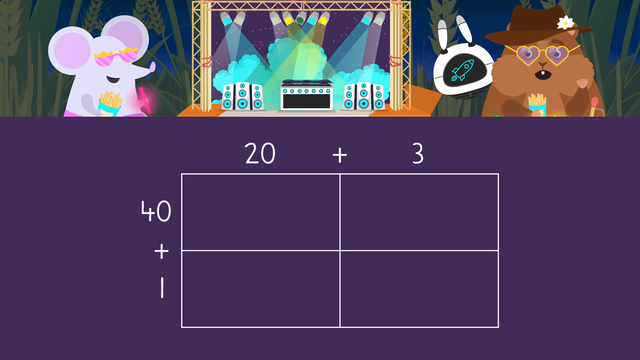
Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model
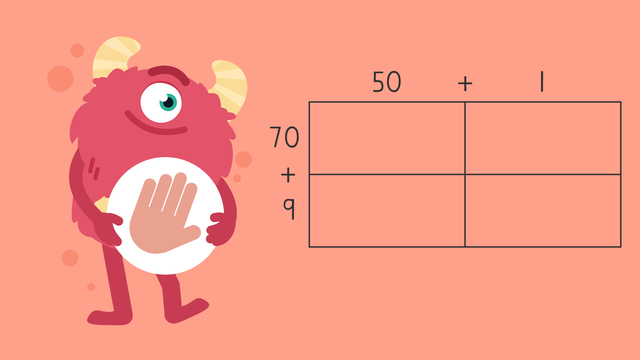
Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model—Let's Practice










the name should be Cortexa
I think his name should be Bot’e
Roller coaster with you