Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model

Basics on the topic Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model
Area Models in Multiplication
What is an Area Model for Multiplication? An area model is a rectangular model that can be used as a tool when multiplying 2-digit numbers by 2-digit numbers. Area model multiplication can also be used for multiplication for all types of digits, however it is mostly used to multiply larger numbers since it breaks them down and makes them easier to work with.
In the next section, you will see an example of area model multiplication 2 digit by 2 digit using a multiplication area model.
Multiplying 2 Digit by 2 Digit Numbers using Area Models
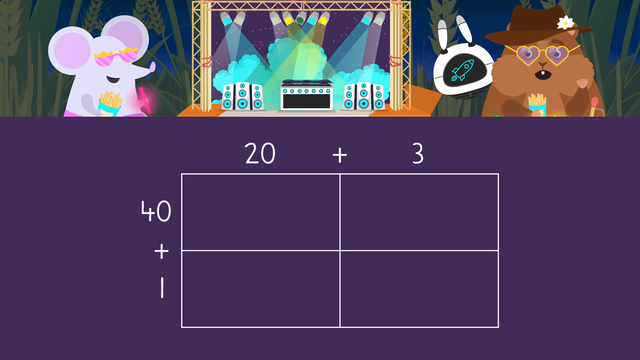
Let's use an area model to help us multiply twenty-three times forty-one.
In the video, Mr. Squeaks and Imani are preparing for the Fry Festival, featuring a special guest surprise DJ! Before the show starts they need to calculate how many glow sticks and fries they have for the audience by multiplying 2-digit by 2-digit numbers. In order to help them, let’s learn how to do area model multiplication.
The first step is to set up the area model. Start by drawing a rectangle. Next, split it into parts based on how many place values are in each number. Twenty-three has two place values tens and ones, so split the rectangle in two parts vertically. Forty-one also has two place values tens and ones, so split the rectangle in two parts horizontally.
Next, label each part by writing the factors in expanded form. The value of the two in the tens place is twenty and the value of the three in the ones place is three, so label the top twenty plus three. Next the value of the four in the tens place is forty and the value of the one in the ones place is one, so label the left side with forty plus one.
The second step is to multiply each corresponding pair to find the partial products. Partial products are the answers we get when each factor pair is multiplied.
The third step is to add all the partial products.
[line 36: twenty-three-times-forty-one-area-model-four-parts-twenty-times-forty-equals-eight-hundred-twenty-times-one-equals-one-three-times-forty-equals-one-hundred-twenty-three-times-one-equals-three-eight-hundred-plus-one-hundred-twenty-plus-twenty-plus-three-multiplication-2-digit-by-2-digit]
The product of twenty-three and forty one is nine hundred forty-three.
Area Models for Multiplication – Summary
When multiplying multiplying 2-digit numbers by 2-digit numbers using an area model follow these simple steps:
| Step # | What to do |
|---|---|
| 1 | Set up the area model by drawing a rectangle and separating it into parts based on how many place values are in each number and label each side with each factor written in expanded form. |
| 2 | Multiply each corresponding pair to find the partial products. |
| 3 | Find the sum of all the partial products. |
Have you practiced yet? On this website you can practice area model multiplication 2 digit by 2 digit and find an area model multiplication worksheet and area model multiplication worksheets, along with other activities, and interactive exercises.
Transcript Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model
Mr. Squeaks and Imani are preparing for the Fry Festival. "Ohhhhhh Imani I can't wait! I wonder who the guest DJ is!?!?" "I wonder if it's DJ Aberhamster Lincoln!" Before the show starts, Mr. Squeaks and Imani need to calculate how many glow sticks and fries they have for the audience. Let's help them solve by... Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model. An area model is a rectangular model that helps us find the product of two numbers. First, we need to calculate how many glow sticks they have. There are twenty-three boxes with forty-one in each. We will use an area model to help us multiply twenty-three times forty-one. The first step is to set up the area model. Start by drawing a rectangle. Next, split it into parts based on how many place values are in each number. Twenty-three has two place values (...) TENS and ONES, so split the rectangle in two parts vertically. Forty-one also has two place values (...) TENS and ONES, so split the rectangle in two parts horizontally. Next, label each part by writing the factors in expanded form. The value of the two in the tens place is twenty and the value of the three in the ones place is three... so label the TOP twenty plus three. Next the value of the four in the tens place is forty and the value of the one in the ones place is one... so label the LEFT SIDE with forty plus one. The second step is to multiply each corresponding pair to find the partial products. Partial products are the answers we get when each factor pair is multiplied. In THIS box, (...) multiply twenty and forty... to get eight hundred. In THIS box, (...) multiply twenty and one... to get twenty. Next, multiply three and forty... to get one hundred twenty. Last, multiply three and one... to get three. The third step is to ADD all the partial products. Eight hundred plus (...) one hundred twenty plus (...) twenty plus (...) three is (...) nine hundred forty-three. They have nine hundred forty-three glow sticks! Now, we need to calculate how many fries they have. There are sixty-eight boxes with ninety-five in each, so we multiply sixty-eight times ninety-five. The first step is to set up our area model by drawing a rectangle. Since each number has two place values we separate it into four parts. Next, label each part by writing the factors in expanded form. How do we label each part? (...) Label the TOP sixty plus eight... and label the LEFT SIDE ninety plus five. What is the second step? (...) The second step is to multiply each corresponding pair to find the partial products. In THIS box, (...) multiply sixty and ninety... to get five thousand four hundred. In THIS box, (...) multiply sixty and five... to get three hundred. Next, multiply eight and ninety... to get seven hundred twenty. Last, multiply eight and five... to get forty. What is the final step? (...) The final step is to ADD all the partial products. Five thousand four hundred plus (...) seven hundred twenty plus (...) three hundred plus (...) forty (...) equals six thousand four hundred sixty. That means there are six thousand four hundred sixty fries for the festival (...) WOW! Remember (...) when multiplying two digit numbers by two digit numbers using an area model... the first step is to set up the area model by drawing a rectangle and separating it into parts based on how many place values are in each number... and label each side with each factor written in expanded form. The second step is to multiply each corresponding pair to find the partial products. The third step is to find the sum of all the partial products. Since DJ Aberhamster couldn't make it today, (...) everyone give it up for our special guest (...) DJ Imani!
Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model exercise
-
An area model is used as a strategy to solve what kind of equations?
HintsThink about finding the area of a rectangle. What operation would you use?
An area model is a strategy used when you are looking to get a larger number
SolutionWe use an area model to solve a multiplication equation. An area model helps us break down two digit numbers by place value to help us find the product. We can use an area model as a strategy for finding the product of larger numbers.
-
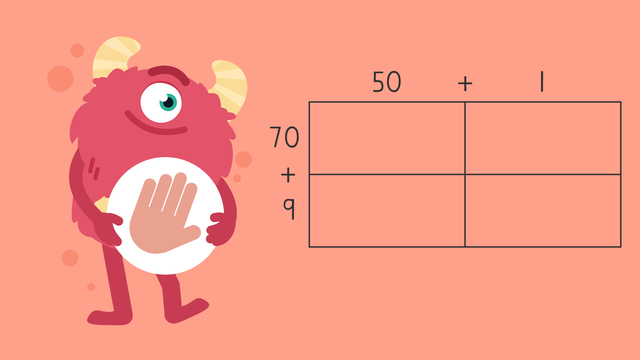
In the equation 45 x 72, what is the expanded form of 72?
HintsRemember, we look at a number from left to right. For example, the number 67; the 6 is the first digit and it is in the tens place. The 7 is the last digit, and it is in the ones place.
Draw an area model of you own, what do you notice?
How would you create the number 72?
Think about the number 62. The 6 is in the tens place which means the value of the 6 is 60 because it is 6 groups of ten.
SolutionThe correct answer is 70 + 2. Expanded form means you are writing each factor based on place value. The 7 is in the tens place which means its value is 70 because there are seven groups of ten. The 2 is in the ones place which means its value is 2.
-
What are the steps to creating an area model that help us solve 2 digit by 2 digit multiplication?
HintsAn area model for multiplying is a rectangle with the expanded form of a number on the top and side.
Expanded form is when you expand the factors based on the value of the tens and ones place for each number.
How many place values are in each number?
Look at the area model, how is it set up?
SolutionThe steps for solving a multiplication equation using an area model are as follows:
- First, set up an area model by drawing a rectangle and separating it into parts based on how many place values are in each number. Next, label each side with each factor in expanded form.
- The second step is to multiply each corresponding pair to find the partial products.
- Finally, find the sum of all the partial products.
-
Solve the equation 34 x 52
HintsDraw an area model
Find partial products and then add them together
SolutionThe correct answer is 1,768. Set up your area model by expanding 34 across the top of you box into 30 + 4 and expand 52 into 50 + 2. Next step is to multiply the corresponding boxes to find the partial products: 30 x 50= 1,500 30 x 2= 60 4 x 50 = 200 4 x 2= 8 Last step is to add the partial products together to get your final product 1,500 + 60 + 200 + 8= 1,768
-
Create an area model using the digits that have been provided.
HintsRemember, place means where the digit is located within a number and value means how much the digit is worth.
Use place value to expand your numbers.
Here is an example of an area model for 58 x 22.
SolutionThe solution is to expand your factors based on the value. In the factor, 94, the value of the 9 in the tens place is 90. The value of the 4 in the ones place is 4. So, you label horizontally across the top, 90 + 4. In the factor, 63, the value of the 6 in the tens place is 60. The value of the 3 in the ones place is 3. So, you label vertically down the side, 60 + 3.
You can also expand 63 across the top as 60 + 3 and expand 94 along the side as 90 + 4. It does not matter which number you expand across the top versus along the side as long as you expand them correctly.
-
Complete the area model.
HintsRemember, once you have expanded the number, you multiply the corresponding pairs to find the partial products.
Multiply each corresponding box one at a time to avoid making a mistake.
To find the final product, what operation do you use?
SolutionSince you were already given the expanded form, you skip that step and go right to the next step which is to multiply each corresponding pair to find a partial product.
For the area model on the left, we find the following partial products:
- 80 x 40 = 3,200
- 2 x 40 = 80
- 80 x 6 = 540
- 2 x 6 = 12
- 20 x 10 = 200
- 9x10 = 90
- 20 x 6 = 120
- 9 x 6 = 54
So 82 x 46 would be, 3,200 + 80 + 80 x 6 + 12 = 3,932
29 x 16 would be, 200 + 90 + 120 + 54 = 464
Multiplying up to Three Digits Using the Standard Algorithm
Multiplying up to Three Digits Using the Standard Algorithm—Let's Practice!

Multiplying Two-Digit Numbers by Two-Digit Numbers
Multiplying Two-digit Numbers by Two-digit Numbers — Let's Practice!
Multiplying 2-Digit Numbers by Multiplies of 10

Multiplying Tens, Hundreds and Thousands

Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model
Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model—Let's Practice












