Multiplying Two-Digit Numbers by Two-Digit Numbers


Basics on the topic Multiplying Two-Digit Numbers by Two-Digit Numbers
2-Digit by 2-Digit Multiplication
Multiplication is a mathematical operation you are probably already used to. But how do you multiply 2-digit numbers by 2-digit numbers without regrouping? Here you can learn how to multiply by double digits. After learning how to multiply 2-digit numbers, check out our double digit multiplication worksheets and practice exercises!
Multiplying by two digit numbers can be done in a few easy steps:
| Step # | What to do |
|---|---|
| 1 | Multiply the ones placed in the bottom factor by both place values in the top factor, regrouping as needed. |
| 2 | Add a placeholder, or zero. |
| 3 | Multiply the tens place in the bottom factor by both place values in the top factor, regrouping as needed. |
| 4 | Add the partial products to get the total. |
If you are still wondering how to do double digit multiplication, look at the example below.
Multiplying Two Digit by Two Digit Numbers – Example
In this example, we will be multiplying by 2-digit numbers in order to find out how many sunflower seeds they have. Since there are forty-eight containers with thirty-two in each, we will find the product of forty-eight and thirty-two.
The first step is to multiply the ones place in both factors, so we multiply two times eight to get sixteen, regrouping the one to the tens place. Next multiply two times four to get eight, adding the one we regrouped to get nine.
The second step is to add the placeholder, or zero.
The third step is to multiply the tens place in the bottom factor by both place values in the top factor. We multiply three and eight to get twenty-four, and regroup the two to the tens place. Next multiply three times four to get twelve, adding the two we regrouped to get fourteen.
The last step is to add the partial products ninety-six and one thousand four hundred forty to get the final product. Forty-eight times thirty-two is one thousand five hundred thirty-six.
Multiplying Two-Digit Numbers by Two-Digit Numbers – Summary
Remember, if someone asks you “how did you multiply 2-digit numbers by 2-digit numbers?” you can tell them to follow these easy steps:
- Multiply the ones placed in the bottom factor by both place values in the top factor, regrouping as needed.
- Add a placeholder, or zero.
- Multiply the tens place in the bottom factor by both place values in the top factor, regrouping as needed.
- Add the partial products.
Multiplying doubles takes a lot of practice. Have you practiced yet? On this website you can find a multiplying by two digit numbers worksheet, activities, and exercises.
Transcript Multiplying Two-Digit Numbers by Two-Digit Numbers
When a cool breeze whizzed through Mr. Squeaks' and Imani's home, they started to harvest some food into containers for winter. They've collected corn and sunflower seeds for their hibernation... but they need help calculating how much they have. In order to do that, we need to practice [title] "Multiplying Two-Digit Numbers by Two-Digit Numbers". They have thirteen containers with twenty-one cobs of corn in each. We need to find the product of thirteen times twenty-one. The first step is to multiply the ONES place in the bottom factor by BOTH place values in the top factor. Start by multiplying the factors in the ONES place. Which numbers are in the ONES place? (...) The bottom factor has a ONE, and the top factor has a THREE... so multiply one times three to get the product (...) three. We make sure to put the three in the ONES place, because that is the place value we multiplied. Next multiply the ONES place in the bottom factor by the TENS place in the top factor. One times one equals (...) one. We make sure to put the one in the TENS place, because that is the place value we multiplied. Now that we've multiplied the ones place by both numbers in the top factor... the second step is to add a placeholder, or a zero HERE. [zero will be added in animation to the desired spot] A placeholder is used because we are multiplying the TENS place in the bottom number next, so we write the products starting in the TENS place. Now multiply the TENS place in the bottom number by the ONES place in the top number. Two times three equals (...) six. Next multiply the two and one in the TENS place to get the product (...) two. Last, find the sum of the partial products thirteen and two hundred sixty. (...) Thirteen times twenty-one is two hundred seventy-three. [impressed]That's a lot of corn! Next, let's calculate how many sunflower seeds they have. There are forty-eight containers with thirty-two in each. The first step is to multiply the ONES place in the bottom factor by BOTH place values in the top factor. What do we get when we multiply the ONES place in both factors? (...) Two times eight is sixteen, (...) and since sixteen is a TWO DIGIT number we need to regroup... so write the six HERE and regroup the one to the tens place HERE. Next, multiply the ONES place in the bottom factor by the TENS place in the top factor. Two times four is (...) eight, and add the one we regrouped to get (...) nine. Before we move on, cross out the ONE that we regrouped (...) that way, if we need to regroup later we won't get confused. The second step is to add the placeholder HERE. Next, multiply BOTH place values in the top factor by the TENS place in the bottom factor. Three times eight is (...) twenty four... so write the four HERE and regroup the two to the tens place HERE. Next, multiply three times four (...) to get twelve... and add the two we regrouped to get (...) fourteen. The last step is to find the sum of the partial products ninety-six and one thousand four hundred forty. Mr. Squeaks and Imani have one thousand five hundred thirty-six sunflower seeds. Remember (...) when you multiply a two-digit number by a two-digit number you first... "Multiply the ONES place in the bottom factor by both place values in the top factor", regrouping as needed. The second step is to, "add a placeholder". The third step is to, "Multiply the TENS place in the bottom factor by both place values in the top factor", regrouping as needed. The last step is to find the sum of the partial products to get the final answer. After all that calculating, Mr. Squeaks realizes he has even more food than he thought... ...because Imani doesn't have a mouth to eat all that food! ...So, what does Imani eat? [animation shows him feeding her 'robot food']
Multiplying Two-Digit Numbers by Two-Digit Numbers exercise
-
Can you remember how to multiply a 2-digit number by another 2-digit number?
HintsDo you multiply the top number by the tens or the ones in the bottom number first?
The picture gives you a clue about where to start when multiplying a 2-digit number by another 2-digit number.
The partial products are the values you have once you halve multiplied both digits in the bottom number by both digits in the top number.
How do you find your final answer?
SolutionWhen multiplying a 2-digit number by another 2-digit number you:
- Multiply the ones in the bottom number by both of the digits in the top number.
- Add the zero (placeholder).
- Multiply the tens in the bottom number by both digits in the top number.
- Add the partial products to calculate the answer.
-
Can you complete the multiplication equation?
HintsDon't forget to put the 0 as a placeholder.
Remember to add on any tens you have carried over.
SolutionHere is the completed equation.
Mr Squeaks has 516 pieces of corn in his new batch.
____________________________________________________
- The first part of the equation had been done for you. 2 x 3 = 6 which was written in the ones place and 1 x 3 = 3 which was written in the tens place. We can see these numbers in red.
- Next we need to add the zero as a placeholder in the ones column.
- We then multiply 2 x 4 to get 8 and write that in the tens column.
- Next we multiply 1 x 4 to get 4 and write that in the hundreds column. We can see these numbers in blue.
- Finally we add up the digits in each place value column to find our answer.
- 6 + 0 = 6 so we write this in the ones column.
- 3 + 8 = 11 so we write 1 in the tens column and carry 1 over.
- We therefore add 4 + 1 which equals 5 and write that in the hundreds column.
- Our answer is 516.
-
Solve the multiplication problem.
HintsRead the information carefully to figure out which numbers you are multiplying.
Use a pencil and paper to write out the equation.
Don't forget the zero!
Remember to add on any numbers you have carried over.
SolutionHere is 36 x 49 written out using this method.
- First we multiplied the 9 in 49 with both digits in 36. 6 x 9 is 54 so we write the 4 below the ones and carry the 5 across. We then multiply 3 x 9 which is 27 and add the 5 we carried which equals 32. We write the 2 below the tens and the 3 in the hundreds column. We can see these numbers in red.
- Next, we put the 0 as the placeholder in the ones column.
- We then multiply the 4 in 49 with both digits in 36. 6 x 4 is 24 so we write 4 in the tens column and carry the 2 across. 3 x 4 is 12 plus the 2 we carried is 14 so we write 4 in the hundreds column and 1 in the thousands column. We can see these numbers in blue.
- Finally we add the partial products to get 1764.
- 36 x 49 = 1764
-
Can you match the multiplication problems with the correct answers?
HintsYou could use a pen and paper to write each equation out.
Have a look at this example. Does it give you a clue as to where to start?
Don't forget about the placeholder!
Remember, when you multiply the ones place of the bottom number with the ones place of the top number this gives you a clue as to what number will be in the ones place of the final answer.
After you have multiplied with the ones place of the bottom number, what do you multiply next?
SolutionHere is 14 x 23 written out using this method.
- First we multiplied the 3 in 23 with both digits in 14. 4 x 3 is 12 so we write the 2 below the ones and carry the 1 across. We then multiply 1 x 3 which is 3 and add the 1 we carried which equals 4. We write this below the tens. We can see these numbers in red.
- Next, we add the 0 as the placeholder in the ones column.
- We then multiply the 2 in 23 with both digits in 14. 4 x 2 is 8 so we write this in the tens column. 1 x 2 is 2 so we write this in the hundreds column. We can see these numbers in blue.
- Finally we add the partial products to get 322.
- 14 x 23 = 322
___________________________________________________
Following the same steps we can also work out that:
- 24 x 21 = 504
- 33 x 25 = 825
- 44 x 27 = 1188
-
Which jar should Mr Squeaks put the seeds in?
HintsUse the multiplication equation in the header to help you.
What do we need to do once we have the two partial products?
Add the ones, then the tens, then the hundreds. Don't forget any numbers you have carried over.
SolutionHere is what the completed equation looks like.
Mr Squeaks has a new batch of 294 seeds so needs to put it in the jar with the label 294!
____________________________________________________
- We already had the partial products multiplied for us so we needed to add them together to find the total.
- 4 + 0 = 4 so we write 4 in the ones place.
- 1 + 8 = 9 so we write 9 in the tens place.
- We then just have 2 in the hundreds place with nothing to add to it so we write 2 in the hundreds place at the bottom.
- We therefore have a total of 294.
-
Complete the multiplication equations.
HintsUse a pencil and some paper to write out each equation.
Think about which part of each number is multiplied first and which part is multiplied second.
Don't forget to put the zero as the placeholder!
SolutionHere is 63 x 42 written out using this method.
- First we multiplied the 2 in 42 with both digits in 63. 3 x 2 is 6 so we write the 6 below the ones. We then multiply 6 x 2 which is 12. We write 2 below the tens and 1 in the hundreds column.
- Next, we put the 0 as the placeholder in the ones column.
- We then multiply the 4 in 42 with both digits in 63. 3 x 4 is 12 so we write the 2 in the tens column and carry the 1. 6 x 4 is 24 plus the 1 we carried is 25 so we write 5 in the hundreds column and 2 in the thousands column.
- Finally we add the partial products to get 2646.
- 63 x 42 = 2646
___________________________________________________
Following the same steps we can also work out that:
- 57 x 39 = 2223
- 81 x 23 = 1863
- 92 x 37 = 3404
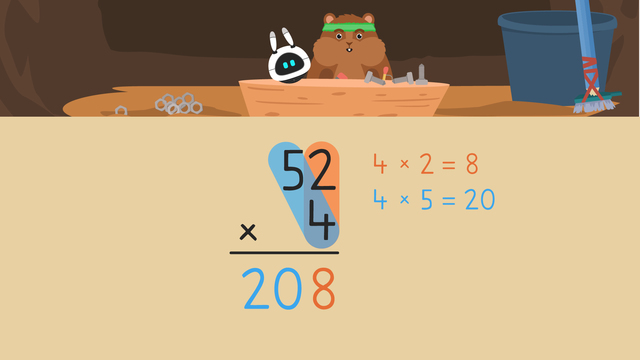
Multiplying up to Three Digits Using the Standard Algorithm
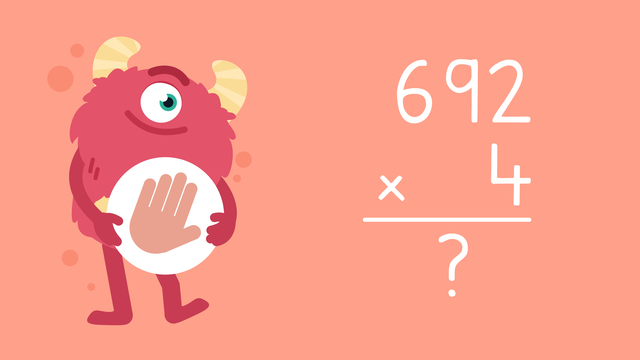
Multiplying up to Three Digits Using the Standard Algorithm—Let's Practice!

Multiplying Two-Digit Numbers by Two-Digit Numbers
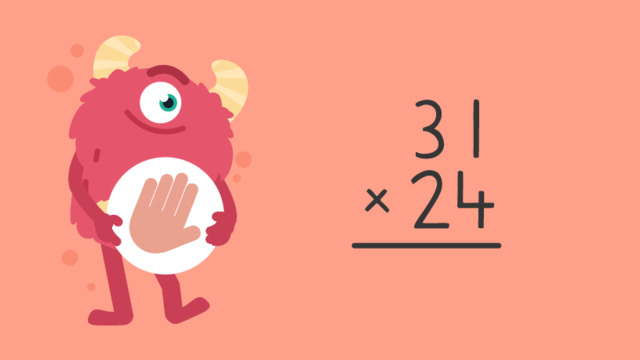
Multiplying Two-digit Numbers by Two-digit Numbers — Let's Practice!
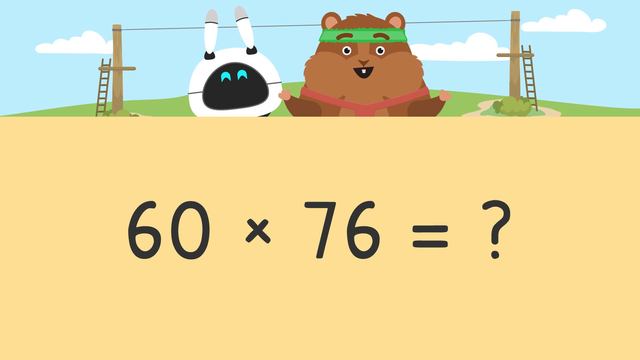
Multiplying 2-Digit Numbers by Multiplies of 10

Multiplying Tens, Hundreds and Thousands
Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model
Multiplying Two-Digit Numbers by Two-Digit Numbers Using an Area Model—Let's Practice













