Adding Tenths and Hundredths
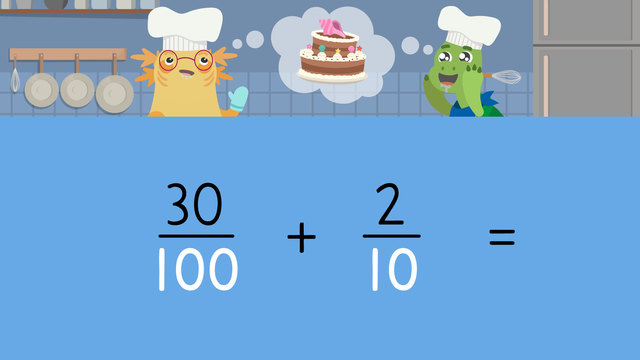

Basics on the topic Adding Tenths and Hundredths
Adding Fractions – Tenths and Hundredths
Sometimes, a problem may ask you to add two fractions that don’t share the same denominator such as adding tenths and hundredths. But how do you add tenths and hundredths? Find out all you need to know about adding fractions with uneven denominators with the example in this text and by watching the video.
Adding Tenths and Hundredths– Example
How do you add fractions with uneven denominators? When adding fractions with tenths and hundredths, first, set up the problem.
Next, look at the denominator, the bottom number, of both fractions. Since they’re not the same, or like, we need to convert one fraction to have the same denominator as the other.
To do this, we can multiply to fractions with the ten denominator by ten to make one hundred. When we do this, we also need to multiply the numerator, the top number, by ten as well.
Now both denominators are one hundred, we can solve the problem!
Adding Tenths and Hundredths – Summary
Remember, when adding tenths and hundredths fractions, make sure you have like denominators before solving the problem. The denominator of the sum will always remain the same, and you only need to add together the numerators. The illustration below shows what you need to keep in mind when adding tenths and hundredths.
Below, you can see the necessary steps to adding fractions with uneven denominators.
| Step # | What to do |
|---|---|
| 1 | Set up the problem and look at the denominators. |
| 2 | Multiply the smaller denominator until it matches the other denominator. Remember to multiply the numerator as well. |
| 3 | Once both denominators are the same, add the numerators. The sum is your result. |
After watching this video, you will find more interactive exercises, worksheets and further activities on adding tenths and hundredths with questions and answers.
Transcript Adding Tenths and Hundredths
Axel has decided to bake a delicious cake with leftover ingredients. "Hey Tank, I need you to calculate how much flour is left, and while you're at it, do the same for the sugar, please!" Let's help Tank calculate the total flour and sugar Axel has to bake with by adding tenths and hundredths. A tenth represents one part of a whole divided into ten equal parts. We can represent tenths as a fraction by writing the parts we have for the numerator, over a denominator of ten. A hundredth represents one part of a whole divided into one hundred equal parts. We can represent hundredths as a fraction by writing the parts we have for the numerator, over a denominator of one hundred. Let's practice adding the leftover bags of flour together. One bag has seventy-seven hundredths of flour, and the other bag has one-tenth. We are solving seventy-seven hundredths plus one-tenth. First, make sure both fractions have the same, or like, denominators. Tenths and hundredths are not like denominators, so we need to multiply the tenths fraction by ten, because it is the least common multiple of ten and one hundred! Ten times ten is one hundred. Since we multiplied the denominator of the tenths fraction by ten, we must do the same for its numerator. One times ten is ten. One tenth and ten hundredths are equivalent fractions. Now, we can add the fractions because both denominators are one hundred! The denominator remains one hundred since we are adding. Then, add the numerators. Seventy-seven plus ten equals eighty-seven. Axel has eighty-seven hundredths of flour to bake with. Now we know how to add tenths and hundredths, let's help Tank solve how much sugar Axel has to bake with! One bag of sugar has thirty-hundredths left, and the other bag has two-tenths left. We are solving thirty hundredths plus two-tenths. What is the first step? Make sure the fractions have like denominators. How can we make like denominators with these fractions? Multiply the numerator and denominator of the tenths fraction by ten. Ten times ten is one hundred. Two times ten is twenty. Two tenths and twenty hundredths are equivalent fractions. What is the final step? Add the fractions. The denominator remains one hundred. Thirty plus twenty equals fifty. We can simplify fifty-hundredths because fifty goes into both fifty and one hundred. Fifty goes into one hundred two times. Fifty goes into fifty one time. Axel has one half a bag of sugar for baking his cake! While Axel bakes the cake, let's review! Remember, when adding tenths and hundredths, first, make sure both fractions have the same, or common, denominators. Second, keep the denominator the same in the sum, since this never changes when adding fractions. Third, add together the numerators. Don't forget to simplify when possible! "It's ready, Tank!" "Oh boy, I have been dreaming of this cake all day!"
Adding Tenths and Hundredths exercise
-
Identify the different parts of the equation.
HintsThe numerator is above the fraction bar, and indicates how many pieces of the whole are being used in this fraction.
The 6 in this fraction is the denominator.
The operation used in this equation is addition.
SolutionThe numerator is always above the fraction bar, and indicates how many pieces of the whole we are using in this fraction.
The denominator is always below the fraction bar, and shows how many pieces the whole has been divided into.
The sum is the answer to an addition problem.
There is no multiplication or subtraction used in this equation. -
Identify the statements that accurately describe tenths and hundredths.
Hints$\mathbf{\frac{1}{10}}$ is one piece from a group of 10.
$\mathbf{\frac{1}{100}}$ is one piece from a group of 100.
There are three correct answers.
Solution- A tenth represents one part of a whole, divided into 10 equal pieces.
- A hundredth represents one part of a whole divided into 100 equal parts.
- One hundredth can by written as a fraction by writing 1 as the numerator and 100 as the denominator.
- In a fraction, the numerator, or number on top, shows how many of something there is. So the fraction one tenth must be written as $\mathbf{\frac{1}{10}}$.
- 10 and 100 can both be divided by 2's, 5's and 10's, but not by 7.
-
Identify the correct order or steps to solve.
HintsIn order to add tenths and hundredths, the denominator must first be the same. In the fraction $\frac{1}{10}$, 10 is the denominator.
To make common denominators, the best strategy is to multiply smaller numbers, like 10, untill they equal the larger denominator in the other fraction.
$\mathbf{\frac{50}{100}}$ can be simplified to a smaller fraction by dividing both the numerator and denominator by 50.
SolutionTo add tenths and hundredths,
- Check if the two fractions have like denominators.
- If the fractions do NOT have like denominators, multiply the denominator of the smaller fraction until it is the same. Multiply the numerator by the same.
- Once all fractions have the same denominator, add the equivalent fractions together to get the sum.
- Simplify by dividing the numerator and denominator of the sum by a common denominator, if possible.
-
Match each addition expression with the correct sum.
Hints30 ÷ 10 = 3
100 ÷ 10 = 1070 ÷ 10 = 7
100 ÷ 10 = 1020 ÷ 20 = 1
100 ÷ 20 = 50SolutionProblem 1
- $\frac{10}{100}$ + $\frac{2}{10}$ = ?
- $\frac{2}{10}$ x $\frac{1}{10}$ = $\frac{20}{100}$
- $\frac{10}{100}$ + $\frac{20}{100}$ = $\frac{30}{100}$
- $\frac{30}{100}$ ÷ $\frac{10}{10}$ = $\frac{3}{10}$
- $\frac{20}{100}$ + $\frac{5}{10}$ = ?
- $\frac{5}{10}$ x $\frac{10}{10}$ = $\frac{50}{100}$
- $\frac{20}{100}$ + $\frac{50}{100}$ = $\frac{70}{100}$
- $\frac{70}{100}$ ÷ $\frac{10}{10}$ = $\frac{7}{10}$
- $\frac{7}{100}$ + $\frac{10}{100}$ = $\frac{17}{100}$
- $\frac{10}{100}$ + $\frac{10}{100}$ = ?
- $\frac{10}{100}$ + $\frac{10}{100}$ = $\frac{20}{100}$
- $\frac{20}{100}$ ÷ $\frac{20}{20}$ = $\frac{1}{50}$
-
Calculate the sum of the equation.
HintsThe first step to solve the problem is to identify the unknown amount with a question mark (?).
In order to add tenths and hundreds, you first have to create like denominators using multiplication. Multiply BOTH the numerator (above) and denominator (below).
Like denominators: $\mathbf{\frac{10}{20}}$ + $\mathbf{\frac{2}{20}}$
Different denominators: $\mathbf{\frac{1}{50}}$ + $\mathbf{\frac{1}{10}}$
Once you have like denominators, you can add your fractions to find the sum. Only add the numerators! (The number above).
$\mathbf{\frac{30}{100}}$ + $\mathbf{\frac{20}{100}}$ = ?
Once you have added your fractions and have the sum, check if the sum can be simplified, or made smaller, using division. Divide BOTH the numerator (above) and denominator (below).
$\mathbf{\frac{50}{100}}$ ÷ $\mathbf{\frac{50}{50}}$ = ?
Solution- $\frac{3}{100}$ + $\frac{2}{10}$ = ?
- $\frac{2}{10}$ x $\frac{10}{10}$ = $\frac{20}{100}$
- $\frac{30}{100}$ + $\frac{20}{100}$ = $\frac{50}{100}$
- $\frac{50}{100}$ ÷ $\frac{50}{50}$ = $\frac{1}{2}$
-
Calculate the sum of the equations.
HintsYou will need to first find like denominators before you can solve these equations.
For the equation $\frac{2}{30}$ + $\frac{1}{3}$, the common denominator is 3. How many times must you multiply 3 to equal 30?
Don't forget to simplify fractions when you can!
Example: $\frac{2}{10}$ can be simplified to $\frac{1}{5}$ by dividing by 2.A piece of scrap paper to write out each step is recommended for this problem!
SolutionProblem 1
- $\frac{1}{4}$ + $\frac{1}{40}$ = ?
- $\frac{10}{40}$ + $\frac{1}{40}$ = ?
- $\frac{10}{40}$ + $\frac{1}{40}$ = $\frac{11}{40}$
- $\frac{11}{40}$ cannot be simplified.
- $\frac{2}{5}$ + $\frac{2}{50}$ = ?
- $\frac{20}{50}$ + $\frac{2}{50}$ = ?
- $\frac{20}{50}$ + $\frac{2}{50}$ = $\frac{22}{50}$
- $\frac{22}{50}$ is equivalant to $\frac{11}{25}$ (divide by 2).
- $\frac{2}{30}$ + $\frac{1}{3}$ = ?
- $\frac{2}{30}$ + $\frac{10}{30}$ = ?
- $\frac{2}{30}$ + $\frac{10}{30}$ = $\frac{12}{30}$
- $\frac{12}{30}$ is equivalant to $\frac{6}{15}$ (divide by 2).
- $\frac{1}{2}$ + $\frac{3}{10}$ = ?
- $\frac{5}{10}$ + $\frac{3}{10}$ = ?
- $\frac{5}{10}$ + $\frac{3}{10}$ = $\frac{8}{10}$
- $\frac{8}{10}$ is equivalant to $\frac{4}{5}$ (divide by 2).
Adding Fractions on a Number Line
Adding Fractions with Like Denominators
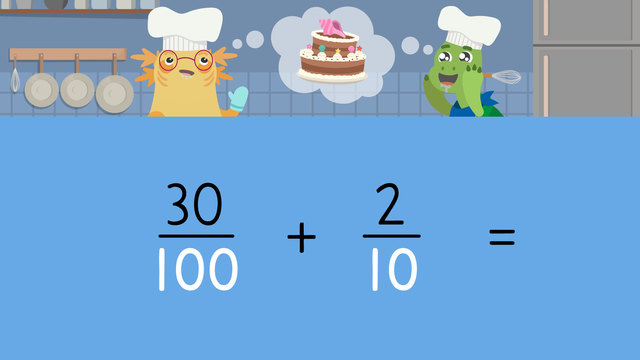
Adding Tenths and Hundredths

Adding Tenths and Hundredths — Let's Practice!
Adding and Subtracting Mixed Numbers
Adding Fractions on a Number Line — Let's Practice!

Adding Fractions with Unlike Denominators
Adding Mixed Numbers with Unlike Denominators














