Adding and Subtracting Mixed Numbers

Basics on the topic Adding and Subtracting Mixed Numbers
Mixed Numbers – Adding and Subtracting
Have you ever tried making slime at home? It is a lot of fun!
For the special slime we want to make today, the recipe is difficult to read, as it contains mixed numbers. In order to figure out how much to use of each ingredient, we need to learn and practice adding and subtracting mixed numbers. Not to worry – the following text teaches us everything we need to know.
Steps to Adding and Subtracting Mixed Numbers
A mixed number is a combination of a whole number and a fraction. When you practice adding and subtracting mixed numbers with like denominators, you can follow these three steps:
| Step # | What to do |
|---|---|
| 1 | Add or subtract the whole numbers. |
| 2 | Add or subtract the fractions. |
| 3 | Simplify your answer if you need to. |
Adding and Subtracting Mixed Numbers – Examples
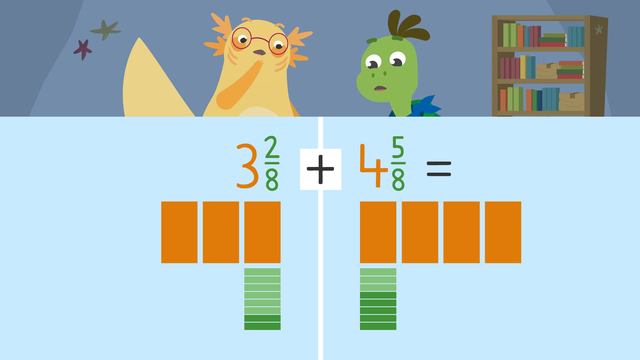
The first ingredient on the recipe is glue. It says to add three and two-eighths plus four and five-eighths. What is that in total? Let’s start by adding three and two-eighths and four and five-eighths.
First, we need to find the sum of the whole numbers. That means, we are adding three and four first to get the sum of seven.
Next, we find the sum of the fractions.
Remember: When adding and subtracting fractions with common denominators, we simply add or subtract the numerators and the denominators stay the same. Here, this means two-eighths plus five-eighths equals seven-eighths.
Our last step is to simplify our answer if we need to. A fraction is in simplest form when the numerator and denominator have no common factors other than one. Since seven and seven-eighths is in simplest form we can skip this step.
What is the next ingredient on the slime recipe? Now, we have to add five and three-fourths minus four and one-fourth of baking soda. So let’s practice subtracting mixed numbers by calculating five and three-fourths minus four and one-fourth.
First, we need to find the difference of the whole numbers. That means, we are subtracting five and four first to get the difference of one.
Next, we find the difference of the fractions. Three-fourths minus one-fourth equals two-fourths.
Our last step is again to simplify our answer if we need to. The numerator and the denominator have the common factor of two, which means it can be simplified to one-half.
How to Add and Subtract Mixed Numbers – Summary
Remember to follow the three steps below whenever you add and subtract mixed numbers with like denominators.
- Step 1: Find the sum or the difference of the whole numbers.
- Step 2: Find the sum or the difference of the fractions.
- Step 3: Simplify your answer if possible.
The last step in our recipe is to add one and one-third plus two and two-thirds of contact lense solution. Can you calculate how much that is in total?
The answer is... four! Well done.
If you would like to practice some more to optimize your slime, take a look at the exercises and worksheets about adding and subtracting mixed numbers. Enjoy!
Transcript Adding and Subtracting Mixed Numbers
Axel and Tank are having a lazy day. Tank decides he wants to read a book, but what is this? [curious/surprised] Looks like some kind of recipe...very mysterious! In order to figure out what the recipe makes, Tank and Axel need to... [title] "add and subtract mixed numbers" so they know how much of each ingredient to use. A mixed number is a combination of a whole number and a fraction. We can add or subtract mixed numbers using three steps. The first step is to add or subtract the whole numbers. The second step is to add or subtract the fractions. The third step is to simplify your answer if you need to. Let's see how many containers of glue Axel and Tank need. In order to do that, we need to ADD three and two-eighths and four and five-eighths. First, we need to find the sum of the whole numbers. That means, we are adding three (...) and four first...what is the sum of three PLUS four? (...) The sum of three and four is seven. Next, we find the sum of the fractions. Remember, when we add or subtract fractions with COMMON denominators... we simply add or subtract the NUMERATORS (...) and the DENOMINATORS stay the same Two-eighths (...) plus five-eighths equals (...) seven-eights. Our last step is to simplify our answer if we need to. A fraction is in simplest form when the numerator and denominator have no common factors other than one. This is true for the fraction seven-eighths, so they need "seven and seven-eighths" containers of glue. Now, let's help them calculate how many containers of baking soda they need. In order to do that, we need to SUBTRACT "five and three-fourths and four and one-fourth". First, we need to find the difference of the whole numbers. So, what is the difference of the whole numbers when you subtract? When we subtract the whole numbers five (...) and four(...) the difference is (...) "one". Next, we subtract the fractions. What is the difference of the fractions three-fourths (...) and one-fourth? Since the denominators stay the same, we only subtract three MINUS one. Three MINUS one is two which gives us the final answer "two-fourths". Our last step is to simplify our answer if we need to. Can we simplify the fraction two-fourths?
The numerator and the denominator have the common factor of two, which means it CAN be simplified to "one-half". Axel and Tank need one and one-half containers of baking soda for the recipe. Lastly, let's help them calculate how many containers of contact lens solution they need. In order to do that, we need to ADD "one and one-third (...) and two and two-thirds". First, can you find the sum of the whole numbers by adding? The sum of one (...) plus two(...) is "three". Next, we add the fractions. What is the sum of the fractions? The sum of one-third(...) plus two thirds(...) is "three-thirds". Our last step is to simplify our answer if we need to. Can we simplify the fraction three-thirds? Since we have all three parts of our whole(...)we can rewrite three-thirds as one whole. Now we add three PLUS one which gives us "four". Axel and Tank need four containers of contact lens solution for the recipe. Remember (...), you can add or subtract mixed numbers with common denominators by following three steps. The first step is to "add or subtract the whole numbers". The second step is to "add or subtract the fractions". The third step is to "simplify your answer if you need to". Luckily, Axel and Tank had enough of each ingredient on hand. Let's see how the recipe turned out!
Adding and Subtracting Mixed Numbers exercise
-
Can you find the mixed numbers?
HintsIs it made up of a whole number and a fraction?
Remember, a mixed number is made up of a whole number and a fraction.
SolutionThese are the mixed numbers! Remember, a mixed number is made up of a whole number and a fraction.
Not mixed numbers
5 and 13 are whole numbers.
$\frac{9}{10}$ and $\frac{5}{7}$ are fractions.
-
Can you sequence the number sentence correctly?
HintsThis is a subtraction problem so the order is important.
Start with the biggest number.
Have a look at this fraction. If you divide both the numerator and the denominator by 2, what do you get?
Remember, answers may be simplified.
SolutionThis is how the number sentence should read.
First of all we subtract the whole numbers so 3 - 1 = 2.
We then subtract the fractions so $\frac{3}{4}$ - $\frac{1}{4}$ = $\frac{2}{4}$.
We then simplify if we need to which in this case we can. $\frac{2}{4}$ can be simplified to $\frac{1}{2}$ by dividing both the numerator and the denominator by two.
We then put the whole number and the fraction together to get our answer of 2$\frac{1}{2}$.
-
Can you find out how much of each ingredient Axel and Tank need to make gloop?
HintsCan it be simplified?
Add or subtract the whole numbers first.
Don't forget to double check if it is an addition or subtraction problem.
Add or subtract the fractions next.
SolutionThese are the correct answers. Remember to:
- Check whether it is an addition or subtraction problem.
- Add or subtract the whole numbers first.
- Add or subtract the fractions next.
- Simplify if you can.
-
Can you find the equivalent fractions?
HintsRemember, you always divide the numerator and the denominator by the same number.
Think about common factors.
In this example we can simplify $\frac{3}{6}$ to $\frac{1}{2}$ by dividing both the numerator and denominator by 3.
What do you get if you half the denominator on the top row? Or divide it by 3?
SolutionIn the example above both the numerator and the denominator have been divided by two to simplify the fraction.
You need to divide the denominator and the numerator by the same number to simplify the fraction. This may be by two or by three or by another number.
__________________________________________________________________
Using the information above, the answers to the other problems are:
- $5\frac{8}{10}$ = $5\frac{4}{5}$ - both divided by two.
- $5\frac{3}{9}$ = $5\frac{1}{3}$ - both divided by three.
- $5\frac{12}{16}$ = $5\frac{3}{4}$ - both divided by four.
-
Can you find out how much shaving foam Axel and Tank need to make more slime?
HintsRemember to add the whole numbers first.
Add the fractions next.
When the denominators are the same, we only need to add the numerators.
SolutionIf we add the whole numbers first we get 3.
Adding the fractions next gives us $\frac{2}{3}$; we cannot simplify this any further.
-
Can you check Axel and Tank's alternative recipe for slime?
HintsRemember to add or subtract the whole numbers first.
Add or subtract the fractions next.
Can the fraction be simplified?
Solution- The first number sentence was incorrect.
3 + 6 = 9
$\frac{5}{8}$ + $\frac{1}{8}$ = $\frac{6}{8}$ which can be simplified to $\frac{3}{4}$.
We put the whole number and the fraction together to get the answer.
- The second problem was correct!
$\frac{7}{9}$ + $\frac{2}{9}$ = 1.
8 + 1 = 9.
- The third number sentence was also incorrect.
10 - 7 = 3.
$\frac{6}{7}$ - $\frac{2}{7}$ = $\frac{4}{7}$.
This cannot be simplified further so put the whole number and the fraction together to get the answer.
- The fourth number sentence was correct!
$\frac{7}{8}$ - $\frac{3}{8}$ = $\frac{4}{8}$ which can be simplified to $\frac{1}{2}$.
Put the whole number and the fraction together to get the answer.
Adding Fractions on a Number Line
Adding Fractions with Like Denominators
Adding Tenths and Hundredths

Adding Tenths and Hundredths — Let's Practice!

Adding and Subtracting Mixed Numbers
Adding Fractions on a Number Line — Let's Practice!

Adding Fractions with Unlike Denominators
Adding Mixed Numbers with Unlike Denominators














