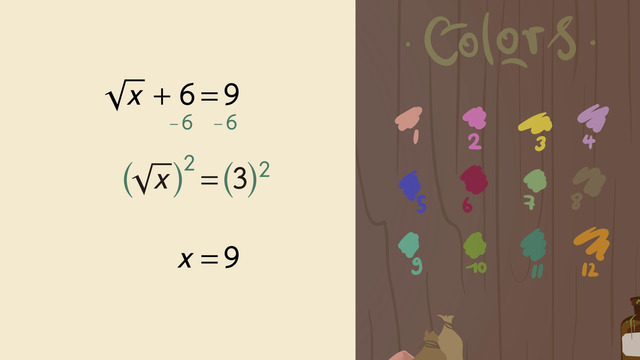The Distance Formula

Basics on the topic The Distance Formula
The distance formula is a formula used to find the distance between two distinct points on a plane. The formula was derived from the Pythagorean theorem, which states that for any right triangle, the square of the hypotenuse is equal to the sum of the square of the two legs.
Finding the distance between two distinct points on a plane is the same as finding the hypotenuse of a right triangle. From this perspective, the distance formula states that the distance of two distinct points on a plane is equal to the square root of the sum of the square of the rise and run.
The distance formula comes with some uses in everyday life. It can be used as a strategy for easy navigation and distance estimation. For example, if you want to estimate the distance of two places on a map, simply get the coordinate of the two places and apply the formula. Or when a pilot wants to know the distance of an incoming plane and his plane, he can use the plane radar and find the coordinates of the two planes and then apply the formula.
Use coordinates to prove simple geometric theorems algebraically
CCSS.MATH.CONTENT.HSG.GPE.B.7
Transcript The Distance Formula
Deep in the Amazonian jungle, Carlos lives with his family in a teeny-tiny village. Carlos likes most things about his village, but he has to wake up at the crack of dawn if he wants to be at school on time. It’s not so much that his school is so far away, but there’s a huge canyon between the village and the school, so Carlos must walk around the canyon to get to his school. To make his journey faster, Carlos has a great idea. But to make sure his idea will work he’ll need to use the Distance Formula.
Take a look at this map The scale's in yards. Here’s the path that Carlos usually walks to go to school, around this side of the canyon, across the bridge, and then along the other side of the canyon. It takes Carlos about 2 hours to walk to school every day. So, what's Carlos' great idea? He wants to build a zip line to go right across the canyon, allowing him to get to school in a fraction of the time! But he doesn't have any rope. What can he do? In a stroke of genius, Carlos decides to use the rope from his mom's clothesline. There are just two problems with this plan: the clothesline is only 350 yards long. Will that be enough? And what will his mom say about him using the rope from the clothesline to build the zip line?
Using the Pythagorean Theorem to Calculate the Distance
To answer the first question, he needs to calculate the distance between these two points. As for Carlos' mom and the missing clothesline? Only time will tell...
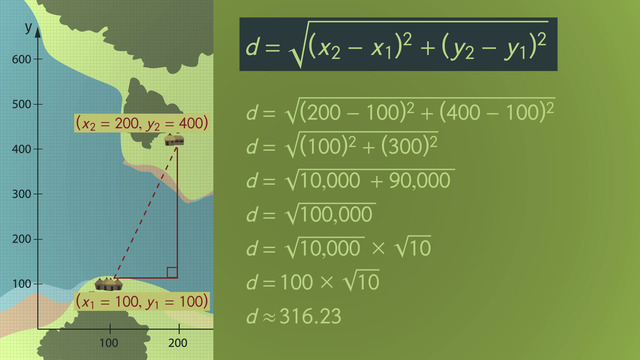
We can't help Carlos out with his mom, but we can help him solve his little math problem. To find the distance between any two known points in a coordinate plane, first construct a right triangle. Then, modify the Pythagorean Theorem to solve for the unknown distance. Notice how we replaced 'a' and 'b' with the quantities 'x'-two minus 'x'-one and 'y'-two minus 'y'-one, respectively. Since 'c' is the distance we want to know, we'll now call this variable 'd'.
After taking the square roots of both sides of the equation, we're left with the Distance Formula. The location of Carlos' village is at the ordered pair one hundred, one hundred and the location of his school is at the ordered pair two hundred, four hundred. Carlos' home will be point 1 and his school will be point 2. Now, using the known points, we can replace the variables in the expression and solve for the distance Now that there are no more variables, we can finish this off with PEMDAS to get the distance. To get across the canyon, the zip line only needs to be approximately 316.23 yards...so Carlos has enough rope!
He's really excited to use the zip line for the first time, AND he was even able to sleep two hours longer than usual.
There he goes. Whe! Oh man, now Carlos knows a bit more about the villagers than he wanted.
The Distance Formula exercise
-
Explain how to calculate the distance between two points.
HintsThe Pythagorean theorem states that the sum of the squares of the legs of any right triangle is the same as the square of the hypotenuse.
In the picture above, the lengths of both legs are given by the difference of the coordinates of the two points.
We don't want to know the squared distance.
SolutionTo determine the distance between two given points, $(x_1,y_1)$ and $(x_2,y_2)$, in a coordinate plane we first draw a right angle.
Then we use the Pythagorean theorem to get
$(x_2-x_1)^2+(y_2-y_1)^2=c^2$,
where $c$ is the length of the hypotenuse.
Because the length of the hypotenuse is the desired distance, we replace it by $d$:
$(x_2-x_1)^2+(y_2-y_1)^2=d^2$.
Lastly, we take the square root on both sides and change the sides to get the distance formula
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
-
Calculate the distance from Carlos' village to his school.
HintsHere you see the distance formula for two points in a coordinate plane.
You get the points by just looking at the coordinate plane on the map pictured above.
For Carlos' village:
- Draw a line parallel to the $x$-axis passing this point. The $y$-coordinate is the intersection of this line and the $y$-axis.
- Draw a line parallel to the $y$-axis passing this point. The $x$-coordinate is the intersection of this line and the $x$-axis.
PEMDAS means the order of operations:
- Paranthesis
- Exponent
- Multiplication
- Division
- Addition
- Subtraction
SolutionThe coordinates of Carlos' village as well as his school are:
- Home: $(100,100)$
- School: $(200,400)$
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$,
where, in our situation, we have that:
- $x_2=200$
- $x_1=100$
- $y_2=400$
- $y_1=100$
$d=\sqrt{(200-100)^2+(400-100)^2}$.
Using PEMDAS, we get
$d=\sqrt{(100)^2+(300)^2}=\sqrt{10000+90000}=\sqrt{100000}$.
We can simplify this expression to get
$d=100\sqrt{10}\approx316.23$.
-
Connect the ordered pairs with the right formula.
HintsPay attention to the correct order of the points.
Just check the exponents.
Here you see an example of using the distance formula.
So we have $d=\sqrt{(56-12)^2+(78-34)^2}$.
SolutionThe distance between two points is the square root of the sum of the squares of the differences of the coordinates:
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Let's practice it with a few pairs of points:
The distance between $(10,20)$ and $(30,40)$ is
$d=\sqrt{(30-10)^2+(40-20)^2}$.
Pay attention to the order: $(10,20)$ and $(40,30)$ leads to
$d=\sqrt{(40-10)^2+(30-20)^2}$.
It looks quite similar, but it's totally different.
The distance between $(40,20)$ and $(10,50)$ is
$d=\sqrt{(10-40)^2+(50-20)^2}$,
while the distance between $(40,20)$ and $(50,10)$ is
$d=\sqrt{(50-40)^2+(10-20)^2}$.
-
Determine the distance.
HintsUse the distance formula for two points in a coordinate plane:
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
If you have to round to the nearest hundredth, you just have to look at the third position after the decimal: if this position is less or equal $4$ then round down, otherwise round up.
Here are two examples for rounding decimals:
SolutionThe point representing Carlos' location is $(100,100)$ and the point representing where his friend lives is $(150,300)$.
We use the distance formula for two points in a coordinate plane:
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$,
with the given coordinates above. So we put them into this formula to get
$d=\sqrt{(150-100)^2+(300-100)^2}$.
Using PEMDAS, we get
$d=\sqrt{(50)^2+(200)^2}=\sqrt{2500+40000}=\sqrt{42500}$.
We can write this result as
$d=\sqrt{2500\times17}=50\sqrt{17}$,
or as a rounded decimal
$d\approx206.16$.
-
Find the right distance formula.
HintsHere you see a right triangle with the points $(x_1,y_1)$ and $(x_2,y_2)$.
Use the Pythagorean property:
The sum of the squares of the legs of any right triangle is the same as the square of the hypotenuse.
The distance is the length of the hypotenuse.
SolutionTwo points, $(x_1,y_1)$ as well as $(x_2,y_2)$, of a right triangle are given.
With the Pythagorean theorem, we get
$(x_2-x_1)^2+(y_2-y_1)^2=c^2$,
where $c$ is the length of the hypotenuse and $|x_2-x_1|$ and $|y_2-y_1|$ the lengths of the legs.
Because the length of the hypotenuse is the desired distance, we replace it by $d$:
$(x_2-x_1)^2+(y_2-y_1)^2=d^2$.
Lastly, we take the square root on both sides and change the sides to get the distance formula
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
-
Examine the distances of the given points.
HintsUse the distance formula:
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Here you see an example for the calculation of the distance of the two points $(10,40)$ and $(40,20)$.
Be careful with the order of the coordinates.
SolutionThe distance between two points is given as the square root of the sum of the squares of the differences of the coordinates:
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Let's practice the calculation of the distance for a few pairs of points:
$(10,20)$ and $(30,40)$ gives
$\begin{array}{rcl} d&=&~\sqrt{(30-10)^2+(40-20)^2}\\ &=&~\sqrt{(20)^2+(20)^2}\\ &=&~\sqrt{800}=20\sqrt2 \end{array}$
Pay attention to the order of the coordinates: $(10,20)$ and $(40,30)$ leads to
$\begin{array}{rcl} d&=&~\sqrt{(40-10)^2+(30-20)^2}\\ &=&~\sqrt{(30)^2+(10)^2}\\ &=&~\sqrt{1000}=10\sqrt{10} \end{array}$
So you see, it's very important to be careful with the order of the coordinates. Those calculations look quite similar, but the result is totally different.
The distance between $(10,30)$ and $(30,30)$ is
$\begin{array}{rcl} d&=&~\sqrt{(30-10)^2+(30-30)^2}\\ &=&~\sqrt{(20)^2}\\ &=&~20 \end{array}$
Lastly, the distance between $(40,40)$ and $(10,90)$ is
$\begin{array}{rcl} d&=&~\sqrt{(10-40)^2+(90-40)^2}\\ &=&~\sqrt{(-30)^2+(50)^2}\\ &=&~\sqrt{2500}=50 \end{array}$