Radical Expressions / Equations

Content

• Introduction
• Simplifying Radical Expressions
• Solving Radical Equations
• Adding Radical Expressions
• Subtracting Radical Expressions
• Multiplying Radical Eqxpression
• Dividing Radical Expressions
• Distance Formula
• Midpoint Formula

Introduction

A radical expression is any expression that contains a radical symbol. Radical symbols are use to find the square roots, cubic root, and higher.

Simplifying Radical Expressions

To make simplifying radical expressions easier, learn the radical properties. Remember, numbers under the radical may not be less than zero because the squared, cubed, and higher roots of negative numbers are not real numbers.

Product Property of Radicals: $\sqrt{x} \times \sqrt{y}=\sqrt{xy}$

Quotient Property of Radicals: $\sqrt{\frac{x}{y}} =\frac{\sqrt{x}}{\sqrt{y}}$

To make radical properties easier to understand, substitute perfect squares for the variables in the properties.

$\begin{align} \sqrt{16}\times \sqrt{81}&= \sqrt{16\times81}\\ 4 \times9&= \sqrt{196}\\ 36&=36 \end{align}$

$\begin{align} \sqrt{\frac{16}{4}} &=\frac{\sqrt{16}}{\sqrt{4}}\\ \sqrt{4}&=\frac{4}{2}\\ 2&=2 \end{align}$

Radicals are not allowed in the denominator of fractions. To undo the radical, rationalize the denominator.

$\sqrt{\frac{x}{y}} =\frac{\sqrt{x}}{\sqrt{y}}=\frac{\sqrt{x}}{\sqrt{y}}\times\frac{\sqrt{y}}{\sqrt{y}} =\frac{\sqrt{xy}}{\sqrt{y^{2}}}=\frac{\sqrt{xy}}{y}$

When you rationalize the denominator, the radical cancels out.

$\frac{3}{\sqrt{5}} =\frac{3}{\sqrt{5}}\times\frac{\sqrt{5}}{\sqrt{5}} =\frac{3\sqrt{5}}{\sqrt{5^{2}}}=\frac{3\sqrt{5}}{5}$

Solving Radical Equations

Just like exponents, you can add, subtract, multiply, and divide expressions containing radicals to calculate solutions.

Adding Radical Expressions

To add expressions, if possible, simplify to remove the radical.

This expression is the sum of perfect squares. Simplify each perfect square then sum.

$\sqrt{36} + \sqrt{25} = 6 + 5 = 11$

Subtracting Radical Expressions

If you can’t remove the radical, write the difference as a radical expression.

$\sqrt{64}-\sqrt{24}=8-\sqrt{4\times6}= 8-\sqrt{4}\times\sqrt{6}=8-2\sqrt{6}$

Multiplying Radical Eqxpression

Remember to use the product rule when multiplying radical expressions.

For this problem, the product contains a radical. Use your calculator to determine the decimal answer, if needed.

$\sqrt{9}\times\sqrt{16}\times\sqrt{30}=3\times 4\times\sqrt{30}=12\times\sqrt{30}=12\sqrt{30}=65.73$

Dividing Radical Expressions

When simplifying expressions, apply the quotient rule.

This problem is the quotient of two perfect squares.

$\sqrt{\frac{9}{16}}=\frac{\sqrt{9}}{\sqrt{16}}=\frac{3}{4}$

Distance Formula

To find the distance between two points on a graph, we use the distance formula.

Distance Formula

$d=\sqrt{\left( x_2-x_1\right) ^{2}+\left( y_2-y_1\right) ^{2}}$

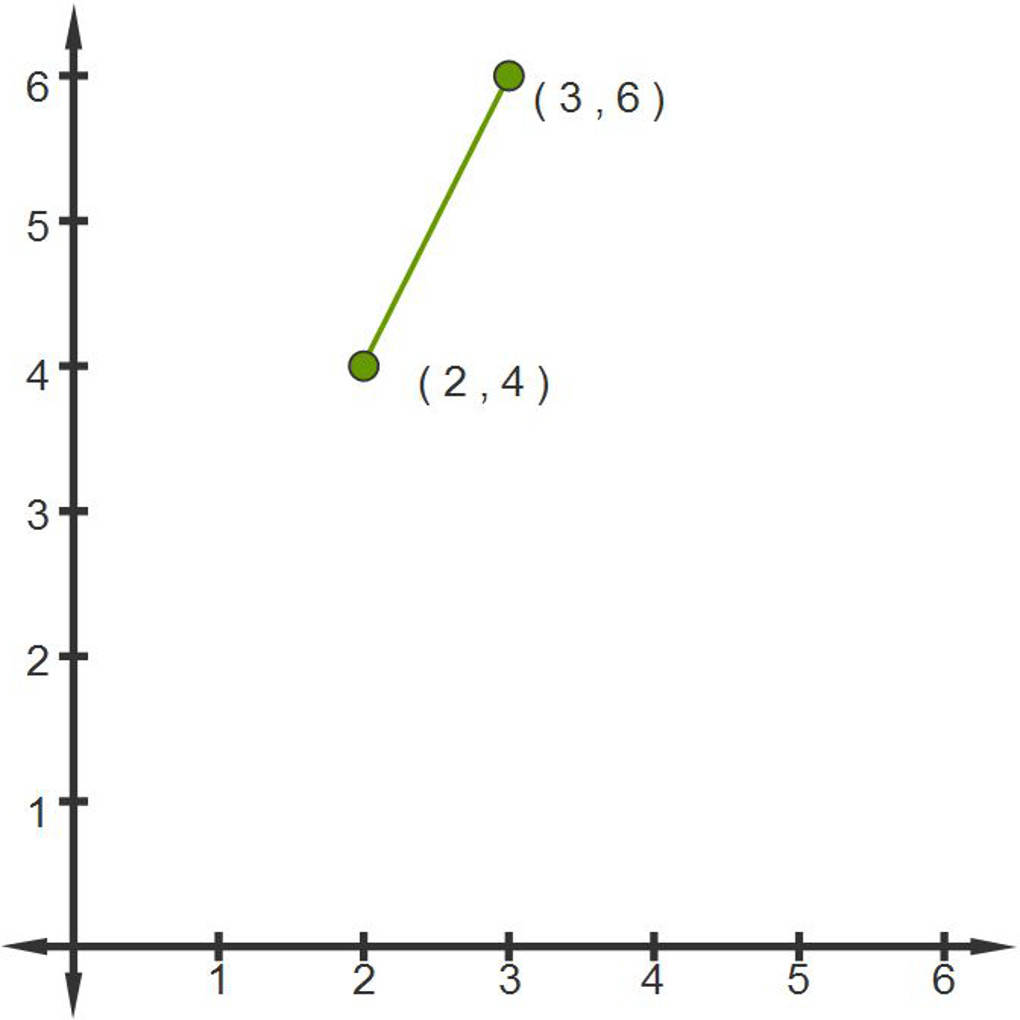
Find the distance of the two points shown on the graph.

Use the distance formula to solve. Apply what you know about exponents and radicals to determine the answer.

$\begin{align} d&=\sqrt{ \left(3 -2\right)^{2}+\left(6 -4\right)^{2}}\\ d&=\sqrt{ \left(1\right)^{2}+\left(2\right)^{2}}\\ d&=\sqrt{ 1 +4}\\ d&=\sqrt{5} \end{align}$

The distance between the two points is equal to $\sqrt{5}.

Midpoint Formula

The midpoint formula is used to find the exact midpoint between two points on a graph.

Midpoint Formula

$\left(\frac{x_1+x_2}{2},\frac{y_1 +y_2}{2}\right)$

Find the midpoint of the two points shown on the graph above, $(2,4)$ and $(3, 6)$

When you enter the x and y-values into the equation, be careful not to mix up the numbers.

$\left(\frac{2+3}{2},\frac{4 +6}{2}\right)=\left(\frac{5}{2},\frac{10}{2}\right)=\left(2.5,5\right)$

The midpoint is at $(2.5, 5)$