Rationalize the Denominator


Basics on the topic Rationalize the Denominator
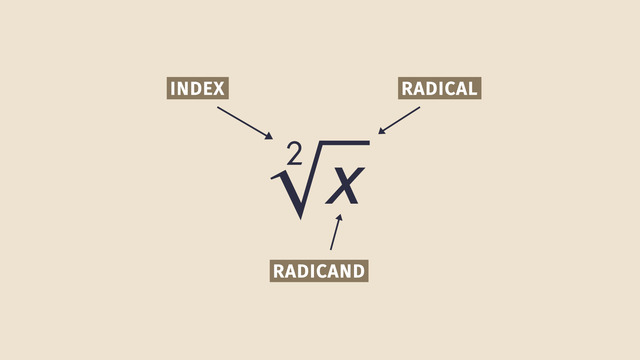
An important rule when simplifying radical expressions is that there must be no radical sign in the denominator of the expression. Removing the radical sign in the denominator of an expression is known as rationalizing the denominator.
There are two very important points to remember when rationalizing the denominator. First, the product property of square roots, which states that √a * √b = √ab. This is important when removing a square root of a number, like √a, in the denominator. We can multiply the expression with a fraction equal to one, like √b/√b, so that the denominator product √ab can be simplified, if ab is a perfect square.
Second, the conjugate, which can be obtained by multiplying the second term of a binomial by -1. This is what we use when we have a term, like (a + √b) in the denominator. We multiply the expression with a fraction equal to 1, specifically (a - √b)/(a - √b), so that after multiplying, we will have a2 + a√b - a√b - √(b2), where the middle terms cancel each other out.
You will definitely find that rationalizing the denominator is an easy tool in simplifying expressions, especially when you master these two points.
Expressions and Equations Work with radicals and integer exponents.
CCSS.MATH.CONTENT.8.EE.A.2
Transcript Rationalize the Denominator
Meet Mellow Mike. He’s a happy fellow and quite content with his tranquil life living on the first floor of a two-story house except for one problem, his roommate, Radical Ruben. Mellow Mike wants Ruben to move out and go away because Ruben is way too radical for Mike’s taste. The chaos Ruben causes disrupts the harmony of their shared space. Dealing with Reuben is a lot like Rationalizing the Denominator in radical expressions with fractions. How, you ask? Let me show you.
Simplifying Radical Equations
When you simplify radical expressions in fractions, just like Mike, you want to get rid of the radical living on the first floor of the fraction or rather, in the denominator. Take a look at this fraction: two over root 3. How can we make root 3 go away? To solve this problem, let’s first review the Product Property of Square Roots. The property states the square root of ‘a’ times the square root of ‘b’ is equal to the square root of the product ‘ab.’
Let’s look at an example, the square root of 3 times the square root of 3 is the same as the square root of the product of 3 and 3 which is the same as the square root of 9 which is a perfect square - and equal to 3. How can we use this information to get rid of root 3 in the denominator of this fraction? Multiply the fraction by another fraction that is equal to one and comprised of the radical from the denominator - in this case, root 3 over root 3.
Lookey there, that made the radical in the denominator disappear! Of course, now we have a radical upstairs in the numerator, but we can live with that. But, if there’s a factor joined with the radical, what then? No problem, follow the same steps as before. Multiply the fraction by the new fraction equal to 1 that is comprised of the radical number from the denominator. Again, the radical moves from the downstairs to the upstairs, and that’s okay. Finally, if possible, simplify the fraction.
Sum in the denominator
What if the situation is more complicated? There’s a sum or difference with a radical in the denominator. Is this an impossible situation? No, just follow these steps. First, instead of multiplying the fraction by a new fraction equal to 1 comprised of the radical from the denominator, for this situation make the new fraction equal to 1 from the conjugate of the denominator. The conjugate?! What’s that you ask? In algebra, to write a conjugate, just multiply the second term of the second binomial by negative 1.
For example, for a + b, the conjugate is a – b. And just to help you understand why we do this, foil the two binomials the product is a-squared minus b-squared is equal to the difference of two squares because the two middle terms cancel each other out. Okay, so let's write a fraction equal to 1 that is comprised of the conjugate of 5 minus the square root of 7. Do the mathmand we're left with 15 plus 3 root 7 all divided by 18.
Looking at the constants and coefficients in each term, we find that they all have something in common: they're all divisible by 3. So we can factor out a 3 from the numerator and denominator and we're left with 5 plus the square root of 7 over 6. By multiplying the denominator by its conjugate, we're able to make the radical in the denominator disappear. It’s not magic, just math!
So just like in the example problems, Mellow Mike also got rid of his radical. I think you already know where he moved. Luckily for Radical Reuben, unlike Mellow Mike, Dancing Donna from the 2nd floor likes to raise the roof.
Rationalize the Denominator exercise
-
Simplify $\frac{2}{\sqrt3}$ as well as $\frac2{4\sqrt3}$.
HintsUpstairs stands for the numerator and downstairs stands for the denominator.
To get rid of the $\sqrt 2$ in the denominator on the lefthand side of the example pictured, the numerator as well as the denominator must be multiplied by $\sqrt 2$.
Keep the notation in mind.
SolutionWe have to multiply the fraction with another fraction equal to $1$ to get rid of a radical in the denominator.
Let's have a look at the following example: $\frac2{\sqrt3}$.
To get rid of $\sqrt3$ in the denominator, we use the following property:
- $\sqrt a\times \sqrt b=\sqrt{a\times b}$, and thus
- $\sqrt 3\times \sqrt 3=\sqrt{3\times 3}=\sqrt9=3$
$\frac2{\sqrt3}=\frac2{\sqrt3}\times\frac{\sqrt3}{\sqrt3}=\frac{2\sqrt3}3$.
In a similar fashion, we proceed with the next example, $\frac2{4\sqrt3}$.
Here the denominator is a little bit more complicated. But don't worry we can do this as well:
- Expand the fraction by $\sqrt 3$.
- Simplify the terms in the numerator as well as in the denominator.
- Simplify the fraction if necessary.
$\begin{array}{rcl} \frac2{4\sqrt3}&=&~\frac2{4\sqrt3}\times\frac{\sqrt3}{\sqrt3}\\ &=&~\frac{2\sqrt 3}{4\sqrt3\times \sqrt 3}\\ &=&~\frac{2\sqrt 3}{12}\\ &=&~\frac{2\sqrt 3\div 2}{12\div 2}\\ &=&~\frac{\sqrt 3}{6} \end{array}$
-
Determine the steps for simplifying $\frac3{5-\sqrt7}$.
HintsExpanding the fraction means that the numerator as well as the denominator get multiplied by the same number or term.
The conjugate of the binomial $a+b$ is given by changing the sign of the second term to $a-b$.
If we multiply any binomial by its conjugate, we get the difference of two squares:
$(a+b)(a-b)=a^2-ab+ab-b^2=a^2-b^2$.
SolutionWe can't expand the fraction $\frac3{5-\sqrt7}$ just by a radical. This wouldn't work.
We have to expand the fraction by the conjugate of the denominator.
What's that? The conjugate of the binomial $a+b$ is given by changing the sign of the second term to $a-b$. Why should we do that?
If we multiply $a+b$ with the conjugate $a-b$, for example using the FOIL method, we get
$(a+b)(a-b)=a^2-ab+ab-b^2=a^2-b^2$,
the difference of two squares.
The conjugate of $5-\sqrt 7$ is $5+\sqrt 7$.
So we can start:
$\begin{array}{rcl} \frac3{5-\sqrt7}&=&~\frac3{5-\sqrt7}\times\frac{5+\sqrt 7}{5+\sqrt7}\\ &=&~\frac{3\times(5+\sqrt 7)}{(5-\sqrt7)\times(5+\sqrt 7)}\\ &=&~\frac{15+3\sqrt7}{25-7}\\ &=&~\frac{15+3\sqrt7}{18} \end{array}$
Because the numerator as well as the denominator have the factor $3$, we can simplify the fraction as follows
$\begin{array}{rcl} \frac3{5-\sqrt7}&=&~\frac{15+3\sqrt7}{18}\\ &=&~\frac{3(5+\sqrt7)}{3\times 6}\\ &=&~\frac{5+\sqrt7}{6} \end{array}$
-
Find the right factor to simplify the fraction.
HintsIf the denominator is a simple radical, like $\sqrt 2$ or $\sqrt 3$, expand the fraction by this radical.
If the denominator is the sum or the difference of any number and a radical, just expand the fraction by the conjugate of the denominator.
To get the conjugate of a binomial, change the sign of the second term of the binomial.
For example, the conjugate of $4+\sqrt2$ is $4-\sqrt2$.
SolutionThe main method for getting rid of a radical in the denominator is to find a factor with which we can expand the fraction.
If the denominator is a simple radical, like $\sqrt 2$ or $\sqrt 3$, we expand the fraction by this radical.
If the denominator is the sum or the difference of any number and a radical, we have to expand the fraction by the conjugate of the denominator. For this, we change the sign of the second term of the binomial.
So, let's try it:
- For $\frac{3}{\sqrt5}$ $\rightarrow$ we have to expand by $\sqrt5$
- For $\frac{5}{\sqrt3}$ $\rightarrow$ we have to expand by $\sqrt3$
- For $\frac{3}{3+\sqrt5}$ $\rightarrow$ we have to expand by $3-\sqrt5$
- For $\frac{5}{5-\sqrt3}$ $\rightarrow$ we have to expand by $5+\sqrt3$
-
Calculate the ratios.
HintsThe numerator as well as the denominator of the right-most fraction on the first line are conjugate to the denominator of the left-most faction on the first line.
We multiply two fractions by multiplying their numerators and their denominators together.
If the numerator as well as the denominator have the same factor, you can simplify the fraction by this factor.
The product of a binomial and its conjugate is the difference of two squares:
$(a+b)(a-b)=a^2-b^2$
SolutionLet's go through the calculation pictured to the right step-by-step:
- We see the minus sign in the denominator of the left-most fraction on the first line, and the number under the radical is missing. On the right-most side on the first line, we have a similar expression with a $\sqrt 5$. Here the operator is missing. In order for these fractions to be equal, we must have a plus sign on the righthand side and the number under the square root must be $5$ on the lefthand side.
- Because we expand the fraction by a fraction equal to $1$, the numerator as well as the denominator must be $1+\sqrt 5$.
- We multiply the numerators to get $4\times (1+\sqrt 5)=4+4\sqrt 5$. The denominator is the difference of two squares: $1^2-\sqrt5^2=1-5=-4$.
- Lastly, we can simplify the fraction by dividing the numerator as well as the denominator by $4$ to get the result: $\frac4{1-\sqrt5}=\frac{1+\sqrt5}{-1}=-(1+\sqrt5)=-1-\sqrt5$.
-
Define the conjugate of $a+b$ and its use.
HintsFor example, the conjugate of $5-\sqrt 7$ is $5+\sqrt7$.
Use the FOIL method to multiply:
$(5-\sqrt 7)(5+\sqrt7)=25-5\sqrt7+5\sqrt7-7=25-7=18$
Calculate $(a+b)(-a-b)$ as well as $(a+b)(a-b)$.
SolutionTo get rid of denominators like $5-\sqrt7$ we have to expand by the conjugate of the denominator.
So what is the conjugate of a binomial? The conjugate of the binomial $a+b$ is given by changing the sign of the second term to $a-b$; i.e. we multiply the second term in the binomial by $-1$.
Why should we do that?
If we multiply $a+b$ with the conjugate $a-b$, for example using the FOIL method, we get
$(a+b)(a-b)=a^2-ab+ab-b^2=a^2-b^2$,
the difference of two squares.
-
Simplify the given fractions.
HintsIf the denominator is a simple radical, like $\sqrt 2$ or $\sqrt 3$, just expand the fraction by this radical.
Otherwise expand by the conjugate of the binomial.
Change the sign of the second term of the binomial to get its conjugate.
For example, the conjugate of $a+b$ is $a-b$.
The product of any binomial with its conjugate is the difference of the its first term squared and its second term squared:
$(a+b)(a-b)=a^2-b^2$
SolutionThe main method for getting rid of a radical in the denominator is to find a factor with which we can expand the fraction with:
- If the denominator is a simple radical, like $\sqrt 2$ or $\sqrt 3$, we expand the fraction by this radical.
- If the denominator is the sum or the difference of any number and a radical, we have to expand the fraction by the conjugate of the denominator. For this, we change the sign of the second term of the binomial. The product of any binomial and its conjugate is the difference of the squares of the first and the second term of the binomial: $(a+b)(a-b)=a^2-b^2$
$\begin{array}{rcl} \begin{array}{rcl} \frac{3}{\sqrt5}&=&~\frac{3}{\sqrt5}\times\frac{\sqrt5}{\sqrt5}\\ &=&~\frac{3\sqrt5}{5} \end{array}\end{array}$
2.$~$ For $\frac{5}{\sqrt3}$, we have to expand it by $\sqrt3$:
$\begin{array}{rcl} \begin{array}{rcl} \frac{5}{\sqrt3}&=&~\frac{5}{\sqrt3}\times\frac{\sqrt3}{\sqrt3}\\ &=&~\frac{5\sqrt3}{3} \end{array}\end{array}$
3.$~$ For $\frac{3}{3+\sqrt5}$, we have to expand it by $3-\sqrt5$:
$\begin{array}{rcl} \frac{3}{3+\sqrt5}&=&~\frac{3}{3+\sqrt5}\times\frac{3-\sqrt5}{3-\sqrt5}\\ &=&~\frac{3(3-\sqrt5)}{(3+\sqrt5)(3-\sqrt5)}\\ &=&~\frac{9-3\sqrt5}{9-5}\\ &=&~\frac{9-3\sqrt5}{4} \end{array}$
4.$~$ For $\frac{5}{5-\sqrt3}$ $\rightarrow$, we have to expand it by $5+\sqrt3$:
$\begin{array}{rcl} \frac{5}{5-\sqrt3}&=&~\frac{5}{5-\sqrt3}\times\frac{5+\sqrt3}{5+\sqrt3}\\ &=&~\frac{5(5+\sqrt3)}{(5-\sqrt3)(5+\sqrt3)}\\ &=&~\frac{25+5\sqrt3}{25-9}\\ &=&~\frac{25+5\sqrt3}{16} \end{array}$