Solving Radical Equations
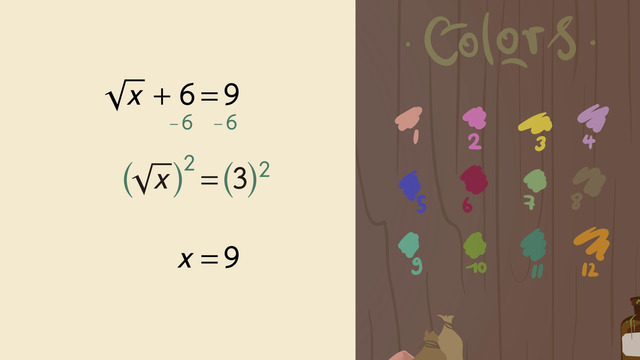

Basics on the topic Solving Radical Equations
Solving equations with radicals in them can seem quite intimidating at first glance. But upon deeper inspection, they can be relatively easy to solve as long as you follow a few guidelines:
One must be very familiar with the following checklist of steps when solving radical equations: 1. Isolate the term or terms with the radical 2. Square both sides of the equation 3. Solve for “x”.
In isolating the radical, it might be the case that two radicals occur in an equation. Isolating them can be done by having the radicals on opposite sides of the equation, which will then get simplified further when we square both sides.
It is also important to note before solving for the variable “x”, that we just came from squaring both sides. The equation that follows can then either be a straightforward linear equation or a more challenging quadratic equation.
With these guidelines, solving equations become far less intimidating and can even become an interesting puzzle to solve.
Expressions and Equations Work with radicals and integer exponents.
CCSS.MATH.CONTENT.8.EE.A.2
Transcript Solving Radical Equations
Leo Vitruvian, the polymath, is good at many things. He's an inventor, a painter and quite the mathematician. A local banker, Lorenzo Medici, has asked Leo to create the world's first flying machine. Lorenzo would like Leo to paint the propellers in the colors of his family's crest, so he gives Leo some special instructions, which he delivers on a scroll, of course. To complete the task correctly, Leo must be able to solve radical equations.
Leo Vitruvian goes down to his local paint shop in search of the special palette of paints. There are so many colors! It’s like a color library! Let’s take a closer look at Leo Vitruvian’s instructions. No! The paint shop has a different labeling system! The shop owner looks utterly confused.
Isolating the radical
Starting with the first equation, we have the square root of 'x', plus 6, equals 9. When solving radical equations, it's good to first try and isolate the radical. Here, we use opposite operations to isolate the square root of 'x'. Next, we square both sides, giving us our answer, 9. Leo Vitruvian can safely purchase this color.
The other equations don’t look so simple. The next color on the list is 4 equals 2 root quantity 'x' over 3. Even though this equation looks different, let's see if following our checklist still works. First, we isolate the radical by dividing both sides by 2. Next, we square both sides - just like before. And finally, we isolate the 'x' using opposite operations. Leo Vitruvian adds this color to his basket as well.
Equations with two Radicals
The next equation is uh oh Leo's in trouble...two radicals?! One on each side?! It's going to be hard to isolate these radicals, so let's just square both sides and get rid of them. That's looking a whole lot better! Now just solve by using PEMDAS!
These equations just keep looking messier and messier. But Leo sticks with his checklist. ‘x' equals the square root of the quantity 2x plus 8. The radical is already isolated, so he must have to square both sides to get rid of the radical. This equation looks familiar. Leo must've used it in another painting he did for Lorenzo. Leo Vitruvian recognizes that he can put this quadratic equation into standard form. Then he'll have several ways to solve it! Leo goes for factoring, since the numbers are playing nice. He finds the solution and adds this color to his basket.
With all the colors selected and purchased, Leo Vitruvian goes to paint the flying machine. He’s just putting on the final touches. Time to test!
Solving Radical Equations exercise
-
Help Leo recall how to solve his radical equations.
HintsFor each equation, you have to square once.
Use opposite operations. For example:
$\begin{array}{rcl} x+4&=&~9\\ \color{#669900}{-4} & &\color{#669900}{-4}\\ x&=&~5 \end{array}$
Check your solutions by putting them in the original equations.
SolutionLet's start with the first equation Leo Vitruvian has to solve: $\sqrt x+6=9$.
To solve $\sqrt x+6=9$ first subtract $6$ to get $\sqrt x=3$. Next square both sides of the equation to get the solution $x=9$.
The next equation looks a little more difficult: $4=2\sqrt{\frac x3}$.
Again we first transform the equation in such a way that we eventually have to square both sides of the equation:
$\begin{array}{rcl} 4&=&~2\sqrt{\frac x3}\\ \color{#669900}{\div 2} & &\color{#669900}{\div 2}\\ 2 & = & ~\sqrt{\frac x3} \end{array}$
Now we have to square to get $4=\frac x3$, and then multiply by $4$ to get $x=12$.
The last equation is $\sqrt{5x-11}=\sqrt{x+9}$.
Because we have a square root on both sides we first have to square both sides to get $5x-11=x+9$. This is a well known linear equation which we solve by using opposite operations:
$\begin{array}{rcl} 5x-11&=&~x+9\\ \color{#669900}{+11} & &\color{#669900}{+11}\\ 5x&=&~x+20\\ \color{#669900}{-x} & &\color{#669900}{-x}\\ 4x&=&~20\\ \color{#669900}{\div 4} & &\color{#669900}{\div 4}\\ x&=&~5 \end{array}$
-
Find the right color for $x=\sqrt{2x+8}$ by solving for $x$.
HintsTo check the factorization use the FOIL method for multiplying two binomials:
F multiply the first terms.
O multiply the outer terms.
I multiply the inner terms.
L multiply the last terms.
A product equals zero if one of its factors equals zero.
To solve the equation for each factor use opposite operations.
SolutionLets solve $x=\sqrt{2x+8}$ so that we can figure out which color it belongs to.
We have a square root on the right side and the variable $x$ on both sides.
We still have to square first:
$x^2=2x+8$.
If we subtract $2x$ as well as $8$ on both sides we get a quadratic equation
$x^2-2x-8=0$.
Using the FOIL method we can confirm that $x^2-2x-8=(x-4)(x+2)$. so we get the following equation:
$(x-4)(x+2)=0$.
With the zero factor property we can conclude that either
$\begin{array}{rcl} x-4 & = & ~0\\ \color{#669900}{+4} & &\color{#669900}{+4}\\ x& = & ~4 \end{array}$
or
$\begin{array}{rcl} x+2 & = & ~0\\ \color{#669900}{-2} & &\color{#669900}{-2}\\ x& = & ~-2 \end{array}$
Be careful... if you check your solutions you get the following:
- $4=\sqrt{2\times 4+8}=\sqrt{16}$ $~~~~~$✓
- $-1=\sqrt{2\times (-1)+8}$ can't be true because a square root is always positive.
-
Solve the radical equations.
HintsKeep in mind to square once.
You first might have to isolate the square root.
It is always a good idea to check your solutions.
Let's have a look at an example:
$\sqrt x-3=3$.
Adding $3$ leads to $\sqrt x=6$. Next we square both sides to get $x=36$.
Checking the solution:
$\sqrt{36}-3=6-3=3$ $~~~~~$✓
SolutionKeep in mind that you have to square both sides to solve radical equations. If necessary, after isolating the square root. Let's have a look at the equation we have to solve:
$\sqrt{2x}-1=3$
- First we have to add $1$ to both sides to get $\sqrt{2x}=4$.
- Next we can square both sides to get $2x=16$.
- Lastly we divide by $2$ to get the solution $x=8$.
- Here we can square both sides immediately to get $2x-1=9$.
- Now we have a linear equation we solve by using opposite operations: adding $1$ to $2x=10$ and dividing by $2$ to get the solution $x=5$.
- Adding $1$ leads to $2\sqrt x=4$.
- Dividing by $2$ gives us $\sqrt x=2$.
- Lastly we square to get the solution $x=4$.
- Dividing by $2$ leads to $\sqrt{x-1}=1.5$.
- Now we square to get $x-1=2.25$.
- Lastly we add $1$ and get the solution $x=3.25$.
-
Color in the different parts of the uniform with the right colors.
HintsFirst isolate the square root if necessary.
If the square root is isolated, you can square both sides.
Perhaps you have to use opposite operations to solve the resulting equation.
Check your solutions by putting them in the origin equations.
SolutionLet's help Magnus find the right colors by helping her solve the radical equations she has been given:
$~$
$\sqrt{2x+5}-2=1$
- Add $2$ to get $\sqrt{2x+5}=3$.
- Now square both sides to get $2x+1=9$.
- Subtracting $1$ and dividing by $2$ after gives the solution $x=4$.
$~$
$\sqrt{x+4}=\sqrt{2x-1}$
- Here we square both sides directly and get a linear equation $x+4=2x-1$.
- We solve this equation using opposite operations: subtracting $x$ and adding $1$ after to get the solution $x=5$.
$~$
$2\sqrt{x}-3=1$
- Pay attention to PEMDAS: first add $3$ to get $2\sqrt x=4$ and divide by $2$ after to get $\sqrt x=2$.
- Lastly square to get the solution $x=4$.
$~$
For the last part we have to solve the equation $\sqrt{x+3}=\sqrt{4x}$.
- Squaring on both sides leads to the linear equation $x+3=4x$.
- Now subtract $x$ to get $3=3x$ and divide by $3$. The solution is $x=1$.
-
Explain how to solve radical equations.
HintsThe equation $x+2=2x-3$ is a linear equation.
Subtracting $x$ and adding $3$ leads to $x=5$.
Checking this solution, we see that
$5+2=2\times 5-3$ $~~~~$✓
We always use the opposite of the given operation:
$\begin{array}{rcl} x+ 2 & = & ~2x-3\\ \color{#669900}{-x} & &\color{#669900}{-x}\\ 2 & = & ~x-3\\ \color{#669900}{+3} & & \color{#669900}{+3}\\ 5 & = & ~x \end{array}$
The opposite operation of a square root is squaring.
SolutionA radical equation is characterized by a square root. The opposite operation of a square root is squaring.
Let's have a look at an example: $\sqrt x=2$ leads to $x=4$ by squaring.
So no matter what you have to square to get rid of a square root. But you can only do this if the square root is isolated. Otherwise you have to use opposite operations. For example:
$\begin{array}{rcl} \sqrt x+6 & = & ~9\\ \color{#669900}{-6} & &\color{#669900}{-6}\\ \sqrt x & = & ~3 \end{array}$
Now you can square again.
Sometimes squaring leads to further equations, for example linear equations. You still have to use the methods you've already learned, like opposite operations, to solve these kinds of equations.
-
Calculate the solutions to the given radical equations.
HintsFirst isolate the square root, then square both sides.
Squaring the equation $\sqrt{2x+3}=x$ leads to two solutions. If you check the two solutions, you will see that one of them actually fails.
Solve the resulting equations using opposite operations.
It's always better to check your solutions.
SolutionLet's start with $3+\sqrt x=5$. First we subtract $3$ to get $\sqrt x=2$. Squaring gives us the solution $x=4$.
Next we have an equation with one point to take care of: $\sqrt{2x+3}=x$.
- Squaring both sides leads to $2x+3=x^2$.
- Next we divide by $2x$ as well as $3$ to get $x^2-2x-3=0$.
- Now we factor the left side to get $(x-3)(x+1)=0$.
- Using the zero factor property, we get that $x=3$ or $x=-1$.
- $\sqrt{2\cdot 3+3}=\sqrt 9=3$ $~~~~~$✓ This is the desired solution.
- $\sqrt{2\cdot (-1)+3}=\sqrt 1=1\neq -1$. This solution doesn't satisfy the equation.
Now consider $2\sqrt x+2=4$
- Subtract $2$ to get $2\sqrt x=2$.
- Divide by $2$ to get $\sqrt x=1$.
- Squaring gives us the solution $x=1$.
Finally, $\sqrt{2x-5}=\sqrt{3x-12}$
- Squaring first gives the linear equation $2x-5=3x-12$.
- Subtracting $2x$ and adding $12$ lead to the solution $x=7$.