Shares in Division

Basics on the topic Shares in Division
Shares in Division
Imagine your class is helping out at a space racer factory. How exciting! But oh no, what is that sound? The distributer machine broke down during production! Not to worry: Your class can help so that each space racer is built on time. In order to do that, you need to do equal groups division to distribute materials between the space racers. Can you finish the division with equal groups problems and ensure the building of the space racers? The following text gives you some guidance in how to use shares in division.
How to Do Division as Equal Groups
To do division as equal groups, you need to follow these steps:
| Step # | What to do |
|---|---|
| 1 | Identify the divisor for the number of groups needed. |
| 2 | Identify the dividend for the number we need to distribute equally. |
| 3 | Share the dividend equally into each group until none remain. |
| 4 | Count the objects in one group to find the quotient. |
Shares in Division – Example
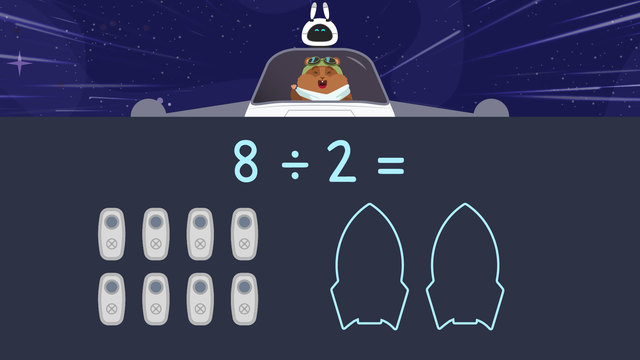
To begin, we see that we have eight doors that need to be shared equally between two space racers.
This means our divisor is two and our dividend is eight:
First, we set up two groups to match our divisor:
Next, set up eight objects to match the dividend, ready to be shared:
Then, share all objects into each group equally until no more objects remain:
Finally, look at one of the groups and count the objects inside. Inside one of the groups, we see four objects, so the quotient is four. Eight can be shared into two equal groups of four:
Congratulations, you figured out how to build the space racers in time!
Shares in Division – Summary
Remember, if you want to share equally, you need to do equal groups division.
If you want to solve equal group problems, you should follow these steps:
- Identify the divisor for the number of groups needed.
- Identify the dividend for the number we need to distribute equally.
- Share the dividend equally into each group until none remain.
- Count the objects in one group to find the quotient.
For further practice, you will find some division with equal groups worksheets for 3rd grade next to the text.
Transcript Shares in Division
Mr. Squeaks and Imani have been summoned to the Space Racer Factory. The factory has run into a big problem. The distributor machine broke down during production. Mr. Squeaks and Imani have been assigned to help distribute materials into equal groups, so each space racer can be built on time. To do this, they will need to use shares in division. When we set up a division problem, we have the dividend, divisor, and the quotient. The dividend is the largest number that is being shared equally. The divisor is the number of groups we have and the quotient is the total number in each group. When we use equal shares in division, we are distributing objects equally into groups. To do equal shares, first identify the divisor for the number of groups needed. Next, identify the dividend for the number we need to distribute equally. Then, share the dividend equally into each group until none remain. Finally, count the objects in one group to find the quotient. Let's practice before you help Mr. Squeaks and Imani. The factory has eight doors to be shared evenly between two space racers. We can write this as eight divided by two. This is our dividend, and here is our divisor. Set up two groups like this to represent the divisor. The dividend is eight, so share it between the two groups, until all objects have been distributed equally. To find the quotient, look at one of the groups and count the total objects in the group. This group has four doors, so the quotient is four. We can restate this by saying eight shared into two equal groups of four. The two space racers get four doors each. Now we know how to share equally into groups, let's help Mr. Squeaks and Imani! There are twelve thrusters to be shared between six space racers. We can write this as twelve divided by six. How many groups do we need? The divisor is six, so set up six groups. How many objects are we distributing equally into each group? We are distributing twelve objects equally into each group, so we begin sharing between the six groups, until all objects are distributed equally. How do we find our quotient? We look at one group and count how many objects are in it. This group has thrusters, so our quotient is two. We can restate this by saying twelve shared into six equal groups of two. The six space racers get two thrusters each. Now for the final problem. There are fifteen windshields that need to be shared between five space racers. What is the division sentence? It is fifteen divided by five. How many groups are needed? The divisor is five, so set up five groups. How many objects are we sharing equally into groups? The dividend is fifteen, so we are sharing fifteen objects equally into each group. We begin sharing fifteen between the five groups until everything has been distributed equally. How do we find our quotient? Look at one group and count the objects inside. This group has three windshields, so the quotient is three. We can restate this by saying fifteen shared into five equal groups of three. The five space racers get three windshields each. Mr. Squeaks and Imani have completed their assignment. Remember, to do equal shares in division, first identify the divisor for the number of groups needed. Next, identify the dividend for the number we need to distribute equally. Then, share the dividend equally into each group until none remain. Finally, count the objects in one group to find the quotient. It looks like this space racer is ready for testing. Hang on a second, it's Mr. Squeaks and Imani. "Imani, this is awesome! Yeehaw!"
Shares in Division exercise
-
Match the problems and answers.
HintsFirst look at the divisor. This is the number of groups needed.
The divisor is represented by rockets in each image.
Next look at the dividend this is the largest number in the equation that tells us how many we need to distribute evenly.
The dividend is represented by the windows in each image.
Look at the equation. Then count how many windows are in each rocket. Your answer is the number of windows in 1 rocket.
SolutionThe dividend represented by the rocket windows tell us the number that needs to be shared out equally.
The divisor represented by the rockets tell us the number of groups we need to share by.
When the divisor has been shared equally by the dividend we look at one of the groups and get our answer.
16 $\div$ 4 = 4
8 $\div$ 4 = 2
10 $\div$ 2 = 5
12 $\div$ 4 = 3
-
Can you help Mr Squeaks by ordering the steps?
HintsWhat must we identify first?
Remember the divisor tells us the amount of groups needed. The dividend tells us the number we need to distribute evenly.
SolutionFirst we look at the problem as a whole.
Identify the divisor
Identify the dividend
Share the dividend equally into each group.
Count the objects in one group to get your answer.
-
Can you help Mr Squeaks and Imani solve the division problem?
HintsIdentify the divisor. This tells you how many groups are needed.
Then you need to identify the dividend. This tells you the number you need to distribute equally.
Check each image to see which one is showing the same divisor. The rockets are representing the divisor by showing how many groups are needed.
Check the images to see which ones are showing the same dividend. The windows are representing the dividend.
Solution24 $\div$ 6 = 4
24 windows have been divided equally between 6 rockets.
There are 4 windows in each rocket.
-
Can you help Imani distribute the lightsticks?
HintsCheck your calculation. What is the divisor? Remember this is the number of groups needed.
What is the dividend? This will be the largest number as it tells you the number that needs to be distributed evenly.
The answer is the number in each rocket.
SolutionThe divisor shows the number of groups there are.
The dividend is the total number (lightsticks) that need to be divdided.
The answer is the number of lightsticks in each rocket.
-
Can you help workout how many seatbelts are needed for each rocket?
HintsRemember identify the divisor.
The divisor is the number of groups needed.
The divided is the total number of objects that need to be shared. This is the largest number in the calculation.
Solution16 $\div$ 4 = 4
There were 16 seatbelts in total and 4 rockets. When the seatbelts where shared evenly, there were 4 seatbelts in each rocket.
-
Can you help Mr Squeaks and Imani solve the division problems?
HintsYou may want to get a pencil and paper to help. Start by drawing a rocket for the quantity labelled in the divisor . Then start by dividing the dividend equally.
12 $\div$ 4 =
You could draw 4 rockets or circles.
Then share out 12 amongst the rockets or circles.
Look at the divisor. This is how many groups you need.
Look at the dividend. This is the larger number that you need to share out equally between the divisor (groups).
Solution8 $\div$ 2 = 4
15$\div$ 5 = 3
20 $\div$ 4 = 5
18 $\div$ 3 = 6


















